水下冲击波作用下双层壳结构响应特征研究

古 滨,李炳南,姚熊亮,王志凯

(1.西华大学 土木建筑与环境学院，成都 610039；2.哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

舰船非接触水下爆炸通常引起船体剧烈的振动和较大的塑性变形，导致船上各类的重要设备广泛的冲击破坏及舰船总体结构的破损，使舰船失去战斗力[1]。

水下武器的威胁是舰船生命研究的重点，水下武器主要有水雷和鱼雷，命中舰船的形式有接触和非接触，不同爆距对舰船的损伤效果也不相同。对于中远场的非接触水下爆炸而言，需要考虑冲击波载荷、气泡脉动载荷，以及它们与舰船结构的相互耦合作用[2]。

圆柱壳是潜艇与海洋工程结构物中广泛采用的结构单元，研究圆柱壳结构在水下爆炸作用下的结构响应特征对于进一步分析圆柱壳结构的失效规律和机理非常重要。在该领域内，已有一些研究成果发表，周游等[3]系统分析了不同装药设置条件下圆柱壳爆炸变形模式特征，得到了圆柱壳的屈曲变形历程，关键单元压力时程曲线和迎爆点的位移、应力和速度时程曲线。邵宗战[4]开展了水下爆炸作用下圆柱壳周围压力场分布的研究。冯彤晖等[5]采用RAVS方法建立理论模型及其在水下爆炸冲击的运动微分方程组，讨论分析了不同药量下覆盖层厚度、肋骨间距和爆距等因素对径向加速度峰值的影响。Tally等[6]对两层同心圆柱壳在远距离水下爆炸强击波作用下的动态响应进行了研究。姚熊亮等[7-9]开展了改变外壳板厚和内壳板厚对结构各部分的冲击响应研究、加肋双层圆柱壳冲击响应的仿真研究、结构参数变化对双层圆柱壳冲击响应的研究。

随着近年来数值仿真技术的发展，国际上陆续出现了很多大型有限元动力分析软件(例如ABAQUS、ANSYS/LS-DYNA等)，通过有限元软件模拟分析舰船冲击响应成为切实有效的方法。

数值模拟舰船爆炸冲击响应问题，已有不少研究成果[10-12]，如姚熊亮等[13]结合LS-DYNA，分析了不同水下非接触爆炸时,水面舰船船底结构冲击加速度峰值随排水量等参数变化的趋势，为水面舰船生命力评估提供了一种便捷的输入冲击环境。张振华等[14]提出了一个利用MSC /DYTRAN数值模拟水面船舶在远距离水下爆炸载荷作用下动力响应的方法。贾则等[15]采用Hypermesh软件建立流场和全船的计算模型，利用ABAQUS软件对水下爆炸后大型舰船的冲击响应进行数值模拟，并比对理论计算分析结果，验证了数值计算分析的有效性。姚熊亮等[16]采用有限元分析软件ABAQUS中的声固耦合算法对舰船几种典型的水下爆炸模型进行了计算和分析，并将数值模拟结果与实测数据进行对比分析，验证了数值计算分析精度较高。朱锡等[17]以加筋圆柱壳模型为分析对象，应用MSC-DYTRAN非线性瞬态有限元分析软件建立水下爆炸载荷作用下流固耦合数值分析模型，分析了加筋圆柱壳在爆炸载荷作用下的破坏机理。侯海量等[18]建立了战斗部近距爆炸下夹芯复合舱壁结构防护能力的理论评估模型，提出了联合作用下夹芯复合舱壁结构的防护能力需同时满足抗弹性能和整体变形破坏两方面的要求。

双层壳体结构被广泛应用于水面舰船的双层底或潜艇的轻外壳设计中，近年来随着人们对舰船抗爆抗冲击问题的重视，双层壳体结构对舰船的抗水下爆炸能力的影响问题也受到更多关注。早期公开发表的文献较少，且局限于冲击波本身的透射特性和内部流体的简化处理方法。本文将水面舰艇的双层壳结构作为数值模拟的目标，使用LS-DYNA有限元数值模拟软件，并结合ALE方法建立了水下爆炸载荷与双层壳结构的强冲击耦合计算模型，随后将计算模型导入有限元分析软件LS-DYNA中，数值模拟水下爆炸后结构的冲击响应，以获得壳体周围的冲击波压力特征，以及不同舷间介质及水深条件下的结构响应特征；并考察数值模拟获得的不同位置壳体的响应规律与理论计算分析结果的相符性，以期为航行器的结构设计提供参考。

1 数值计算方法

1.1 ALE算法

ALE算法常用于模拟大变形问题和流固耦合问题，ALE算法是由Lagrange算法和Euler算法发展而来。具备Euler算法与Lagrange算法的各自的长处，同时克服了两种算法的不足之处。因此ALE算法是目前解决近场水下爆炸流固耦合问题最有效的方法。

Euler算法(其基本原理如图1所示)是基于Euler空间描述是以整体坐标系为基础，结构和空间属于分离状态，结构在空间网格中运动，空间网格固定不变。因此，Euler算法适合用于大变形问题，尺寸形状固定的欧拉网格能保证计算迭代步不变。Euler计算主要包括两部分：(1)结构材料网格变形；(2)结构材料网格在在欧拉域中划分传递。

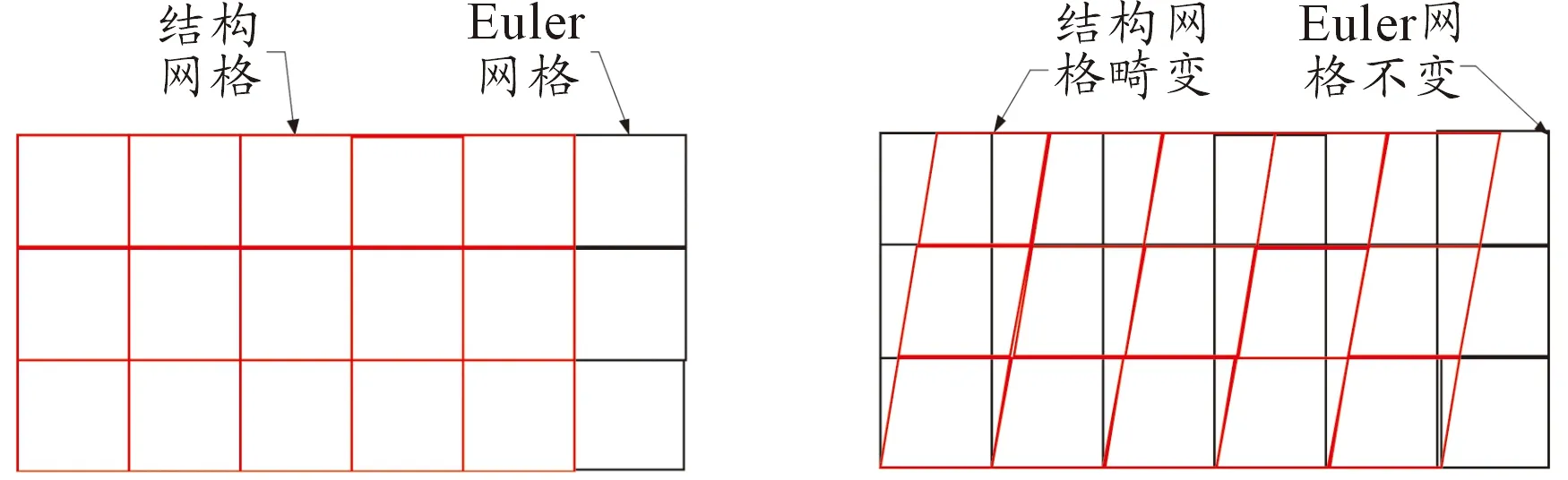
图1 Euler法基本原理

Lagrange算法(其基本原理如图2所示)是基于自然坐标系，坐标系随着质点运动而运动。因此拉格朗日方法适合精确描述实体结构的边界运动特征。但是在处理大变形问题时，畸变网格会降低计算精度，严重时导致错误，无法计算。

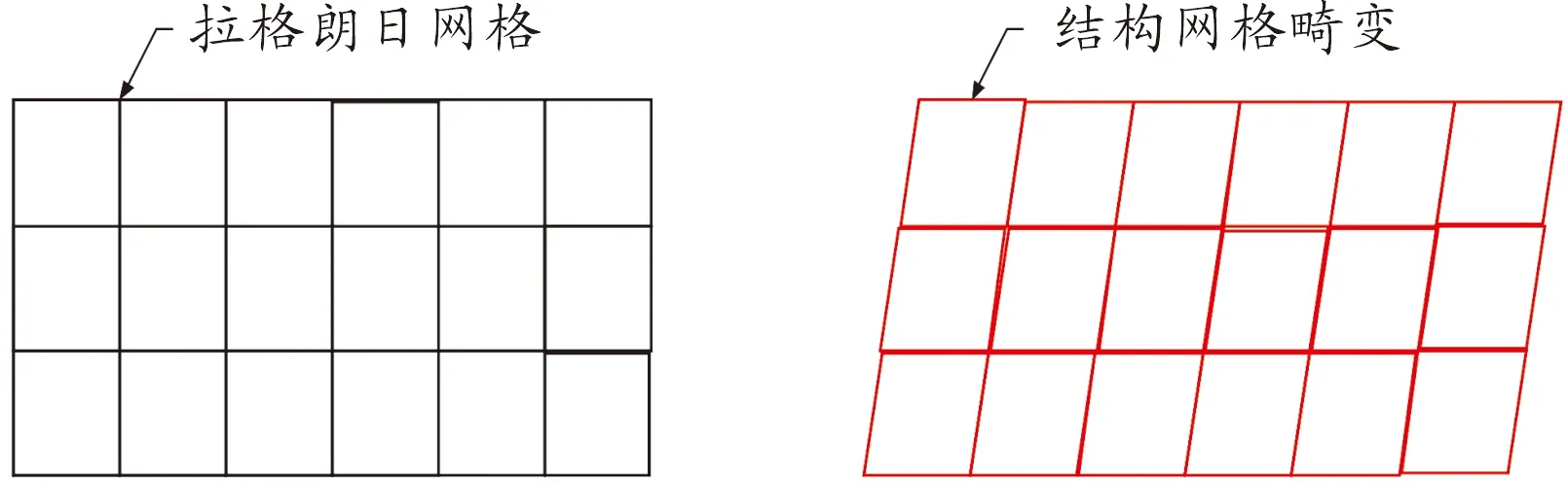
图2 Lagrange法基本原理

因此，ALE算法(其基本原理如图3所示)兼具Euler算法和Lagrange算法的优势，ALE描述引入了一个可以独立运动的构型。在弹性体变形过程中，坐标始终随构型运动引入坐标，网格构型可以是任意给定的，记网格变形速度为v。当v不等于0时，网格在空间独立运动，对应于通常的ALE方法；当v等于0时，网格在空间位置不动，退化为欧拉描述；网格与弹性体一起运动退化为拉格朗日描述。基于以上特点ALE方法能够精确追踪材料边界的运动同时保持了Euler网格的特点，而且能够自适应调整位置。因此ALE方法的计算速度相较于传统Euler方法有明显提高，同时保持了材料边界变形的精确描述。

ALE算法在计算过程中首先按照拉格朗日算法执行计算几个分析步，结构网格产生位移或者变形，然后执行ALE计算分析步，进行单元网格的重新划分并且将各个变量输出重新映射到新的单元网格中。

图3 ALE法基本原理

1.2 ALE算法的动力学描述

ALE描述中，除了独立构型与现时构型外还另外引入了一个参考构型。在质点运动过程中，观察者随着参考构型运动，而初始构型和现时构型都相对参考构型运动。从随质点运动的自然坐标系来描述参考构型中各个点的位置为：

ζ=ζ(X,t)

(1)

而从相对于Euler空间点的整体坐标系来描述则为：

ζ=ζ(x,t)

(2)

式(1)与式(2)中为参考构型中的各个点的位置矢量。

通过位移矢量的微分可以得到速度矢量的表达式。因此，空间中质点X的运动速度可以表示为

(3)

同理，参考构型中某点ζ在空间中的运动速度v′可以表示为

(4)

质点X在参考构型坐标系中的运动速度v″可以表示为：

(5)

在ALE描述中，物理量采用参考构型进行描述，相应的各个物理量的物质导数可以通过其参考倒数来计算得到，对x求物质倒数，得：

(6)

式(6)可以变形为：

(7)

(8)

根据式(7)可以把各物理量F(ζ,t)表达为现面的统一表达形式：

(9)

2 数值模型与验证

双层壳结构是常规潜艇常用结构，在潜艇上体现为耐压壳与非耐压壳两层结构。在非耐压壳结构包括非耐压水密结构和非耐压非水密结构。非耐压水密结构不用制造成耐压结构是因为潜艇下潜时，非耐压水密结构会与舷外水相通，这样这部分结构在水下时内外压力相等。非耐压非水密结构更多作用在于保护内部结构与改变外形功能。

对水下圆柱壳模型在爆炸载荷作用下的响应特点进行有限元仿真计算，模型采用双层圆柱壳与流场耦合模型进行计算。外层圆柱壳直径1.1 m，内层圆柱壳直径0.9 m，板厚为10 mm，圆柱壳体长1.35 m。圆柱壳材料为235钢，密度ρ=7 800 kg/m3，弹性模量E=205 GPa，泊松比0.3。壳体内部为空气。爆距设置为0.4 m。计算模型如图4、图5所示。

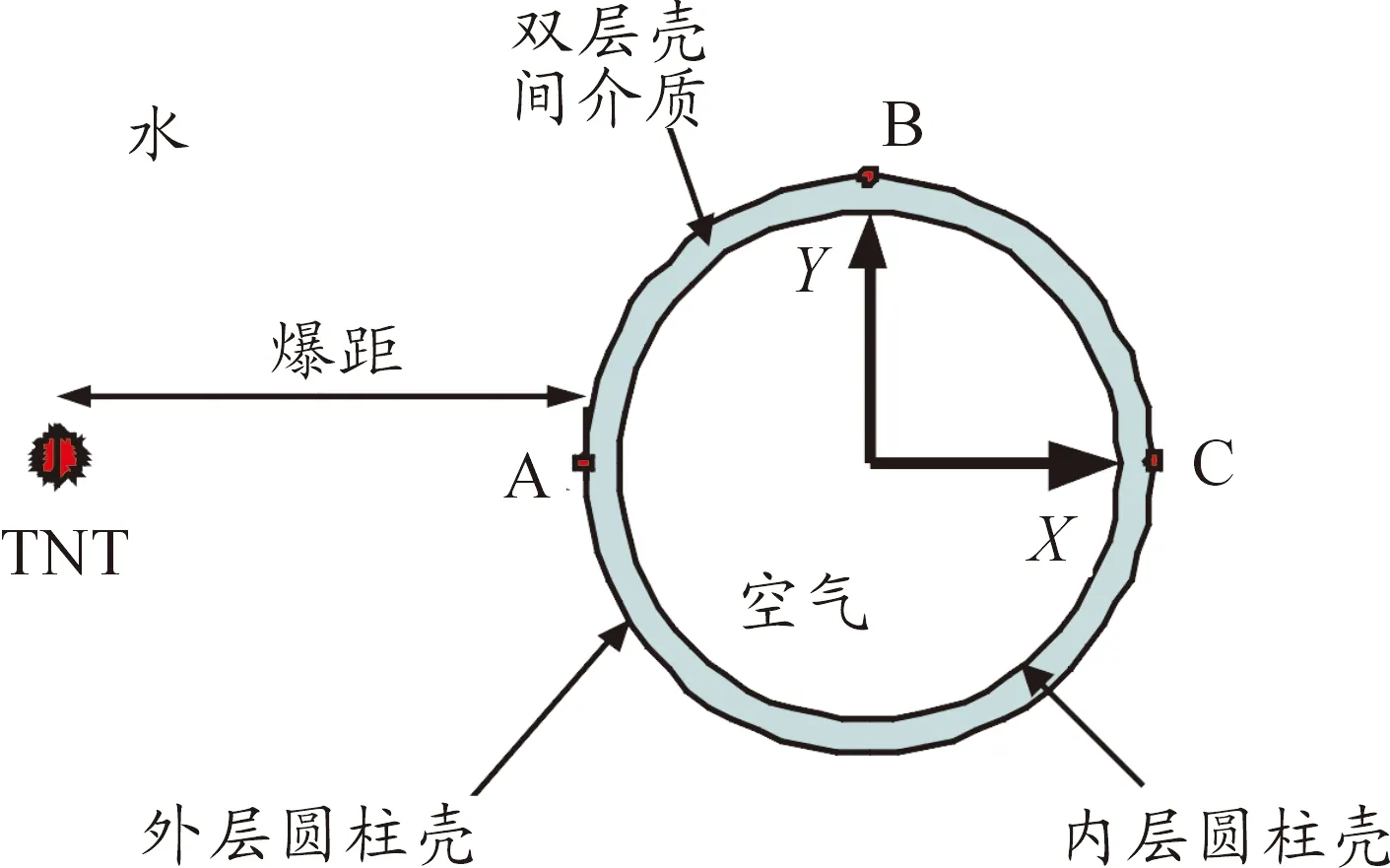
图4 模型示意图

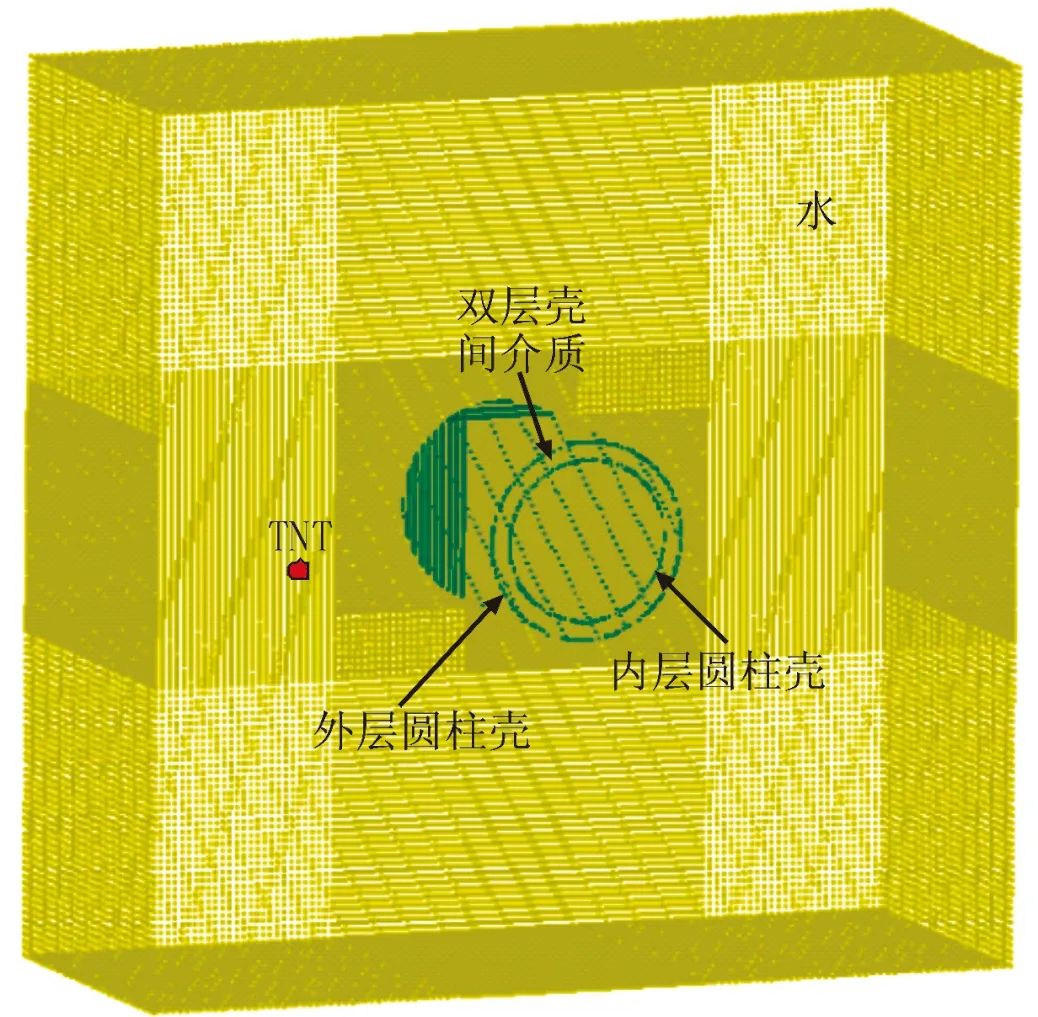
图5 有限元计算模型

提取爆心不同距离的单元压力时间曲线结果如图6所示，利用第一节中对爆炸载荷的理论计算公式进行理论求解，理论数据结果如图7所示。

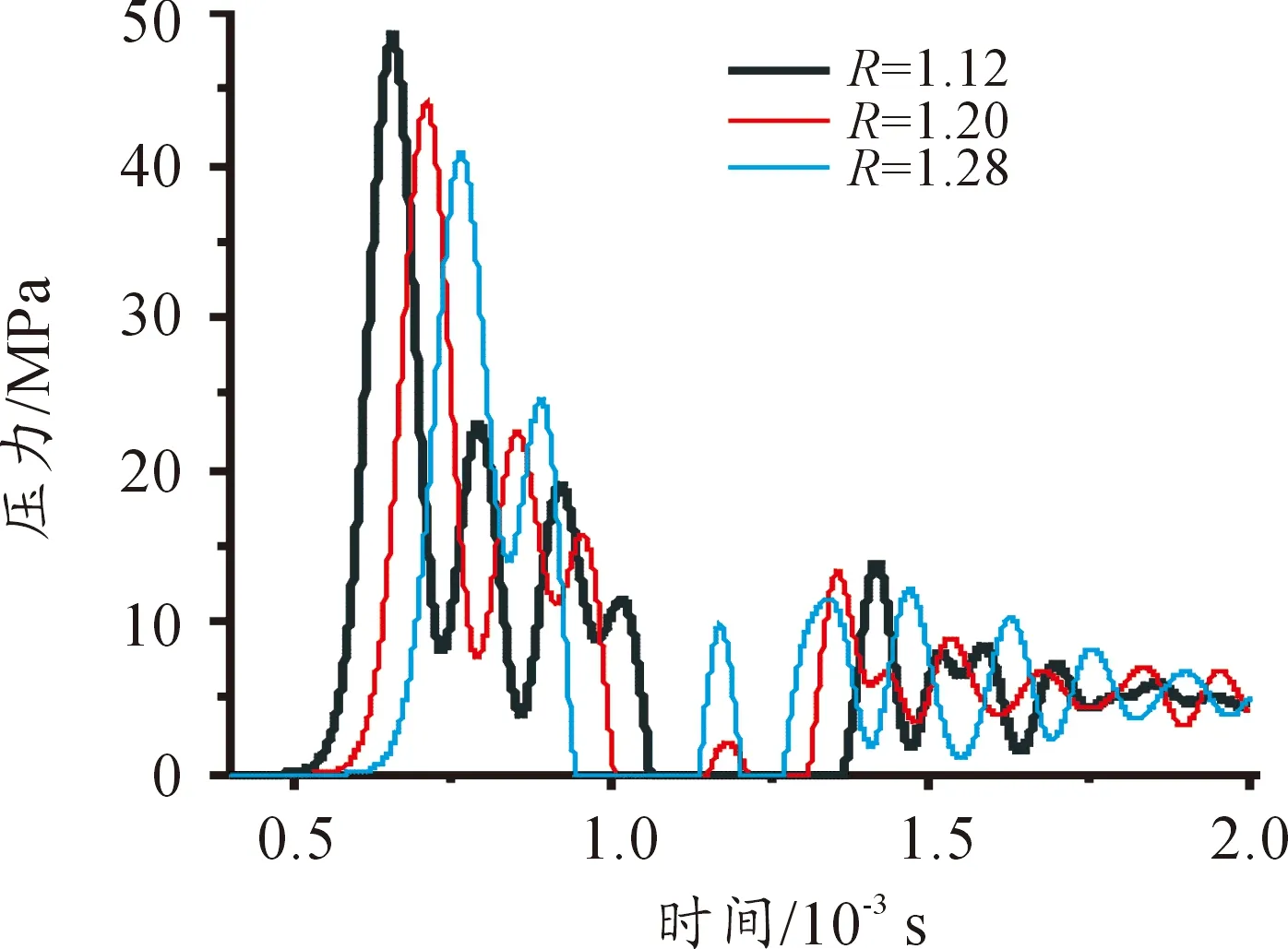
图6 LS-DYNA仿真计算结果

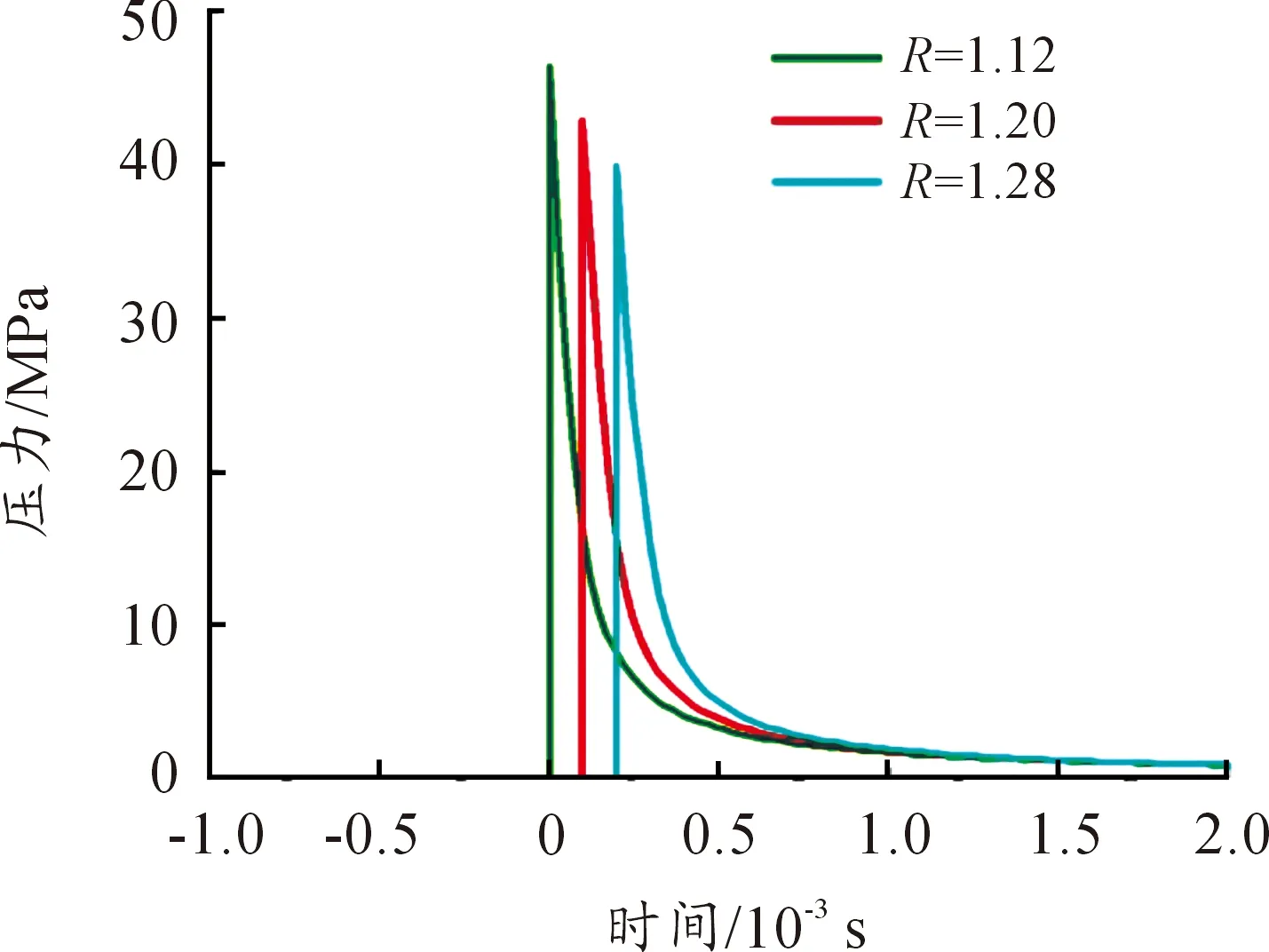
图7 理论公式计算结果

两种计算方法中得到的三点第一个压力峰值数据如表1所示。

表1 两种计算方法压力峰值数据

通过表格中数据结果表明，当爆距为1.12 m时，通过模型计算的结果与由经验公式得出的结果之间的误差为4.3%；当爆距为1.2 m时，误差为2.7%；当爆距在1.28 m时，误差为2.2%。三组计算结果的最大误差为4.3%。结果表明，该计算模型中各材料参数与网格大小选择正确，计算结果偏差小，后续计算过程可以应用该模型与网格尺寸。

3 结果与分析

3.1 壳体周围的冲击波压力特征

利用上述模型，将双层壳间介质分别设置为水与空气。药包质量设置为1 kg。压力测点布置如图8所示。

图8 测点布置示意图

爆炸载荷在水中传播到作用于圆柱壳的过程如图9所示。

在t=2.4 ms时，冲击波压力到达外圆柱壳形成反射波，同时冲击波在空气介质圆柱壳时，冲击波没有作用于内圆柱壳形成透射压力波。在冲击波作用于水介质圆柱壳外壳时，冲击波通过外圆柱壳透射作用于内圆柱壳结构，背水板与背空板透射系数存在极大差异；在t=10.5 ms时，冲击波已经越过圆柱壳结构最高点，绕射冲击波向圆柱壳后方传播。空气介质双层壳结构反射波高压区域明显要比水介质双层圆柱壳结构反射波高压区域大，且空气介质圆柱壳背爆面的绕射压力区域范围与压力值均大于水介质双层圆柱壳；在t=12 ms时，冲击波已经完全越过圆柱壳结构，绕射压力波在圆柱壳背爆面汇合，并且向更远处继续传播。提取结构周围的水压如图10～图12所示。

图9 爆炸载荷在水中传播到作用于圆柱壳的过程

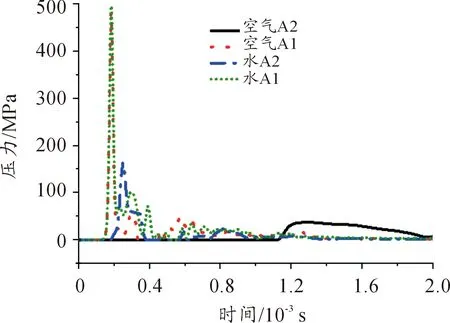
图10 迎爆面载荷时历曲线

图11 背爆面载荷时历曲线

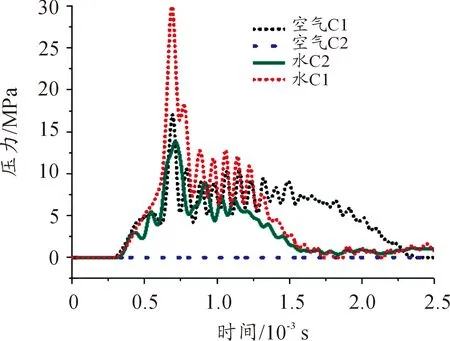
图12 圆柱壳最高点载荷时历曲线

迎爆面背空板与背水板测点A1的冲击波第一个峰值相等，此时只有纯粹的入射压力能量，等爆距、等TNT当量条件下峰值相等。第二个峰值处两种不同介质的圆柱壳测点A1压力发生了差异，背水外圆柱壳的压力为100 MPa，而背空外圆柱壳的压力为50 MPa，两种不同介质的圆柱壳反射率存在明显差异。冲击波在水介质双层壳结构间不停地来回反射形成振荡。空气介质则不存在此类现象。A2测点的压力值曲线对比可以看出水介质圆柱壳和空气介质圆柱壳压力值存在极其明显的差值，空气介质内圆柱壳的外壁压力值基本为零，水介质内圆柱壳的外壁压力为16 MPa，是外壁压力的0.32倍；水介质圆柱壳与空气介质圆柱壳背爆面外壁周围水域测点B1压力值分别为8 MPa、5.1 MPa。对比两载荷的脉宽，背空圆柱壳明显大于背水板。内圆柱壳结构周围的压力测点B2的压力值同样因为水与空气的阻抗系数差异，空气压力几乎为零；圆柱壳最高点测点C1处外壁周围压力已经存在很大差异性，背空圆柱壳的压力峰值已经远小于背水板C1处压力值。同时背空板外壁压力衰减速度明显小于背水板结构。

3.2 水深条件对冲击波载荷传播的影响

本节对潜艇活动的不同水深爆炸载荷作用的特性进行分析对比，探究不同水深条件下载荷的特性与结构响应特性。水深设置五种工况，分别为20 m、100 m、200 m、300 m。

选取4个水深状态下冲击波传播过程中的几个时刻点，描述冲击波的传播过程如图13所示。

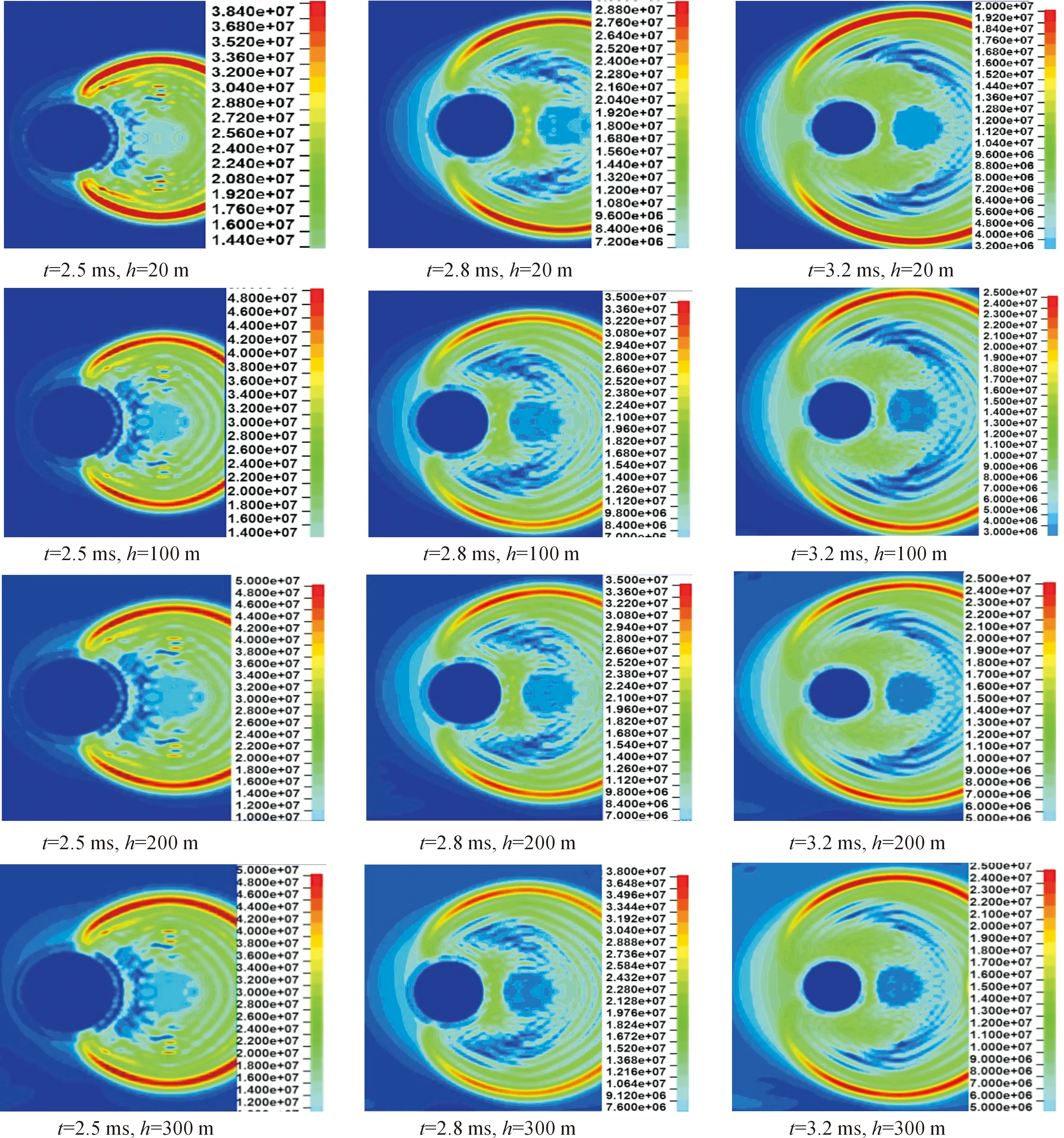
图13 冲击波传播过程

冲击波在t=2.5 ms时到达圆柱壳最高点，冲击波超压峰能量在圆柱壳遮挡区域被圆柱壳吸收并且形成透射反射，因此水中的压力值相对无阻碍区域要小；在t=2.8 ms时，冲击波开始向圆柱壳背爆面绕射；t=3.2 ms时冲击波已经越过圆柱壳开始远离，同时从圆柱壳上下两边绕射的波在背爆面汇聚，形成高压。

提取迎爆面、背爆面以及圆柱壳最高点周边水域中的压力时间曲线，结果如图14所示。

图14 压力曲线

C1点的压力曲线表明4个水深条件下，冲击波峰值不存在差异性，冲击波传播时间与峰值在20 m到300 m水深区间均一致。峰值过后的震荡过程是由于圆柱壳的反射压力与入射压力相互作用形成。C2点的压力时间曲线与C1点的曲线趋势一致，只是，峰值存在很大差异，透射系数为0.56。在t=4.7 ms时，入射压力形成第二个压力峰值，是由于A点入射压力导致内压增加进而导致整体压力增大。B1点与B2点的压力曲线趋势一致，且在3 ms时存在明显的压力峰值。这是背爆面受到绕射作用形成。综上所述，冲击波载荷压力波动规律在不同水深基本无差异性。四个水深下的压力曲线表明，水压差别是曲线差异性的主要原因。

3.3 壳体响应特征

如图15所示为双层圆柱壳结构上的压力云图。

在t=2.5 ms时，背空板与背水板的外圆柱壳压力值存在明显差异，背空板的压力峰值要大于背水板的压力值；在t=4 ms时，背水板的外壳压力值通过舷间水透射到内圆柱壳。背空板的外圆柱壳压力则没有透射压力作用于内圆柱壳，由于能量没有其他结构吸收消耗，背空板的外圆柱壳压力值明显大于背水板的外圆柱壳结构的压力值；在t=5 ms时，两种不同介质的圆柱壳结构压力分布已经差异明显，水介质圆柱壳结构中的压力波透过舷间水作用，压力波能量由外壳分散至内壳的峰值小于背空板结构的峰值。

如图16所示为双层圆柱壳结构与单层圆柱壳结构在相同载荷作用下的壳体表面压力分布图。在t=2.5 ms时，爆炸冲击波作用在圆柱壳表面，双层壳外表面受冲击压力作用，单层壳体表面同样受到冲击波载荷作用；在t=2.9 ms时，爆炸载荷在双层壳外圆柱壳结构中传播同时，透射压力波通过舷间水作用在内圆柱壳表面；在t=4.5 ms时，冲击波载荷已经越过圆柱壳最高点，并且冲击波在继续向圆柱壳后方绕射传播。

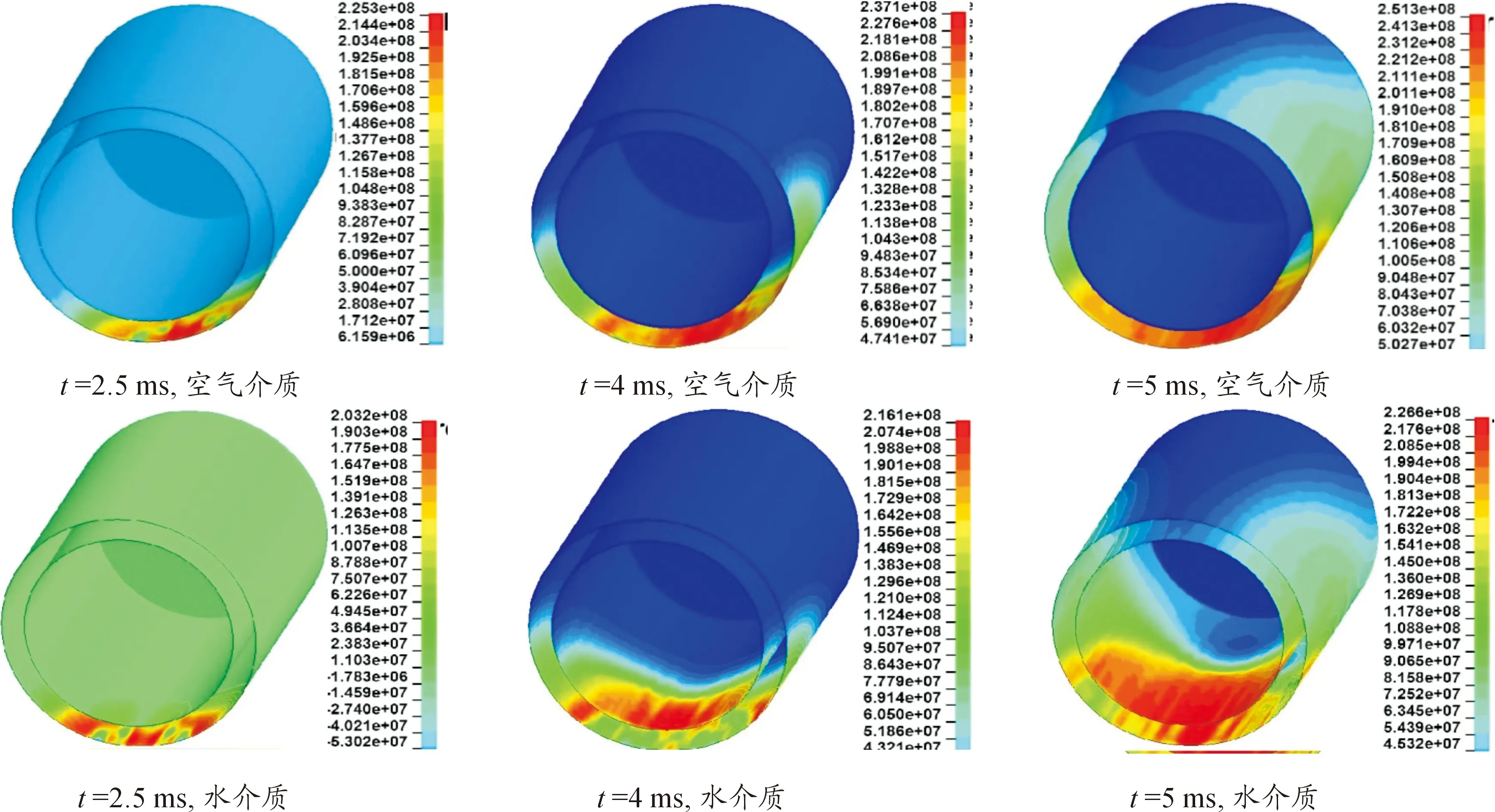
图15 双层圆柱壳结构上的压力云图

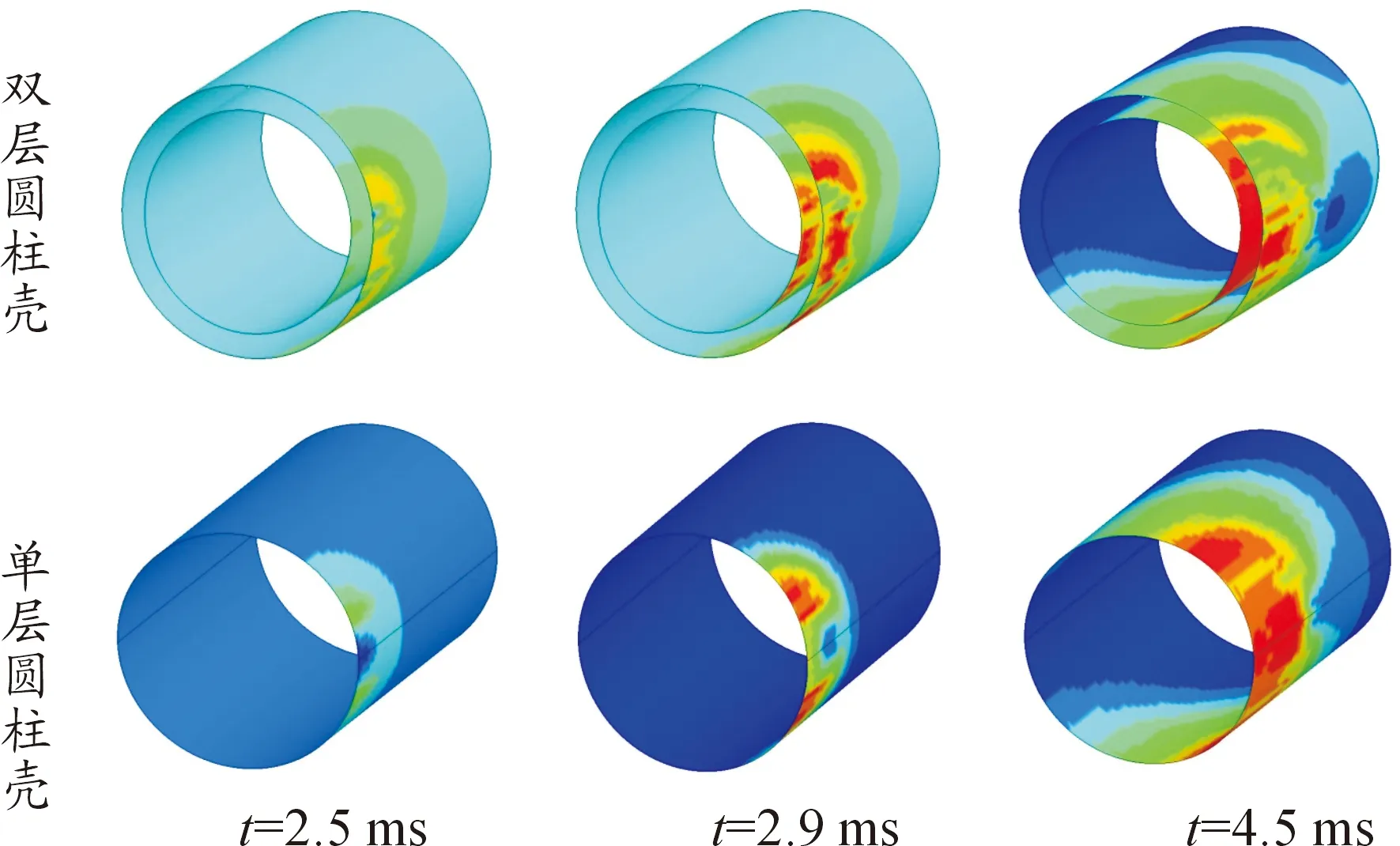
图16 双层圆柱壳结构与单层圆柱壳结构在相同载荷作用下的壳体表面压力分布图

由于计算时选用增量步为自动控制，因此在时间上没有绝对相同的时间点。图中0.21 ms时，冲击波到达双层壳结构的外圆柱壳，并且产生反射波与稀疏波，在0.23 ms时，由于舷间水的存在，透射波直接传播至内层圆柱壳结构。当冲击波压力到达内层圆柱壳结构后，由于空气阻抗作用太弱不再向内继续传播。提取测点的压力时间曲线，如图17所示。

双层壳结构位置设置中，内圆柱壳药包距离为0.5 m。外圆柱壳距离药包0.4 m。图中数据可以看出，双层壳结构的迎爆面入射压力与透射压力相差3.2倍，透射系数0.36。

环境水压的变化换转化成圆柱壳结构中的应力变化，图18为圆柱壳结构的在不同水深状态下的应力分布云图。

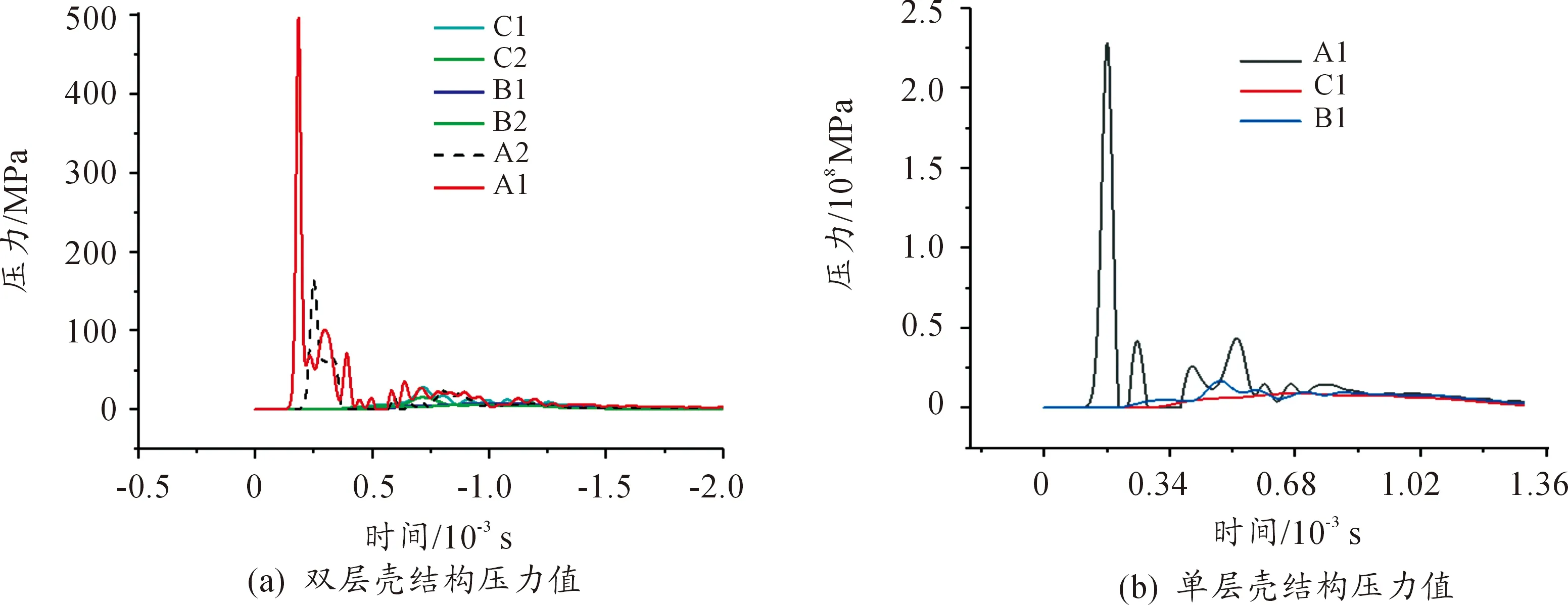
图17 壳结构压力值

图18 应力云图

4 结论

1)利用ALE算法进行水下冲击波作用下双层壳结构响应特点的仿真模拟，仿真结果与理论计算结果吻合良好，计算结构偏差较小；

2)仿真结果表明了壳体周围的冲击波传播特征，背水板与背空板透射系数存在极大差异。空气介质双层壳结构反射波高压区域明显要比水介质双层圆柱壳结构反射波高压区域大，且空气介质圆柱壳背爆面的绕射压力区域范围与压力值均大于水介质双层圆柱壳。两种不同介质的圆柱壳反射率存在明显差异，冲击波在水介质双层壳结构间不停地来回反射形成震荡。空气介质则不存在此类现象。

3)冲击波载荷压力波动规律在不同水深基本无差异性。四个水深下的压力曲线表明，水压差别是曲线差异性的主要原因。

4)研究结果对指导航行器结构设计及水下兵器设计具有一定的工程意义，也可在本试验的基础上继续研究不同体积的壳间水介质对冲击响应的影响。