优化“农夫式”课堂教学 培养学生创新能力
刘宗安 柯炳春

摘 要:结合初中数学“农夫式”课堂教学实践,从观察归纳型、开放型、阅读理解型、方案设计型、探究型等五种解题类型的设计,阐述如何优化“农夫式”课堂教学, 培养学生创新能力.
关键词:“农夫式”课堂教学;教学实践;创新能力
引言
创新能力是社会发展的需要,是新时期社会对人才的要求.培养学生的创新精神和实践能力是新时期义务教育课程改革的重点,也是初中数学教育的重点,更是培养人才的需要.初中数学“农夫式”课堂教学是一种建立在激发学生学习兴趣的基础上,让学生会学、爱学、乐学的数学课堂教学模式.本文结合近几年来的教学实践,就如何优化“农夫式”课堂教学,培养学生创新能力,谈点粗浅的看法.
1 “农夫式”课堂教学中设计“观察归纳型”问题,培养学生的创新能力
【例题1】观察下列算式: 21=2,22=4,23=8,24=16,25=32,26=48,27=128,28=256,…,则2+22+23+24+25…+22018的未位数字是__________________.
【简析】通过观察发现:2n的未位数字是四个一循环,分别为2,4,8,6.因为2018÷4=504…2,所以22018的未位数字与22的未位数字一样,都是4,从而得出本题答案.本题考查的是尾数特征,根据题意找出数字循环的规律是解答此题的关键.
【答案】6.
【点评】观察归纳型问题要求学生用归纳方法从实例中发现其存在的规律,把潜藏在表面现象中的本质挖掘出来,当规律被找出后就达到了创新的目的,这符合学生的认识规律,也为创新能力的培养提供了前提条件.
2 “农夫式”课堂教学中设计“开放型”问题,培养学生的创新能力
【例题2】如图1,在四边形ABCD中,∠ACB=∠ACD,要使△ABC ≌△ADC,则应添加的条件是 .(添加一个条件即可) .
【简析】本题已知一边(公共边)和一角对应相等,要使△ABC ≌△ADC,有三种思路可供选择:(1)若依据SAS,则应填BC=DC;(2)若依据ASA,则应填∠BAC=∠DAC。(3)若依据AAS,则应填∠B=∠D.本题主要考查学生对全等三角形判定定理掌握的熟练程度,此类添加条件题是开放型问题,答案并不唯一,只要符合全等三角形的判定定理即可.
【答案】BC=DC或∠BAC=∠DAC或∠B=∠D.
【点评】开放性问题常提供一些在问题的条件、结论、解题策略或应用等方面具有一定的开放程度的问题,解题时要灵活运用所学基础知识,多层次多角度地分析、思考问题.开放性问题可以使学生从不同角度去探索,留给学生更多的空间去发挥创造,从而培养学生的创新能力.这类问题有三种类型:(1)条件开放型(条件在不断变化);(2)结论开放型(结论有多个或结论无固定);(3)策略开放型(思维的方法和思维的途径有多种).
3 “农夫式”课堂教学中设计“阅读理解”问题,培养学生的创新能力
【点评】阅读理解题主要考查学生的阅读能力和对所学知识的整理、归纳能力.阅读理解题多以新运算、新概念、新方法的形式呈现.阅读理解题常见的类型有:(1)阅读新知识,解决新问题;(2)阅读解题过程,模仿解题策略;(3)概括归纳型;(4)阅读纠正错误,提高辨别能力[ 1 ].解决这类问题的关键要把握两点:一是掌握问题原型的特点及解决问题的思想方法;二是根据问题情境的变化,把握其规律,领会问题的本质内容,合理进行思想方法的迁移.[ 2 ]
4 “农夫式”课堂教学中设计“方案设计型”问题,培养学生的创新能力
【例题4】某工厂计划生产甲、乙两种机器共10台,其生产成本和利润如表1:
(1)若工厂计划获利14万元,问甲、乙两种机器应分别生产多少台?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?并说明哪种方案获利最大?最大利润是多少?
【简析】(1)根据“工厂计划生产甲、乙两种机器共10台和工厂计划获利14万元”,建立方程组求解即可得出结论;(2)根据“工厂投入资金不多于44万元,且获利多于14万元”,建立不等式组即可得出结论.本题主要考查了二元一次方程组、一元一次不等式组的应用,正确找出相等关系和不等关系是解本题的关键.
【答案】(1)甲、乙两种机器应分别生产6台和4台;(2)方案一:甲种机器生产3台,乙种机器生产7台,获利17万元;方案二:甲种机器生产4台,乙种机器生产6台,获利16万元;方案三:甲种机器生产5台,乙种机器生产5台,获利15万元.所以方案一获利最大,最大利润为17万元.
【点评】方案设计型问题是通过实例,提出解决问题的要求,让学生寻求恰当的解决方案.这类题型一方面考查了学生的探究意识和创新精神,另一方面考查了学生的实践能力.方案设计型题涉及生产生活的方方面面,如购物、生产配料、汽车调配、图形拼接等,所用到的数学知识有方程、不等式、函数等,即能够针对不同的实际问题,通过建立数学模型,把实际问题转化为数学问题,选择最优方案[ 2 ].解答此类题要注重综合运用转化、数形结合、方程函数及分类讨论等数学思想.
5 “农夫式”课堂教学中设计“探究型”问题,培养学生的创新能力
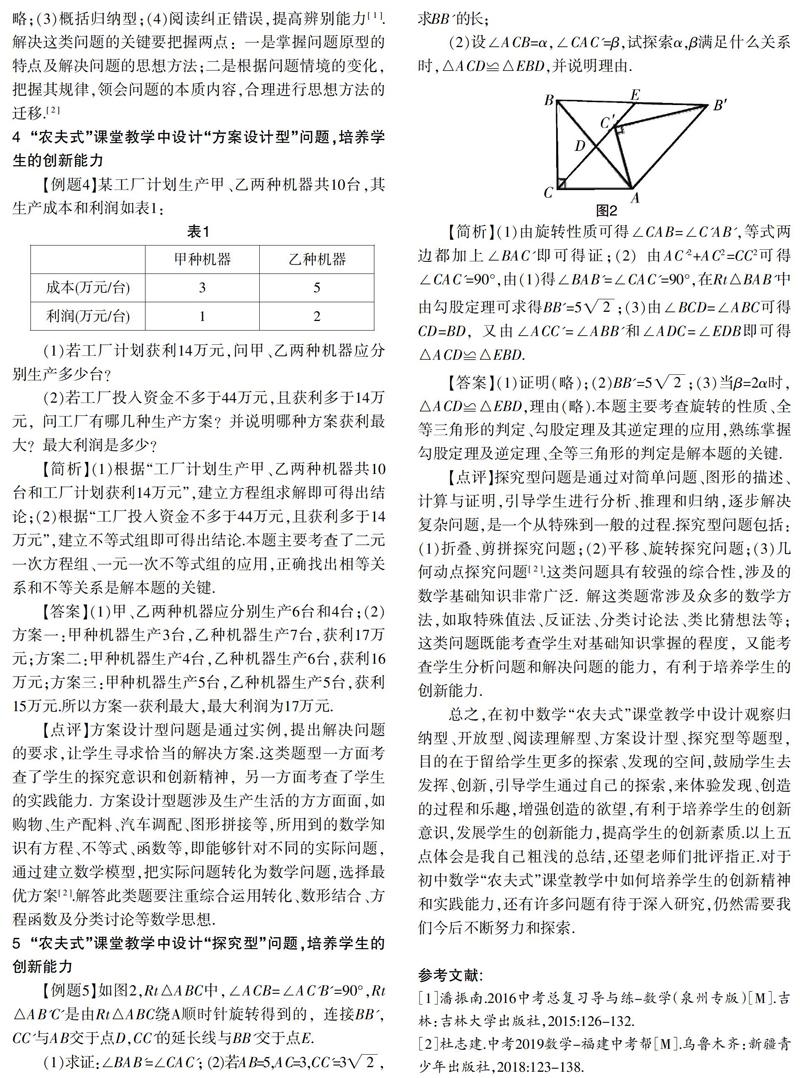
【例题5】如图2,Rt△ABC中,∠ACB=∠AC'B'=90°,Rt△AB'C'是由Rt△ABC绕A顺时针旋转得到的,连接BB',CC'与AB交于点D,CC'的延长线与BB'交于点E.
(2)设∠ACB=α,∠CAC'=β,试探索α,β满足什么关系时,△ACD≌△EBD,并说明理由.
【点评】探究型问题是通过对简单问题、图形的描述、计算与证明,引导学生进行分析、推理和归纳,逐步解决复杂问题,是一个从特殊到一般的过程.探究型问题包括:(1)折叠、剪拼探究问题;(2)平移、旋转探究问题;(3)几何动点探究问题[ 2 ].这类问题具有较强的综合性,涉及的数学基础知识非常广泛.解这类题常涉及众多的数学方法,如取特殊值法、反证法、分类讨论法、类比猜想法等;这类问题既能考查学生对基础知识掌握的程度,又能考查学生分析问题和解决问题的能力,有利于培养学生的创新能力.
总之,在初中数学“农夫式”课堂教学中设计观察归纳型、开放型、阅读理解型、方案设计型、探究型等题型,目的在于留给学生更多的探索、发现的空间,鼓励学生去发挥、创新,引导学生通过自己的探索,来体验发现、创造的过程和乐趣,增强创造的欲望,有利于培养学生的创新意识,发展学生的创新能力,提高学生的创新素质.以上五点体会是我自己粗浅的总结,还望老师们批评指正.对于初中数学“农夫式”课堂教学中如何培养学生的創新精神和实践能力,还有许多问题有待于深入研究,仍然需要我们今后不断努力和探索.
参考文献:
[1]潘振南.2016中考总复习导与练-数学(泉州专版)[M].吉林:吉林大学出版社,2015:126-132.
[2]杜志建.中考2019数学-福建中考帮[M].乌鲁木齐:新疆青少年出版社,2018:123-138.

