肯尼亚日均降雨量推求

王金星，谭鹏，李广明，张旭春

（1.中国路桥工程有限责任公司，北京100011；2.中交第二公路工程有限公司，西安710065）

1 引言

肯尼亚位于非洲东部，为热带草原气候，降水季节差异大。自20 世纪中叶以来，肯尼亚极端降雨气候年份明显增多，由强降雨引发的气象灾难风险有所增加[1]。

目前，在现行规范中还未有计算不同重现期下降雨强度的公式。可见，如何根据现存自记录的雨量资料对肯尼亚地区进行不同重现期降雨强度的计算分析，对肯尼亚地区更好的发展及规范中降雨强度公式的完善具有重要意义。

2 不同重现期日均降雨量的推求

2.1 概述

目前，设计城市中雨水、排水管道及小汇水流域排水渠道时，短历时暴雨强度公式是设计者的主要依据。我国已对暴雨强度公式的编制与应用管理做了规定，但是，由于实际工程的复杂性与多变性，往往会出现违背规范的现象，给市政工程建设乃至城市建设的推进留下极大的安全隐患。随着社会发展的推进，法规的健全，科学技术的进步以及相关研究的深入，市政工程的规划及设计水平求能够满足更高、更科学、更具说服力的要求。暴雨强度公式需要做到普及，那么对公式的精度要求也达到了更高的水准。所以，需要对公式编制涉及的一系列问题研究得更加透彻，以便于减少暴雨强度公式编制的误差，提出更好的公式编制方法。

目前，我国的暴雨强度计算公式为：

式中，A1、C、b、n均为地方性参数；T为重现期；t为暴雨历时，mi n；i为暴雨强度，mm/min。暴雨历时一般采用5min、10min、15min、20min、30min、45min、60min、90min、120min 共9 个 历时。重现期一般取0.25a、0.33a、0.5a、1a、2a、3a、5a、10a、20a、50a、100a。可见，推求暴雨强度时，需要充足的降雨量数据，但现实中降雨量数据并不满足要求，故研究降雨量的分布模式推求降雨量十分重要。

目前，暴雨强度公式的编制需要根据当地自记雨量资料，再结合数理统计的方法判断并确定暴雨强度抽样的分布模式，从而计算出各历时不同重现期的理论暴雨强度值。其中，还需要设计者采用适当的方法得到公式中的某些参数。目前，国内外通常采用指数分布及皮尔逊（Pearson）Ⅲ型分布模式对暴雨强度抽样频数分布进行拟合，并采用经验值与计算相结合或图解与计算相结合的方法进行参数的确定，但是确定参数的方法已经逐步被数值求解法取代。另外，需要指出的是，由于肯尼亚历史国情的影响，在推求上述暴雨强度公式时，现存的数据并无法满足要求，其中逐小时及更短时间间隔的降雨量数据获得的难度更大。

2.2 暴雨强度抽样概率分布及拟合

2.2.1 指数分布

在指数分布模式下，其概率密度函数和分布函数分别为：

式中，xi（i=1，2，…，N）为样本的降雨量；a为分布曲线离散程度的参数；r为分布曲线的下限。

分布函数超过概率：

故对应于重现期T的分位数：

记1/a=α，接着，根据抽样的经验概率分布及最小二乘法，计算确定系数α、r，再利用式（5）计算各重现期的分位数。

2.2.2 皮尔逊（Pearson）Ⅲ型分布

在皮尔逊Ⅲ型分布模式下，其密度函数和分布函数为：

式中，参数α≥0，β≥0，抽样变量xi≥0，分别为概率曲线的尺度和形状；a为概率曲线的起点与序列零点之间的距离，Γ（α）为关于α 的函数。当考虑采用皮尔逊型Ⅲ分布来拟合暴雨强度的抽样资料时，首先要确定参数α、β、a。下文中，将采用矩法和极大似然法进行参数的确定。

根据矩法，得到其数学期望、方差和偏度系数分别为：

由此得到：

接着，考虑采用权函数进行参数的修正减小文中使用矩法进行皮尔逊Ⅲ型参数的估计误差，即：

式中，x¯为样本的均值为样本的均方差；Cs为偏度系数；E为加权后的一阶矩；G为加权后的二阶矩。而

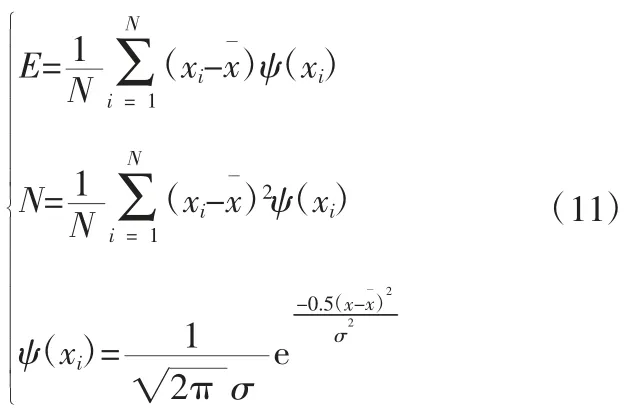
式中，ψ（xi）为正态概率分布的密度函数；N为样本（降雨量）数量。将估计的参数进行加权之后，就减少了采用矩法造成的误差，计算精度自然随之提升，这就是“权函数法”。

根据极大似然法函数，可以得到：

先将式（12）消去 β，再根据已知 ψ（α）=-0.577216+（a-1）为正整数，故采用迭代法分别求解参数α、β。

在皮尔逊Ⅲ型概率分布模式中的参数确定后，通过采用满足一定精度要求的拟合曲线可以进行各概率或重现期所对应的分位数的估算。其中的参数α 或偏度系数Cs能够控制该分布曲线在某概率或重现期所对应的分位数。因此，在实际工程中，当某个参数α 或Cs已知时，可通过曲线离均系数表计算概率P或重现期T对应的分位数。而“适线法”就是对Cs作适当修正，使得其拟合误差达到最小。

2.2.3 韦伯（Weibull）分布

在三参数韦伯分布模式下，其概率密度函数和分布函数为：

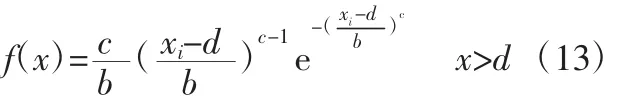
式中，b 为尺度参数；c 为形状参数；d 为位置参数。特别的，当d=0，c=1 时，即为指数分布。当 d=0 时，为二参数 Weibull 分布。因此，指数分布可看作韦伯分布的特殊情况。下文中选用矩法确定参数 b、c、d。

根据其前三阶矩，采用积分可以求得：

故重现期所对应的分位数为：

3 Jomo Kenyat t a Nairobi 实例

由于数据所限，本文利用前述的概率分布模式对肯尼亚首都内罗毕（Nairobi）市（资料年限：1957—2018 年）Jomo Kenyatta Nairobi 台站（纬度：1.31°S，经度：36.91°E，海拔高程：1624m）的逐日历史降雨强度数据进行拟合。数据通过人工逐个查询的方式在https://en.tutiempo.net/数据库内抓取。

图1 表示1980—2018 年肯尼亚的日均降雨量，在2010年2 月13 日，出现了最大日降雨量341.54mm，该数据为近40年来最大降雨，在1980 年也出现了大于300mm 的日均降雨量。不考虑旱季和雨季情况下，上述38 年间，该台站的日均降雨量为7.59mm，标准方差为9.97mm。这些数据对肯尼亚的气象研究和区域内相关基础设施的建设和防灾具有重要意义。在未来的几年中，可能还会有超过300mm 的日均降水量，短时强降雨对路基的影响不可忽视。

重现期是指在一定年代的雨量记录资料统计期间内，大于或等于某个暴雨强度的降雨出现一次的平均间隔时间，为该暴雨发生频率的倒数。即某个程度的雨量，多少年出现一次，也是道路排水设计的标准。该数据也是铁路与公路等基础设施建设部门十分关心的数据。基于上述历史降雨记录，采用正态分布、对数正态分布、Weibull 分布、Chi2 分布通过编制相应的Python 计算程序推求了不同重现期下肯尼亚日均降雨量的情况（见表1）。

图1 肯尼亚（1980—2018 年）日均降雨量（Jomo Kenyatta Nairobi 台站）

表1 肯尼亚（1980—2018 年）日均降雨量推求（Jomo Kenyatta Nairobi 台站）

从计算结果来看，采用正态分布拟合的结果得到的日降雨量数据在各个重现期下均是最小，而Chi2 分布拟合误差略大；相对而言，使用三参数韦伯分布和对数正态分布拟合抽样的效果较好。而尽管正态分布的拟合结果与其相差大，但是由于正态分布在理论上可能出现降雨值为负数的情况，因此，不建议使用。因此，该地区10a 一遇的日降雨量在20～23mm 较为恰当；而20a 一遇的日降雨量则在24～30mm 较为恰当；50a一遇的日降雨量则在33～40mm 较为恰当，100a 一遇的日降雨量则在38～45mm 较为恰当。

4 结论

本文在不同重现期的降雨量的推求中对概率分布模式（指数分布、皮尔逊Ⅲ型分布、韦伯分布、对数正态分布）进行选择，再通过对多种参数估计法的对比和择优，对如何提高分布模式的拟合精度具有一定的积极意义。而通常情况下，利用对数正态分布或者Weibull 分布推求不同重现期下的降雨量，其参数拟合精度要高于其他概率分布模式。