非线性能量阱系统受基底简谐激励的参数优化分析

刘良坤， 潘兆东， 谭 平， 闫维明， 周福霖,

(1. 东莞理工学院 生态环境与建筑工程学院，广东 东莞 523808；2. 广州大学 工程抗震研究中心，广州 510405；3. 北京工业大学 建筑工程学院，北京 100124)

在一定的初始能量下，非线性能量阱(Nonlinear Energy Sink, NES)能够产生靶能量(Targeted Energy Transfer, TET)传递现象，由于这一现象具有较高的能量耗散效率，近年来得到了广大学者的重视[1-5]。当受到简谐激励时，NES系统将出现一种准周期响应机制，这种机制称为强调制反应(Strongly Modulated Response, SMR)，有关SMR的研究详见文献[6-9]。针对NES系统的SMR，Gendelman等[10]对其及系统吸引域进行了研究，得到了NES最优刚度参数的优化范围，并与TMD(Tuned Mass Damper)的减振性能作了对比[11]，但分析时忽略了主系统阻尼影响。为了获得更高的耗能效率，很多学者对NES系统的做了大量优化工作，其中Nguyen等[12]利用靶能量传递及慢不变流形(Slow Invariant Manifold, SIM)特性得到了初始能量下的最优刚度；为了获得简谐激励下NES的最优刚度，Vaurigaud等[13-14]，在Nguyen等的基础上得到了NES的最优刚度设计公式，但其假定达到阈值前系统保持线性状态，会带来一定误差，并且不能够保证截止频率范围内响应都不放大。Gourc等[15]利用SMR的特点获得NES的最优刚度区间，但求解过程需要利用分叉解，计算复杂；Viguié等[16-17]利用分叉程序直接得到最优刚度和阻尼，但未考虑系统阻尼，仍存在局限性，而且寻找分叉解中的最优值也并不容易。此外，为获得较好的吸能效果，一些研究人员又提出了新型NES系统，如孔宪仁等[18]采用两自由度NES对主系统进行控制，并用Starosvetsky等研究中的方法得到最优刚度；李海勤[19]则利用非线性阻尼的NES系统进行减振研究；楼京俊等[20]建立了带有弱线性刚度项的强非线性吸振器的动力学模，并分析了多频激励下的减振效果；王菁菁等[21]等研究了轨道NES；最终这些新型NES系统均取得了较好的吸能效果。

上述研究主要集中于NES主系统受脉冲激励或简谐激励的减振分析，然而系统也常受到基底激励，如地震激励、设备基底激励等，因此有必要对基底简谐激励下的NES系统减振特性及其最优参数进行研究。针对该类激励(本文以地面加速度激励为例)的NES系统，本文将考虑主系统阻尼，并试图利用SMR的特点及推导的吸引点方程来得获取最优刚度范围，从而减小计算量，然后通过慢变系统数值寻优，最后对该系统减振特性进行分析。

1 非线性能量阱系统模型

受基底激励时(以地面加速度激励为例，如图1所示)，带光滑立方刚度的非线性能量阱系统振动微分方程为

(1)

图1 基底激励的非线性能量阱系统模型Fig.1 Nonlinear energy sink model under base excitation

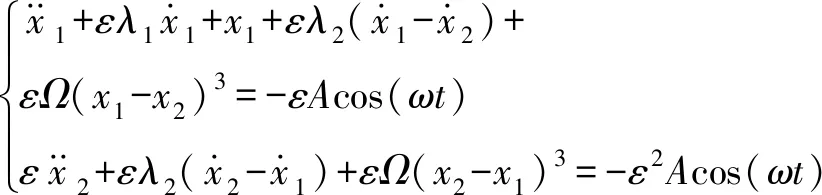
(2)

引入新变量

(3)

再次简化系统，将式(3)代入式(2)变换后得

(4)

(5)

由于本文主要研究系统在外激励下的1∶1共振，此时可假定ω=1+εσ(σ为失谐参数，表示系统实际的共振在假定频率比附近)，式(5)变为

(6)

从上述慢变方程看，与主系统受激励相比，基底激励时，NES系统的激励幅值中含有ε2项，这与振动微分方程式(1)中NES自身也受惯性力激励有关。将上式泰勒展开，并引入多尺度变换

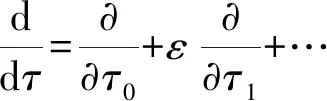
(7)

对式(6)多尺度变换后，取ε的前两阶得

(8)

(9)

(10)

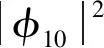
(11)

其中，式(11)的解依赖于Z1和λ2，但Z1对其解的个数无影响，对式(11)求导得

(12)

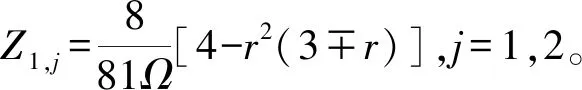
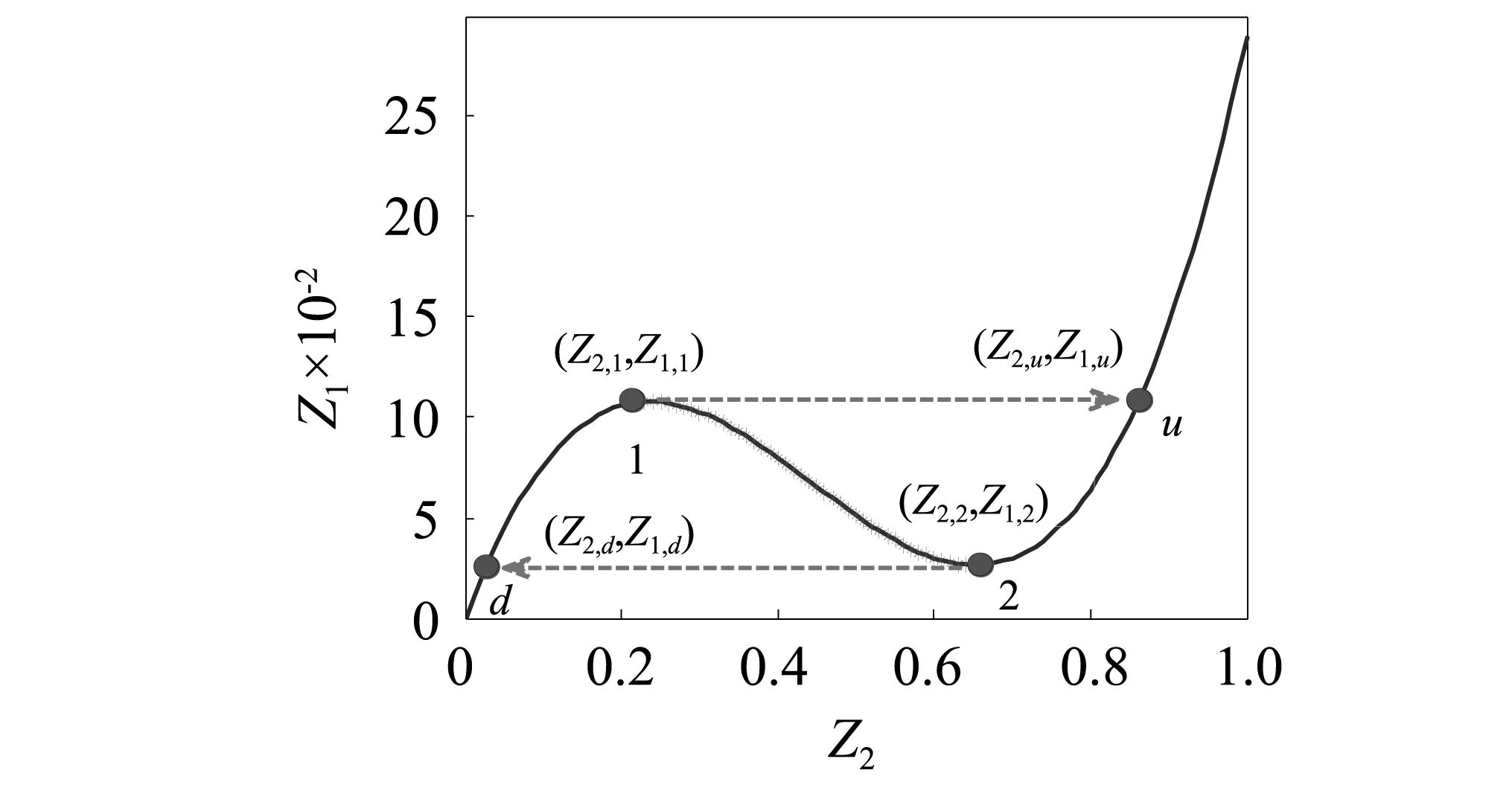
图2 慢不变流形Fig.2 Slow invariant manifold

(13)

(14)

由于，

(15)

式(14)变为

(16)

对式(16)取共轭并简单变换后得

(17)

利用极坐标形式φ20(τ1)=N2(τ1)eiθ2(τ1)表示式(17)并分离出幅值与幅角则有

(18)

其中,

显然式(18)存在两种形式的不动点(平衡点)

(19)

与

(20)

(21)

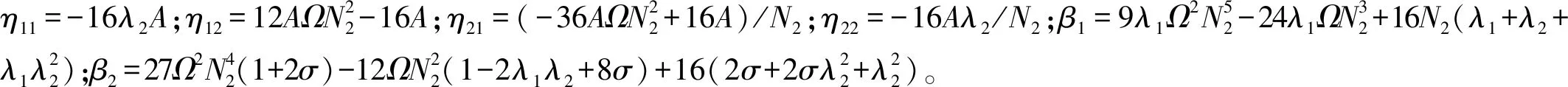
(22)

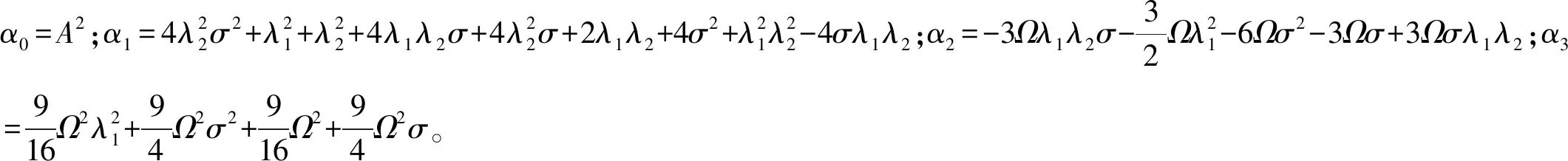
(23)

式(23)的解析形式复杂，可用数值解获得相应的吸引点。

(24)

那么只要结合式(21)任一式即可获得到折奇点解。若采用式(21)的第一式容易得到

(25)

折奇点的相应幅角为

(26)

这两对幅角对应于图2的两极值点，第1对折奇点存在时需满足以下条件

(27)

显然，只要满足第一式即可

A≥A1c=

(28)

同理可以得到第2对折奇点存在的条件为

A≥A2c=

(29)

折奇点的存在是SMR现象出现的必要条件，当SMR出现时，满足A>A1c，但A>A1c并不一定能够产生SMR，因为式(28)与式(29)并没有体现失谐参数的影响；由于失谐参数的影响，系统响应也可能吸引至普通吸引点或者产生弱调制反应。此外，从上述折奇点条件的推导过程看，系统受基底简谐激励与主系统受简谐激励的多尺度分析前两阶方程基本相同(仅幅值符号相反，实际上折奇点与符号无关)，那么两种激励形式所产生折奇点的必要条件是相同的。

2 最优刚度区间

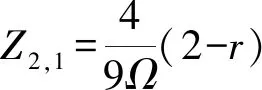
(30)

式中：a=2-r,显然刚度下限值Ωd与激励幅值A2成反比关系。当满足式(30)时，即满足SMR出现的必要条件，此时也就保证了Z1≥Z1,1。

当满足式(29)时，上折线的将产生折奇点，即Z2≥Z2,2的范围内存在普通吸引点(见图2)，但为了尽可能的保证SMR产生，吸引点的纵坐标值Z1不应超过峰值Z1,1，即

(31)

写成如下形式

(32)

(33)

求解式(33)有

(34)

此时只要将式(34)代入式(22)，就可计算出刚度上限值Ωu。值得注意的是，式(22)的σ将影响刚度值计算，但可计算多个σ，然后取其最小获得刚度上限值。尽管上述方法从数学角度看不够严谨，但可得到较小的最优刚度范围，对减少计算量十分有利。

3 数值验证与参数优化分析

获取最优刚度范围时，需要利用NES的吸引点，因此有必要对所推导的吸引点方程及其相关内容进行论证，其它有关折奇点及SMR的详细讨论见Starosvetsky等的研究，此处仅将涉及的内容作简要介绍。假定NES系统参数为的m1=1,ω1=2，λ1=0.2，λ2=0.2,Ω=4/3,ε=0.01,根据式(28)与式(29)容易计算出折奇点出现的条件为A1c=0.256 4与A2c=1.024 2。

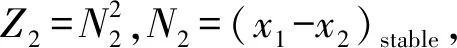
图3 吸引点论证 A=0.2,δ=0Fig.3 Fixed point verification A=0.2,δ=0

(3.750 7，0.458 0)，显然这两种结果相近，也就说明利用式(22)和式(23)计算吸引点是合理的。图3(d)中慢变方程与振动微分方程的稳态解分别为(x1-x2)stable=0.458 2，(x1-x2)stable=0.459 2可见，这两者相差不大，且与吸引点数值也十分接近，这就进一步说明利用吸引点公式计算是合理性的。

假定A=1.2,δ=2，对比吸引点的基本情况，如图4所示。由于A=1.2>A1c=0.025 64，已具备SMR出现条件，但A=1.2>A2c=1.024 2将产生上折奇点，此时上折线会产生上吸引点，如图4(a)所示；系统最终稳态响应也可能吸引到该吸引点，如果初始条件合适，还可能出现下吸引点和不稳定响应，即有多解共存的现象。利用Runge-Kutta法得到需关心的上吸引点(1.249 5，0.735 2)，如图4(a)方框；当采用式(22)和式(23)计算可得多个吸引点，其中的上吸引点为(1.249 5，0.734 9)，易知这两种计算值几乎相同。对比慢变方程与原振动方程，如图4(b)与图4(c)，显然两者围绕慢不变流形图变化规律相似；最终所得时程曲线如图4(d)，稳态幅值分别为(x1-x2)stable=1.204 0，(x1-x2)stable=1.275 0,可见，尽管有微小误差，但两者计算结果仍保持一致，且与吸引点的数值也接近，这再次证实了本文所推导的吸引点方程是合理的。

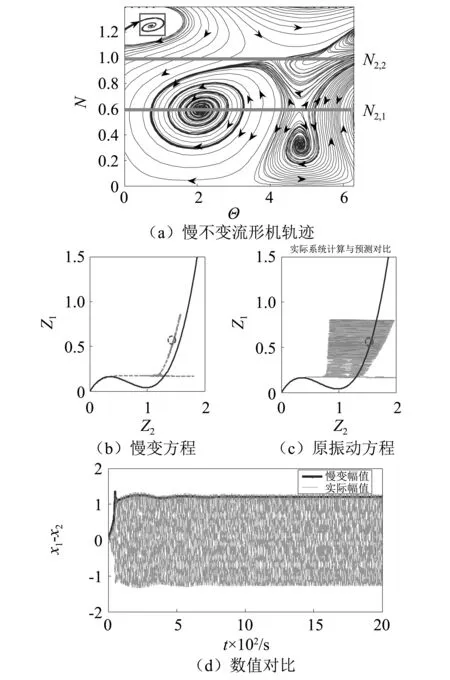
图4 吸引点论证 A=1.2,δ=-2Fig.4 Fixed point verification A=1.2,δ=-2

吸引点的合理性得到确认后，此时可根据吸引点求解最优刚度范围，考虑到NES系统存在非线性，难以得到最优参数解析解，Gourc等的分析也并未得到较好的结果，仅提供了最优刚度范围，但计算繁琐且需要利用分叉解。若采用本文方法则较容易获得最优刚度范围，结合慢变方程式(6)，最终搜寻最优刚度的工作量将减少很多。取NES系统参数为m1=1,ω1=2,A=1，λ1=1，ε=0.02,假定有三种NES阻尼参数分别为λ2=0.1,0.2,0.3，利用式(30)求解刚度下限值，然后用式(22)变化δ得到最小刚度上限值，最后得到的刚度范围：[0.302,0.709],[0.446,1.455],[0.643,2.247]，对应失谐参数δ分别为-1.301，-1.654，-1.912，可见最小刚度刚度上限值出现在0失谐参数左侧。

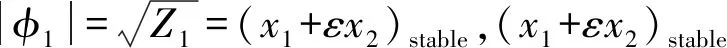
图5 优化分析Fig.5 Analysis for optimization

利用λ2=0.2的最优刚度参数，绘出NES系统与TMD系统的频率比、激励幅值与主系统能量关系如图6所示，其中网格为未安装任何装置的系统能量。分析图6可发现NES系统在A>1的区域内，部分频带的能量有放大现象，而在A<1有却不同程度的减小，需要注意的是NES的最优刚度参数是在A=1条件下得到的，这表明NES易受激励幅值影响；然而TMD系统在任何激励幅值下均有能量放大的区域，但在频率比为1附近并无放大现象且耗能效率较高。关于这两种系统在其他方面的优缺点对比也可见文献[23]。

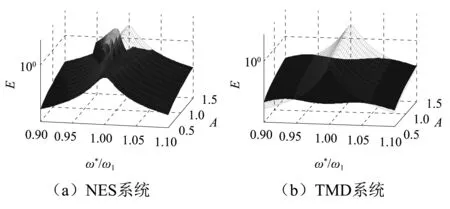
图6 频率比、激励幅值与能量关系(λ2=0.2,Ω=1.25)Fig.6 Relationship of frequency ratio, excitation amplitude and energy(λ2=0.2,Ω=1.25)

图7 NES刚度、阻尼参数与能量关系Fig.7 The relationship of stiffness, damping parameters and energy

4 结 论

本文采用复变量平均法推导了基底简谐激励作用下的1∶1共振下的慢变系统方程，并利用多尺度法推得了强调制反应的必要条件以及吸引点解析方程；然后结合SMR的特点及吸引点解析方程获得了最优刚度下限值与上限值。结果表明：

(1)吸引点方程计算结果与Runge-Kutta计算的吸引点数值相同，且与原振动方程计算的稳态响应值一致；与直接积分计算NES系统，利用慢变系统方程，只需一阶积分，具有更高的效率，且结果相对精确。

(2)所得到的最优刚度区间范围合理，缩小了最优刚度的取值范围，方便得到系统的最优刚度。

(3)与TMD减振效果相比，NES具有较宽减振频带，但在主频附近减振效率更低且受激励幅值影响。NES阻尼参数的对主系统能量的敏感性较低，不过随阻尼参数的增大，最优刚度区域更宽。