物理奥赛抛体问题的处理与运用

殷仁勇

(江苏省仪征中学，江苏 扬州 211900)

在物理奥赛辅导教学过程中,会涉及到抛体运动问题,如果用初等数学处理,要用到比较复杂的三角函数知识,且运算量大,有时思路比较巧妙,学生难以想到.本文另辟蹊径,使用了高等数学复合函数求导,解一阶常系数非齐次微分方程等数学工具,思路直接而又简单.以下就抛体运动的各种情形分别举例讨论．

1 使用斜抛运动轨道方程讨论各种极值问题

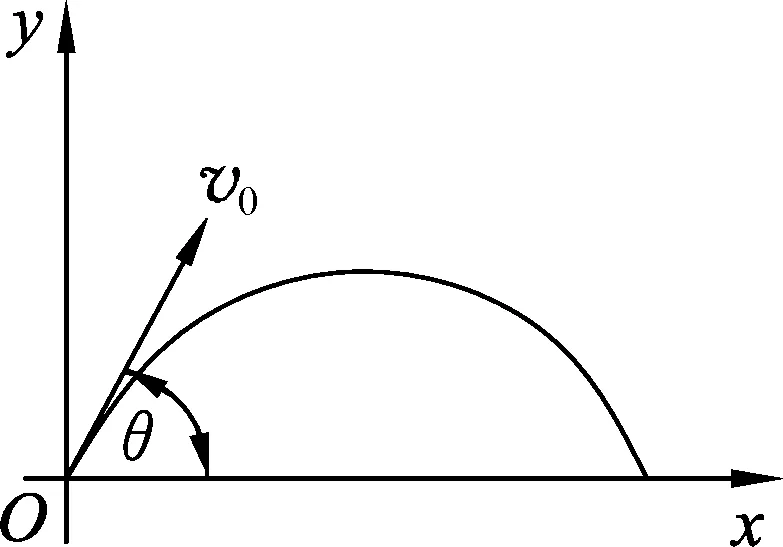
图1

(1)x,y一定,θ(tanθ)满足什么条件,v0(v02)取极值?

例1.足球运动员在距球门正前方s=11 m处的罚球点,准确地从球门正中横梁边沿下踢进一球,横梁边沿离地高度h=2.5 m,足球质量为m=0.5kg,空气阻力不计,求运动员至少要对足球做多少功?

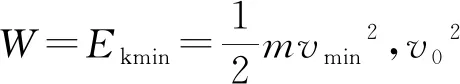
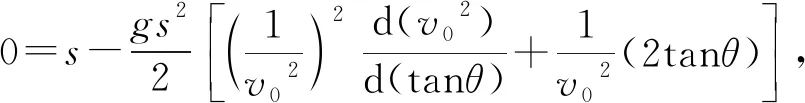
(2)y,v0(v02)一定,θ(tanθ)满足什么条件,x取极值?

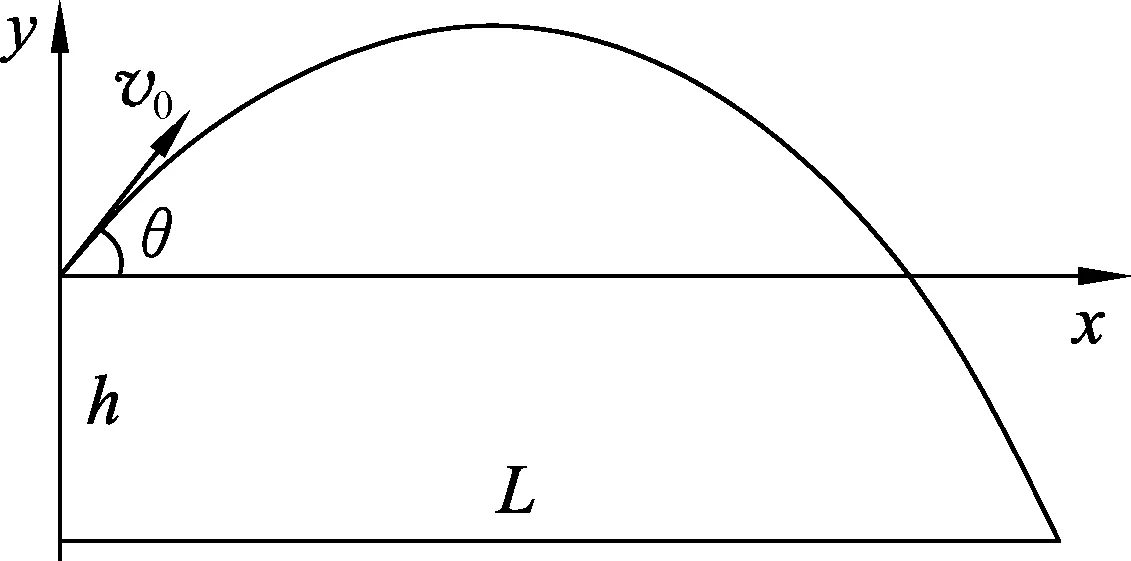
图2

例2.如图2所示,抛射体的初速度v0已知,抛出点距离地面的高度为h,求抛射体的水平射程L的极值．

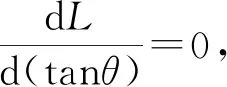
(3)x,v0(v02)一定,θ(tanθ)满足什么条件,y取极值?

例3.一人在离墙x处踢一足球,若足球初速v0为定值,求击中墙上可能的最大高度y．

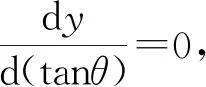
2 平抛运动考虑kv空气阻力

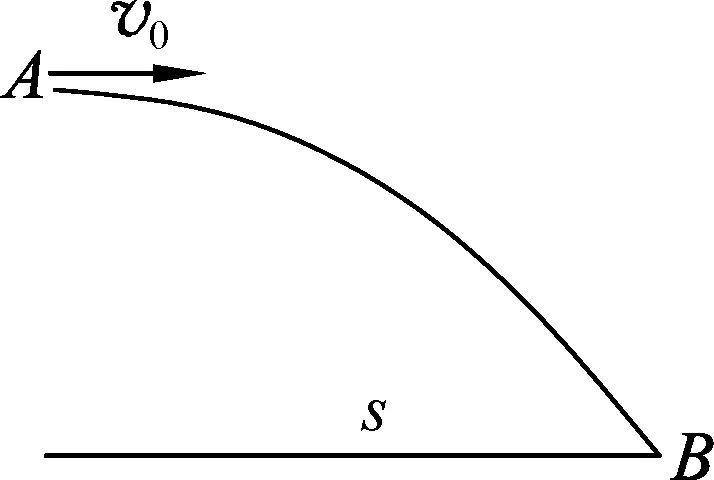
图3

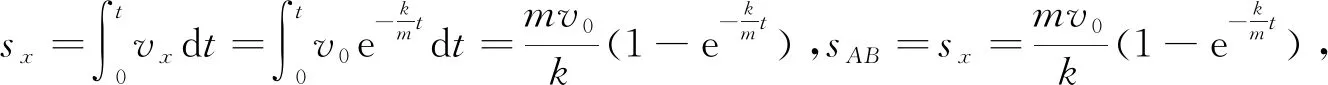
3 斜抛运动考虑kv空气阻力

例5.质量为m的抛射体初速为v0,抛射角为θ,在空气中运动时,所受阻力与速率成正比,比例系数为k,试求轨迹方程,并验证当k→0时变为斜抛运动的轨道方程．[3]

由以上两式消去时间t,得出抛射体的轨迹方程为