多角度处理一道电聚焦问题
涂德新
(江西师范大学附属中学,江西 南昌 330046)
1 问题引入[1]
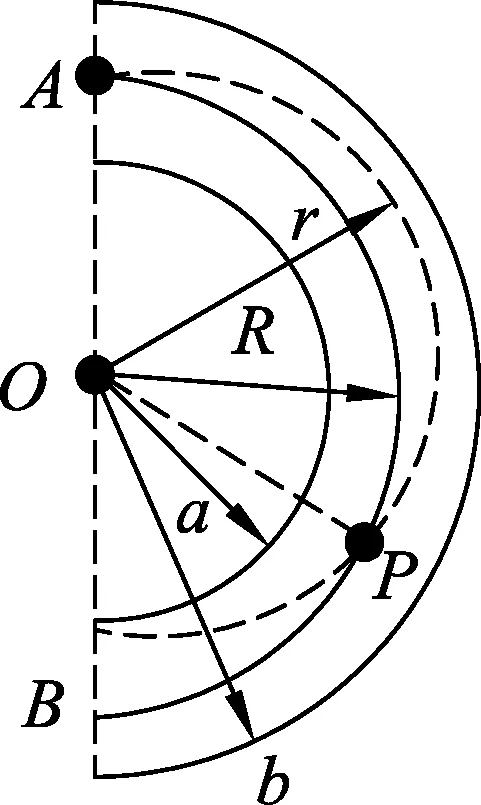
图1
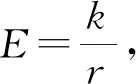
2 稳定时的速度
设初速度与入射处直径垂直的带电粒子刚好匀速圆周运动时的线速度为v0,由电场力充当向心力
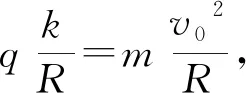
3 动力学法求周期
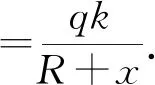

(1)
选择以O点为极点且随电荷运动的转动参考系来分析,电荷受到离心惯性力的作用
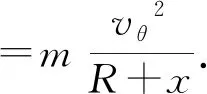
电荷在运动的过程中角动量守恒
mv0Rcosβ=mvθ(R+x).
消去vθ可得
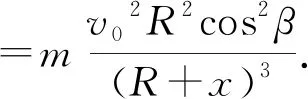
注意到β≪1(cosβ≈1) 以及x≪R上式可以改写为
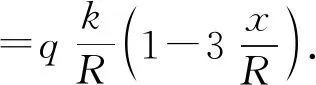
(2)
于是电荷在转动参考系中径向受到的合力为
F=F惯-F电.
(3)
4 微分方程法求周期
对电荷径向运动写出牛顿第二定律
(4)
电荷角动量守恒
(5)
电场力
(6)
由(4)-(6)式可得

由于x≪R,上式可以改写为
注意到L=mv0Rcosβ在β≪1 时L=mv0R.于是上式可以改写为
(7)
5 能量法求周期
电荷在运动的过程中能量(动能和电势能的总和)守恒,与出发时的能量相等.
(8)
电荷在运动的过程中角动量守恒
L=mvθ(R+x).
(9)
由(8)(9)式可得
由于x≪R,可以将上式改写为
β≪1则角动量L=mv0Rcosβ=mv0R,于是上式可以改写为
这是简谐运动的能量方程,故周期
6 有效势能法求周期

可以把离心势能和电势能之和叫有效势能V′=Vc+V.代入有
(10)
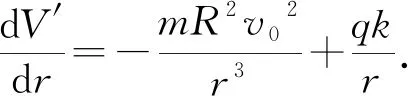
再求r=R处时有效势能的二阶导数
可见电荷在r=R处时是稳定平衡状态.
将有效势能在r=R附近按泰勒级数展开
将(10)式代入可以求得
于是在r=R附近的运动是简谐运动,其周期
7 求电聚焦位置
电荷沿角向几乎是匀速圆周运动,当电荷再次回到圆周轨道上时,时间为半个简谐运动的周期,可求聚焦的位置角度
8 后记
文中用4种方法处理了这个电聚焦问题:方法1是在转动参考系中研究电荷在径向的受力,发现径向恢复力与位移成正比且方向相反,这是简谐运动的动力学判据;方法2用数学的方法研究了电荷在径向运动的微分方程.发现电荷在径向的运动正好是简谐运动;方法3用能量的方法处理了电荷的径向运动,结果用能量判据表明电荷径向是简谐运动;方法4用有效势能的方法发现电荷在圆周的轨道上是稳定平衡,并且求出了径向振动的周期.发现粒子束可以准确聚焦,从而实现了这个问题的多角度处理.

