随风潜入夜 润物细无声

贺红叶

一、思考缘起

《义务教育数学课程标准（修订版）》中课程总体目标第一条是：“通过义务教育阶段的数学学习，学生能够获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验.”从“双基”变化到“四基”，增加了基本思想、基本活动经验.其中的基本思想就是指数学思想方法.数学思想方法博大精深，它蕴涵于数学材料之中，有着丰富的内容.而教材新增的“数学广角”这块内容正是有效渗透数学思想方法很好的载体.

二、教材解读

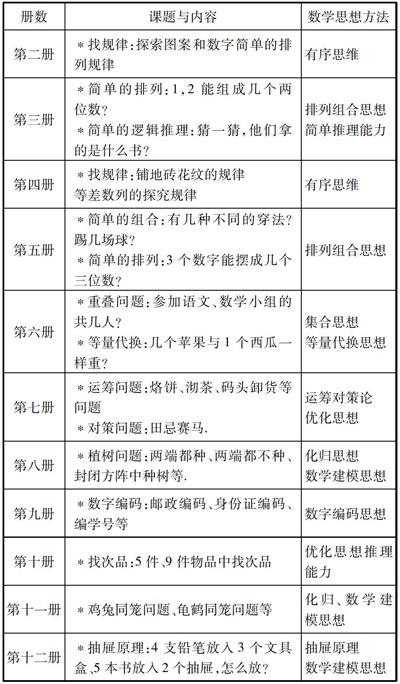
根据学生的心理发展规律及所学内容的特点，一些重要的数学思想是采用逐步渗透、深化、螺旋上升的方式进行编排.以下是十一册教材数学广角的内容编排梳理：

通过对整套教材中数学广角知识的细致梳理，能够让我们更深入地去准确把握体系中各个知识点之间的联系，同时也发现教材编排的特点是从注重形象具体思维逐步过渡到注重抽象思维，很多數学思想方法的渗透是由浅入深、螺旋上升、逐步深入的.

三、误区分析

如何把握好“数学广角”内容的教学目标、教学方法是部分数学教师一直困惑的和急需解决的问题.主要存在以下几个误区：对教学目标认识上的偏颇导致教学活动缺乏数学思想方法的体现，把数学课上成实验操作课，没有对数学思想方法进行提炼;目标定位过低，忽视或简化教学过程，让学生没有经过深入的思考、探索就获得结论;目标定位过高，一味追求教学的深度，导致教与学的畏难情绪.

四、引发思考

（一）广度与深度如何把握

教材设置数学广角内容的本意：从教学目标的把握来看，它首先应定位于通过数学活动，使学生感悟数学思想方法，建立数学模型，学会灵活运用数学思想方法尝试解决实际问题，体验解决问题的多种策略、方法.所以，教师在教学中一定要适当整合教学内容，细化教学环节，有意识地创设多种实践活动，引导全体学生去观察、实验、操作、探究，通过数学活动产生对数学思想方法的感悟和内化.

比如，在三上教材中安排继续学习排列与组合的内容，与二上教材内容相比，这册教材的内容更加系统和全面，教师如何把握好教学要求呢？鉴于这块内容的活动性和操作性比较强，可以采取观察、猜测、动手实践及小组合作学习的方式让学生经历找出事物的排列数和组合数的过程.在教学中只要求学生能根据实际问题采用罗列、连线等方式，找出简单事物的排列数和组合数，并能感受到有的与顺序有关，有的与顺序无关，初步体会到排列与组合的不同.教师在教学语言的运用中应尽量避免出现排列、组合这些术语，也无须跟学生解释.本课重在活动过程中向学生渗透排列与组合的数学思想，并初步培养学生有顺序地、全面地思考问题的意识.

由于数学广角中设置的课程内容所体现的思维含量比较高，而学生的认知起点不同、思维能力不同，因此，教师应根据学生的实际情况来制订有差异的知识技能目标，尽量保证人人参与，做到既面向全体又关注差异，真正做到“下要保底，上不封顶”.

（二）体验与结论孰主孰次

一般而言，数学思想方法比数学知识更抽象，学生不可能照搬照抄.因此，在我们的教学活动过程中，学生的亲身参与、体验相当重要，没有参与就不可能对数学知识、数学思想方法产生深刻的体验;没有了体验，那数学思想方法的领悟只能是一句空话、套话.不少教师由于自身数学素养的缺失，在教学“数学广角”内容时，很容易顾此失彼，或重视了对教学情境和操作活动的创设，忽视了对教材中所隐含的数学思想方法的挖掘;或关注了规律、思想方法的总结，而忽略了在课堂教学中留出更多的时间、空间给学生进行感悟内化.

例如，有位教师在教学五年级下册“找次品”一课时，虽然创设学生操作活动的环节，但却流于形式，随后就直接告诉学生：首先将要找的产品分成3堆，而且要尽可能地平均分.这种因为活动过程要占用大量时间，教师就“删繁就简”的做法，让学生的体验如蜻蜓点水般浅尝辄止，只知其然，不知其所以然.这样的教学无法真正达成“面对实际问题时，能主动尝试着从数学的角度运用所学知识和方法寻找解决问题的策略”的目标.显然，这种重视结论、忽视体验的做法对学生的思维发展是极为不利的.

由此可见，教师一定要在教学中关注体验过程，注重渗透思想方法，落实数学思考，才能使学生的思维得到长足的锻炼.同时，教师要不断提升自身的数学素养，只有在教学中长期让学生去亲身体验，才能不断累积经验，从而实现“面对实际问题时，能主动尝试着从数学的角度运用所学知识和方法寻找解决问题的策略”的目标.

（三）思想与规律孰轻孰重

《数学课程标准》指出：知识与技能、数学思考、解决问题、情感与态度是义务教育阶段数学课程的总目标，这四个方面的目标是一个密切联系的、不可分割的有机整体.显然，这四个目标落实到数学广角内容中，数学思考的含量更多些.因此，教师要充分地理解教材、挖掘教材中所蕴含的数学思想方法，在教学时注重让学生通过观察、实验、操作、分析、感悟数学思想方法的魅力.

四下“植树问题”教学片段：教师通过引导学生把复杂问题简单化，把原本100米的路程想象成20米来种植，接着利用画图引导学生发现一个间隔对应一棵树，从而发现如果两端都栽这类情况“棵数=间隔数+1”这样的规律之后，在课的结尾匠心独具地设计了下面的练习：圆形溜冰场一周全长150米，如果每隔15米安装一盏灯，一共需要多少盏？大部分学生根据前面的所学规律进行迁移，脱口而出“11盏”.这时教师引导全班动手简单地画个圈，找一找在圆上间隔数和灯数之间有什么关系？找到规律了吗？只用150÷15=10（盏）就解决了问题.这样的过程不但让学生经历了知识建构的“破”与“立”，同时为后续的“只种一端”问题的研究打下了基础.此时，教师引导学生明白其实规律本身并不是最重要的，今天你能记住，明天甚至更长时间可能会遗忘，关键是你能借助今天学习的画图法去找到规律，题目会变，但只要掌握了思想方法，任何题目都万变不离其宗.正所谓是“授人以鱼，不如授之以渔，授人以鱼以救一时之急，授人以渔则可解一生之需”.

数学思想方法是数学的灵魂和精髓.在数学广角内容的教学中，教师要引导学生进行合作交流，在解决问题的过程中感悟数学思想方法，让学生经历探究知识的整个过程，体验数学思想方法的形成过程;在巩固运用中提炼数学思想方法，以促进学生实现数学知识的完整建构及思维水平的有效提升.掌握数学思想的精髓不可能一蹴而就，需要我们在学习过程中有意识地、潜移默化地进行渗透，做到“随风潜入夜，润物细无声”.