基于滑模变的汽车横摆力矩控制研究

杜显晖

（江铃股份有限公司车架厂，江西 南昌 330000）

引言

近年来，基于横摆力矩控制的汽车稳定性研究越来越受到学者们的重视。横摆力矩的控制性能好坏直接影响到汽车驾驶的稳定性和平顺性。针对上述问题，学者们提供了各种汽车横摆力矩的控制策略。经典的方法有PID 控制、模糊控制、最优控制和滑模变控制等。其中，滑模变结构控制具有较强的鲁棒性和抗干扰性，特别适合于非线性系统的控制。由于汽车具有非线性的特性和外部具有多种干扰，故采用滑模变控制器来对汽车的横摆力矩进行控制是非常合适的。本文使用滑模变控制器对汽车的横摆力矩进行控制，首先介绍了滑模变控制器的基本原理，再在汽车系统动力学模型的基础上，使用滑模变控制器对汽车的横摆力矩进行控制，最后用汽车系统动力学仿真软件carsim 对基于滑模变控制的汽车横摆力矩进行动力学仿真，仿真结果证明了本文方法的有效性。

1 滑模控制的原理

设某非线性系统的动力学方程为：

其中，x为状态变量。

（1）通常点——如图中A 点所示（2）起始点——如图中B 点所示（3）终止点——如图中C 点所示。其中C 点即终止点在滑模变控制中为关键点。并称在切换面s=0 上所有终止点的区域为滑动模态区，简称为滑模运动。

当只有在切换面上的点全是终止点时才能使用滑模控制，则在切换面s(x)=0 附近时，有：

式（2）为滑动模态存在的条件。

如果系统的某一点再离切换面很远处，处在状态空间的任何一个地方，滑模面必须要能将所有切换面外的状态点都吸引进入切换面，所以滑动模态的全局到达条件如式（3）所示，其中x可为任意值：

基于式（1）~（3），定义滑模函数：

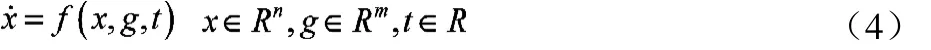
在切换函数如下所示：

控制函数可写为：

2 基于横摆力矩稳定性的滑模控制器的设计

汽车是一种机械结构负载的强耦合非线性系统，在汽车运行过程中，不大可能将所有的物理量都计算出来，只能选取较为关键的量进行控制。其中，横向运动和侧向运动对汽车稳定性的影响较大，汽车在横向运动时会产生侧偏的横向角度，如果横向侧偏角度过大，汽车就会发生翻车的危险。同样，当汽车的发生了纵向运动并且偏离目标值太大，汽车就会产生质心侧偏角。如果汽车的质心侧偏角也过大，那么同样会影响车辆的正常行驶。综上所述，将汽车的横摆侧偏角和质心侧偏角作为控制目标，使用滑模变控制器对汽车的整车动力学特性进行控制。

基于汽车横摆力矩稳定控制的滑模控制器的步骤为：首先建立整车理想模型，整车理想模型中的输入为车轮转角δ以及整车车速u，输出为质心侧偏角β以及横摆角速度γ；滑膜控制器的输入信号是β'与β之间的误差信号，记为（β'-β）、以及γ'与γ之间的误差信号，记为（γ'-γ），输出信号是是整车的横摆力矩Mz。当横摆力矩计算完毕后，根据横摆力矩进行转矩分配，从而保证汽车可以稳定的驾驶。

滑模控制器的切换面为：

对切换面s求导：

则汽车的横向动力学方程为：

可写成：

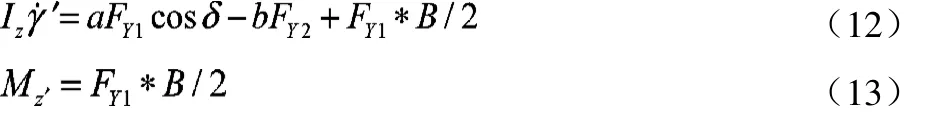
最终可得横摆力矩Mz应设置为：

3 仿真结果分析

图1 车辆转弯行驶的方向盘转角

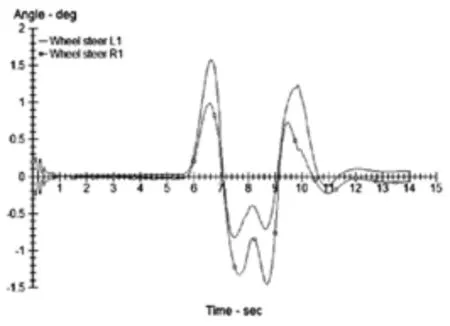
图2 车辆转弯时的车轮转角

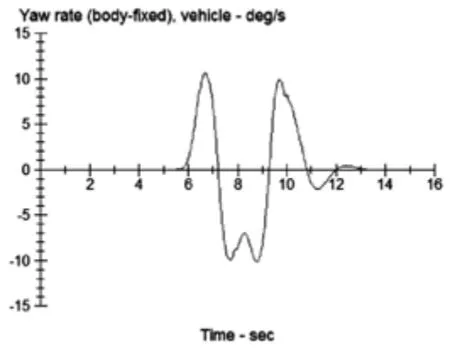
图3 车辆转弯时的横摆角速度

使用汽车系统动力学软件carsim 进行上述理论的仿真。仿真参数设置为：汽车的总质量为789 公斤，车轮半径R为0.292 米，汽车质心与前轴的轴距1.103 米，汽车质心与后轴的轴距1.244 米，汽车质心高度0.54 米，弹簧承载的质量747公斤。

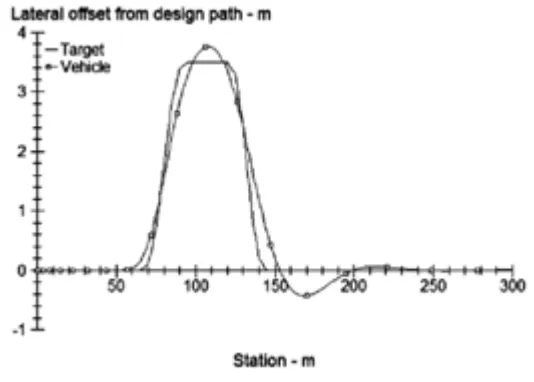
图4 车辆双移线实验时的行驶轨迹

图1 、图2 和图3 分为转矩分配系统控制的情况下车辆转弯行驶的方向盘转角、车轮转角和横摆角速度的变化曲线。图4 为车辆双移线实验时的行驶轨迹。可以看到，使用滑模变控制器可以对汽车横摆力矩进行有效的控制，从而保证了整车转向时的稳定性。

4 结论

本文使用滑模变控制器对汽车的横摆力矩进行控制，从而保证了整车行驶的稳定性。介绍了滑膜变控制器的基本理论，设计了基于横摆力矩稳定性的滑膜变控制器，并在汽车系统动力学软件carsim 上进行了仿真，仿真结果证明了本文方法的有效性。