基于悬垂平板偏转角的明渠流量估算模型及验证

王文娥，张维乐，胡笑涛，谢祥薇，杜 村，何君岩，徐 茹

(西北农林科技大学旱区农业工程教育部重点实验室，杨凌712100)

0 引 言

灌区量水技术作为实现灌区水资源优化配置和现代化农业用水管理的基本手段，为灌区用水的水费收取提供依据，提高农户节约用水意识[1-6]。置于明渠中可定轴转动的平板制作方便，测流时造成的水头损失小，水体冲击平板造成的角度偏转可以用来估算流量。目前关于平板绕流的研究多以完全浸入流体中平板的运动为主，探究放置平板攻角、雷诺数、平板尺寸参数等对其尾涡脱落特性，绕流阻力大小及阻力系数的影响。贾文超[7]根据流体力学基本理论，改进双向流固耦合算法，依次对二维平板、二维翼型、三维翼型的涡激振动特性作出分析，对频率锁定现象进行研究。秦义[8]通过流固耦合的方法，分析了平行于来流与垂直于来流放置转动板以及这两种板的组合板在高雷诺数下，不同运动频率和振幅下的旋转振荡绕流问题。张青山[9]分别在水槽和风洞中对平板分离再附流动的流场进行细致的试验测量，研究了不同弦厚比下平板分离再附流动的非定常特性和隐藏在分离剪切层内的大尺度旋涡结构的发展变化以及其与壁面脉动压力之间的联系。姜海波等[10]根据垂直平板绕流阻力和对称薄翼型全攻角绕流试验，研究得到平板大攻角放置时绕流总压力与升力和阻力分量系数与攻角的半经验计算公式。

对于平板绕流装置的研究，目前多从力、动量和量纲的角度进行研究，拟合得到经验公式。Tariq等[11-13]研究绞杆在水中的偏转现象，得到半经验平均流速关系式，并对细杆速度系数的影响因素进行分析；刘力奂等[14-15]根据泵站拍门受力计算理论，提出半经验角度流量关系式，并对其中待定流量系数取值进行验证。王军等[16-17]设计板式测流设施，并对半经验公式中的待定系数影响因素进行分析。石先德等[18-19]对摆杆式测流装置进行水力性能试验研究，结合数值模拟对其测流精度进行分析。中国北方灌区渠道底坡缓，灌溉水流多泥沙，在保证量水精度要求的条件下需采用结构简单、过流能力强、水头损失小的量水设施；平板量水设施施测简捷，过流能力强，但受制于渠道体型、坡度、平板本身材质等因素，使其缺乏适用性广泛的流量计算模型，难以广泛应用灌区量水。因此，本文从绕流理论和闸孔出流2个角度出发，在U形和矩形渠道进行原型试验，对悬垂平板在绕流中的受力做出分析，由于板后绕流存在水位差，浮力可以看做静水压力一部分，所以仅将升力简化为静水总压力竖直分力，结合原型试验，验证渠道流量与悬垂平板偏转角的关系式；基于前人对弧形闸门过流计算及自动闸门的研究[20-27]，观察试验水流流态，提出以闸孔出流流量计算模型为基础的半径验流量公式，旨在为平板量水装置的实际应用提供理论依据。

1 理论分析

在实际流体发生绕流过程中，绕流物体所受水流作用力可以转化为竖向升力F与水平绕流阻力R。绕流阻力由摩擦阻力和压差阻力构成。摩擦阻力主要由物体表面边界层中水体运动状态决定，由水体的黏滞力主导。压差阻力大小是由绕流物体形状决定，由于平板为非流线型物体，在水体绕经平板时，在平板的边缘会发生边界层的分离，从而导致尾涡脱落，由于绕流的能量损失及压能对动能的补偿，使板前后出现压差形成阻力。本文试验中明渠流的雷诺数较大，黏滞力作用小，摩擦阻力对于计算结果影响较小，故忽略。通过前期试验观察，水体绕过平板时，平板前后会形成明显的水位差，故假设升力是静水总压力垂直分力（压力体），研究在绕流现象中偏转角度和来流量之间的关系。

1.1 力矩平衡与动量方程

于明渠渐变流中安置悬垂薄平板（薄平板形状和渠道横断面尺寸相似，以U型渠道为例，见图1），平板可以绕固定轴O自由转动，薄平板在重力G，绕流阻力R和竖向升力F作用下，绕轴O偏转角度α，达到平衡。

图1平板受力分析Fig 1.Schematic diagram of stress analysis of plate

本文在计算升力时，将其简化为竖直向上水压力，F的值与压力体大小有关，压力体由板前后水位差产生的竖直分力F2-F3（图2灰色部分）组成（统称为假设1）：

升力F：

升力产生力矩MF:

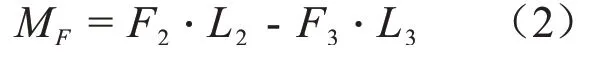
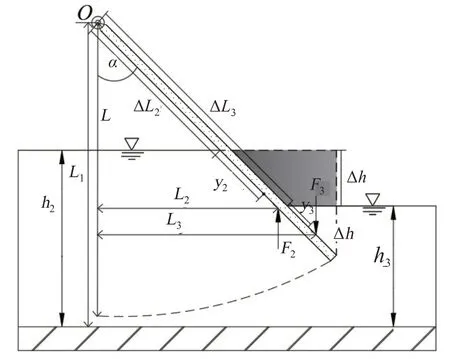
图2 升力F组成Fig 2 Composition of lift force

其中：

板前水深h2产生竖直方向静水压力F2：

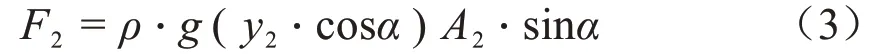
F2对轴O的力臂L2：

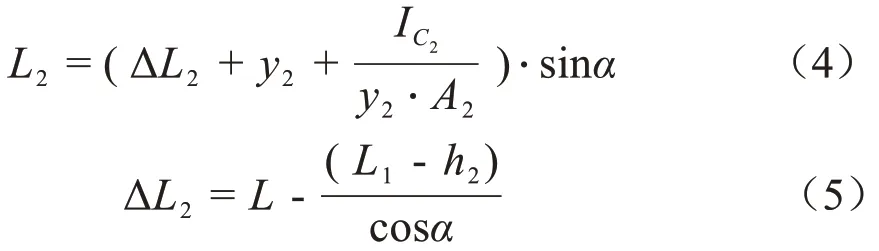
式中A2为平板迎水面浸入水体的面积，m2；α 为平板偏转角度，（°）；ρ 为水的密度，103kg/m3；y2为A2形心沿板偏转方向延伸至板前水面的直线距离，m；IC2为A2对通过其形心垂直于水流方向上的惯性矩，m4；h2为平板前稳定水深，m，L 为平板末端到轴O 的距离，m；L1为渠底到轴O的垂直距离，m；ΔL2为L 与平板迎水面没入水下长度之差，m；g为9.8 N/m2。

板后水深h3产生竖直方向静水压力F3：

F3对轴O的力臂L3：

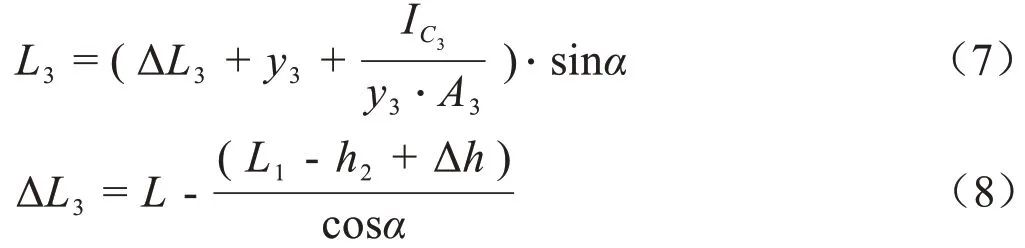
式中A3为平板背水面浸入水体的面积，m2；y3为A3形心沿板偏转方向延伸至板前水面的直线距离，m；IC3为A3对通过其形心并与垂直于水流方向上的惯性矩，m4；h3为板后水深，m，L 为平板末端到轴O 的距离，m；L1为渠底到轴O的距离，m；ΔL3为L与平板背水面默入水下部分之差，m。

绕流阻力R对轴O的力矩MR：

式中R 为绕流阻力，N，并假设作用点在平板迎水面浸入水体面积A2形心上，LR是MR力臂，m。

重力G对定轴O的力矩MG：

式中G为平板重力，kg；LG是MG力臂，m。对平板列力矩方程：

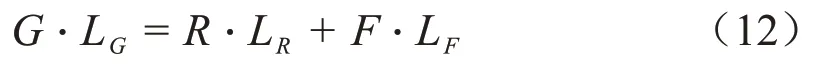
式中LF代表升力F产生力矩MF的力臂，m。

选取断面1-1、4-4间水体为控制体，当流量稳定后，控制体内水流运动可视为恒定流。故动量方程：

式中v1、v4分别为渐变流断面1-1、4-4 的平均流速，m/s；P1、P4分别为断面1-1、4-4的动水压力，N；hc1、hc4分别为过水断面1-1、4-4 的形心点水深，m；A1、A4为过水断面1-1、4-4 的面积，m2。由于两断面水流流线近似平行，动水压力取为静水压力：根据流体中点应力状态分析[28]可知，理想流体一点压强任意方向大小相等，且与黏性流体中平均点压强之差，明渠水流为不可压缩流体，故，所以。μ为流体黏性系数，λ为膨胀黏性系数。

根据式（2）、式（9）～式（15）得到式（16）

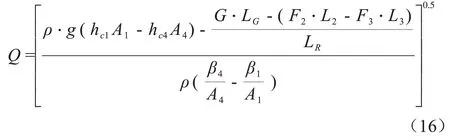
式（16）中，β1、β4为动量修正系数，一般渐变流中动量修正系数值约为1.02～1.05[28]，为简化计算，取值为1。由于所选控制体长度较短，忽略渠底对水流的摩擦阻力，并取上游水位与板前水位相等。由分析过程知，当渠道断面形状，平板密度及厚度已知时，渠道来流量与平板偏转角度具有一一对应关系。

对式（16）进行量纲分析，如式（17）为所示，满足量纲和谐。

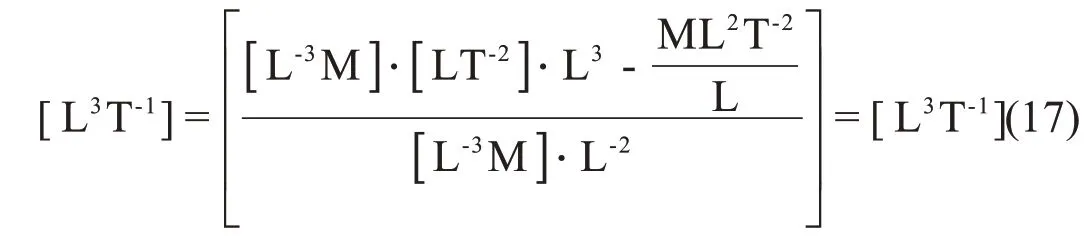
1.2 闸孔出流流量计算模型

闸孔出流水力计算是在一定闸前水头下计算不同闸孔开度时的泄流量，而闸孔出流流态影响着流量系数的取值，正确分析流态特征，确定出流条件对流量的准确计算有着重要意义。在试验时发现平板后水流流态与淹没出流下的闸孔出流流态相似，因此以闸孔出流流量计算模型为基础，拟合得到流量系数的经验表达式，得到流量与偏转角度的半经验关系式。

对上下游渐变流断面列能量方程[28]得：

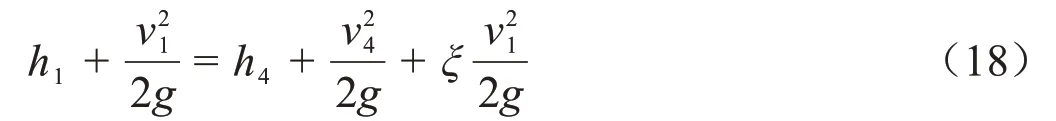
式中h1为上游渐变流断面水深，因上游水深与板前断面水深相近，默认相等；h4为下游渐变流断面水深，m；v2，v4分别为断面平均流速，m/s；ξ为局部水头损失系数。

1-1断面处水流平均流速:

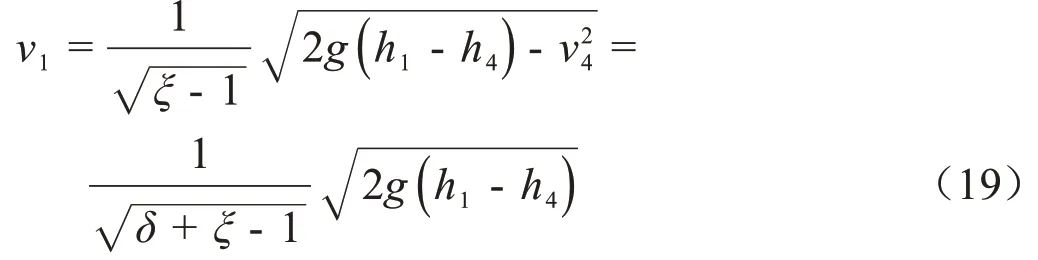
开度e：

式（19）～（20）中e为偏转时平板开度，m；δ=v4/v1。

式中A1为1-1 断面中平板部分水流过水断面面积，m2；μs为流量系数；Q为总流量，L/s；b为矩形渠道宽度，m。

2 原型试验

2.1 试验布置

试验系统（见图3）主要包括稳水格栅，水泵，三角形量水堰，流量调节阀门，电磁流量计，尾门，U形渠道，U形平板，矩形渠道，矩形平板等。试验测点布置图见表1。

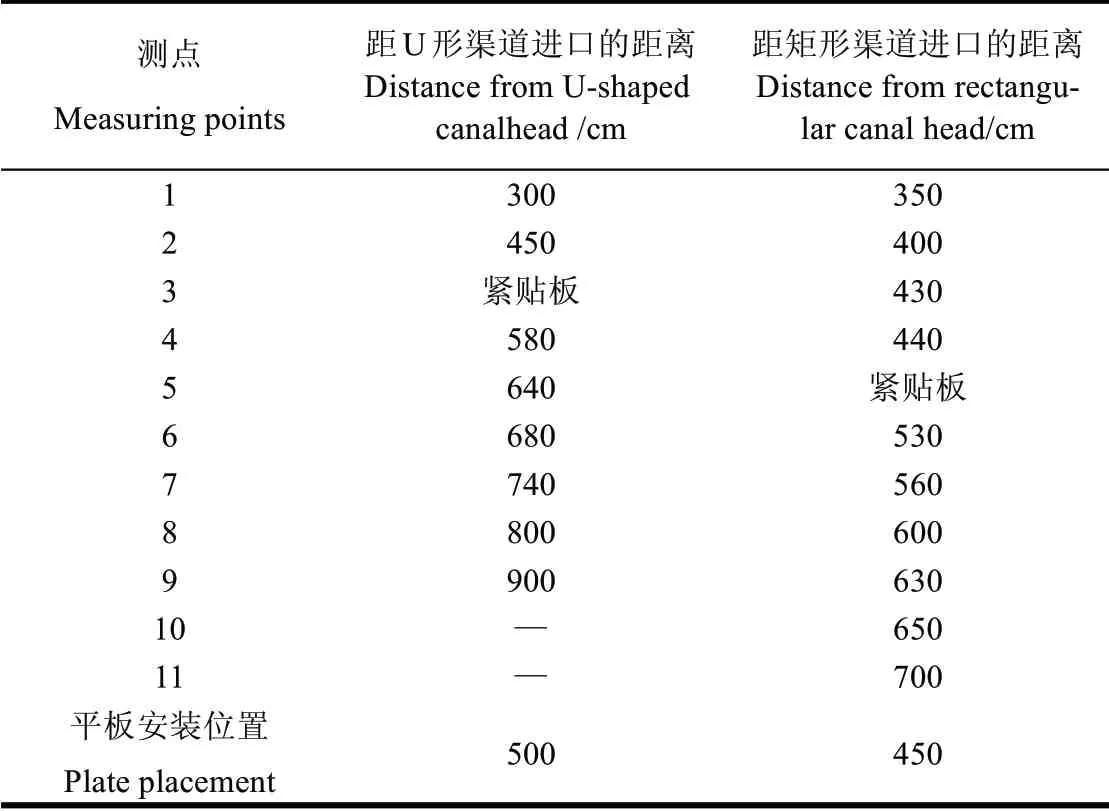
表1 测点布置Table 1 Layout of measuring points

U形渠道为标准D40渠道（图3），由有机玻璃材料制成，渠道坡度5×10-3，综合糙率0.011；U形平板为铝制，板厚8 mm，为减小不必要误差，安装时使平板顶部和渠道顶部平齐，平板边缘距渠道侧壁及底部均为1 cm。

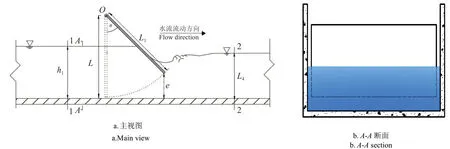
图3 渠道横断面示意图Fig 3. Schematic of canal section

矩形渠道由混凝土衬砌而成（图4），底坡是平坡，综合糙率0.014；矩形铝制平板板厚5 mm，安装时使平板侧边缘距离渠道侧壁1 cm，板底距渠底5 mm。

平板偏转角度用电子数显角度尺测量，精度0.1°；断面水深用水位测针测量，精度0.1 mm。U 型平板试验流量范围9～44 L/s，共选取9个流量，每种工况流量相差5 L/s左右；矩形平板试验流量范围为10～40 L/s，共5 种流量，每种流量下改变尾门调节水深4次，共20种工况；每种流量下水深及偏转角测量多次。

2.2 结果与分析

2.2.1 流量-偏转角度关系验证

选取所测角度及水深代入式（16），得出理论值。文献[29]在计算升力时，将板体体积产生的浮力加入到压力体的计算中（统称为假设2）。图5a给出了平板在U 型渠道中2 种假设下，实际流量及计算流量的相对误差。图5b给出的是矩形渠道假设1计算流量与实测流量的相对误差。对于U 型渠道，2 种压力体假设均适用于流量计算，除流量较小时，相对误差超过10%，其余工况流量大于17 L/s 时，相对误差均在5%左右。对于矩形渠道，经验证，应用假设2计算压力体时(图5c)计算流量与实际流量相对误差较大，应用假设1 计算压力体时，当流量在10 L/s 左右时误差会偏大，除个别工况计算误差大于10%外，大部分工况下计算误差均小于10%。从计算结果看出，本文中所提假设1适用性强于假设2。

2.2.2 闸孔出流流量计算模型

闸孔出流流态不同影响着流量系数的取值，经计算发现板后断面傅汝徳数始终小于0.5，板后水流流态与完全淹没出流下水流流态相似[20]，故采用闸孔出流淹没出流流量计算模型进行半径验拟合。联立式（20）和式（21）：

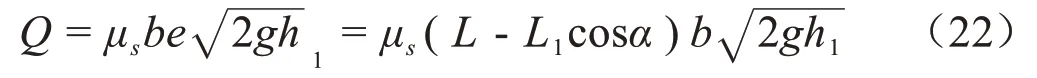
式中μs为流量系数；b 为矩形渠道宽度，m；e 为开度，m；L为轴O到装置末端距离，L1为轴O到渠底距离，m。

通过图6 可以看出所有工况下的（h1/h4，us）密集的分布在1条曲线周围，得出流量系数计算模型：

图4 试验布置图Fig.4 Layout plan

式中k、b为参数，由板型和渠道尺寸决定。

由此拟合得出半径验流量公式：

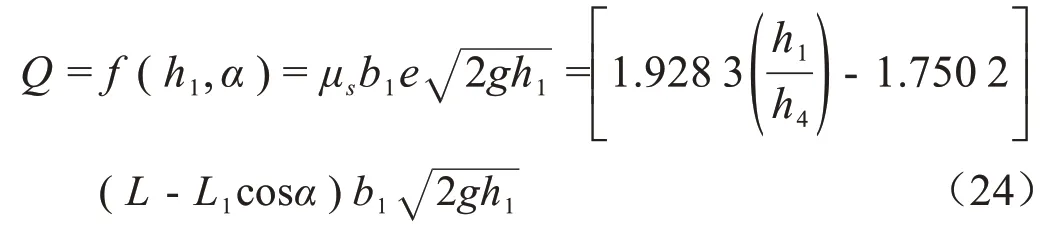
将计算值与实测值对比（图6b）。结果表明：二者之间最大误差不超过18%，大部分工况下计算误差在10%以下。公式中没有出现板后水深h3，相比理论模型，在实践中应用性更强。

2.2.3 平板偏转角度水深关系讨论

图7 为矩形渠道试验工况下板前后水深比、上下游水深比与偏转角度α的关系。

从图7可以看出，同一流量下，h1/h4、h1/h3分别与偏转角度α 有着单独的函数关系，h1/h4与h1/h3随着平板偏转角度的增大而减小，但减小幅度变缓。对于不同流量，随着流量的增大，h1/h4与h1/h3随着角度增大而增大。由第一种流量关系式的推导可知，Q可转化为h1与角度α的函数，其形式可表示为Q=f(h1,α)，这与文献[11]得出的结果类似，可以以此作为切入点，对平板量水设施流量角度关系进行更进一步探究。

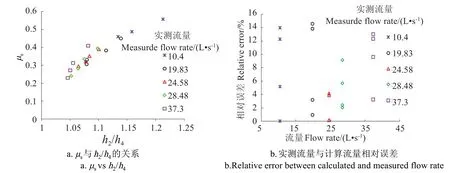
图6 经验公式验证Fig 6 Verification of empirical formula

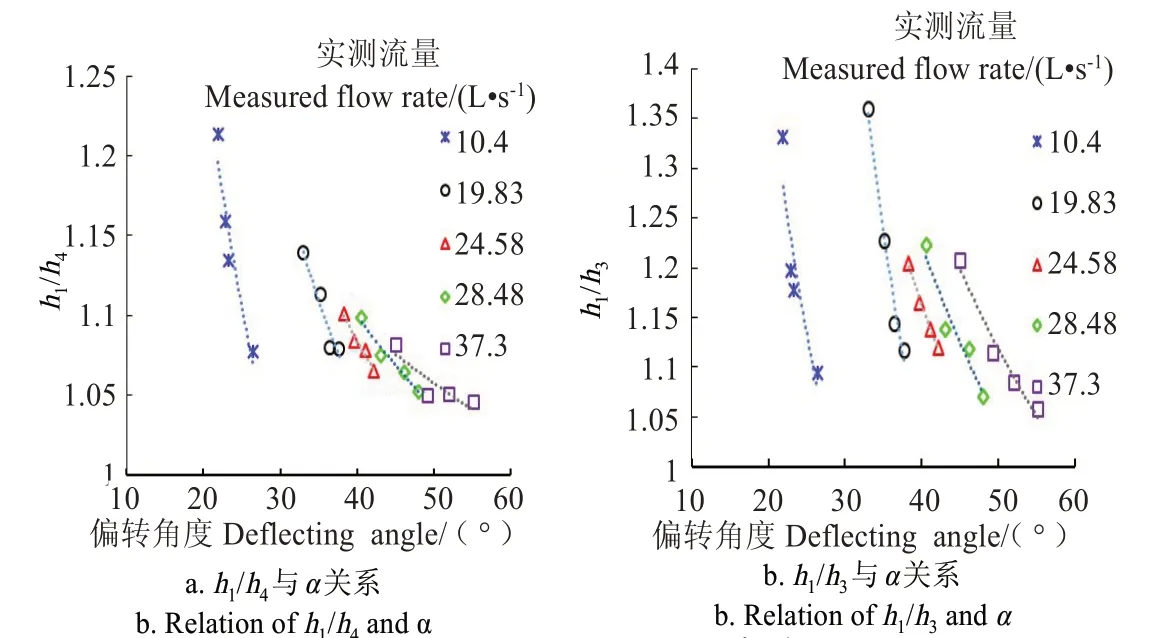
图7 水深比与流量关系Fig 7 Relationship between depth ratio and angle

3 结 论

1）根据升力简化为竖直方向静水压力设想，提出2 种压力体计算假设，根据动量定理与力矩平衡公式得到了流量、角度、水深三者的理论关系式，并验证假设合理性。对于U 型渠道，2 种压力体假设均适用于流量计算，除小流量工况验证时相对误差大于10%，当工况流量大于17 L/s时，相对误差均在5%左右；对于矩形渠道，仅假设1适用流量计算，假设2不成立。应用假设1计算压力体时，当流量在10 L/s左右时误差会偏大，除个别工况计算误差大于10%外，大部分工况下计算误差均小于10%。因此本文提出的假设1适用性更强，测流范围在10～44 L/s。

2）由于板后水流流态与完全淹没出流流态下水流流态相似，根据闸孔出流流量公式建立半径验计算模型，拟合得出半径验流量公式。结果表明：计算流量与实测流量之间最大误差不超过18%，大部分工况下计算误差在10%以下。公式中没有出现板后水深h3，在实践中应用性更强。

3）同一流量下，板前后水深比h1/h4、板前与下游水深比h1/h3分别与偏转角度α 呈现出单独的函数关系，h1/h4与h1/h3随着平板偏转角度的增大而减小，但减小幅度变缓。对于不同流量，h1/h4与h1/h3随着角度增大而增大，但增大幅度变缓。

本文从2 个角度对平板量水的测流机理进行探讨。由于在试验中无法在同一时刻对所涉及物理参数进行同时测量，理论模型中下游水深h4对计算结果影响较大，应考虑在公式中加入“随机项”及修正函数来对其进行修正。

水力自动闸门是根据上游来水量及水位变化,利用水压力产生的推动力矩与闸门及配重产生的回复力矩进行自动启闭，实现水流的自动调节的闸门。类似挡板结构的自动闸门在国外灌区的应用已取得一定研究成果。闸门宽度并非与断面宽度一致，采用闸孔出流公式和宽顶堰流公式分别对闸门下流量和两侧绕流流量进行半经验计算，既能提高过流能力，也可以实现流量的测控。但是中国北方渠道底坡较平缓，灌溉水流含沙量大，闸前堰坎的存在会造成严重的泥沙淤积，影响渠道的输水能力。本文设计平板板型与断面大小一致，可参考国外挡板闸门结构，将运动水流分区进行分析，并且改变平板收缩比，将板后形状改为圆弧形，添加平衡锤，使得板后水压力对圆心力矩为0（水压力垂直于作用圆弧面，对圆心取矩），进而通过力矩平衡原理进行简化计算。该量水设施有望结合电子设施实现对渠道流量的远程动态监测。目前该量水装置仅在清水条件下进行了试验，当水流含有泥沙时，泥沙含量会使平板受力有所变化，使平板偏转角与流量的关系与清水工况不同，假设合理性尚需进一步试验研究。

该文仅针对当平板尺寸与渠道等大时，对平板偏转角与来流流量关系进行探讨，计算模型仍需进行完善。当平板面积与渠道尺寸不一致时，水流绕流作用加剧，平板角度流量影响因素均不相同，仍需对模型中假设进行进一步验证。