基于模糊Borda组合模型评价番茄产量及品质对水肥供应响应

胡田田，何 琼，洪 霞，刘 杰，李鸿祥，冯璞玉，王 丽，杨硕欢

（西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌，712100）

0 引 言

随着生活水平的日益提高，人们越来越多地关注蔬菜的品质。通过农业生产管理措施的改善，获得兼具高产且品质优良双重特性的农产品就显得尤为重要。因而，现代温室番茄生产的水肥管理，不仅要关注产量或某项品质指标等单一目标，更要考虑产量、品质等多个目标的实现，具有多目标评价的特点。

目前，国内外建立的多目标综合评价方法已达数百种[1]，在农业方面较为常用的有层次分析法[2-3]、灰色关联度分析法[4-5]、隶属函数分析法[6-7]、TOPSIS 法[8-9]和熵权法[10-11]等单一评价方法，在番茄品质及产量-品质综合评价方面的应用，多集中在单纯的品质评价中[12-16]。由于各单一评价方法的机理不同，利用信息的角度和侧重点不同，加上评价过程中存在的人为因素，使得各方法的评价结果之间存在差异，选择任何一种方法都难以对客观事实进行全面准确地判断。

为解决多种单一评价方法结论不一致的问题，研究者提出了另一类综合评价方法，即组合评价方法，是在综合评价基本原则的指导下，遵循一定的准则和规则，采用若干能独立完成评价的方法对评价对象进行综合评价，在此基础上，再通过合理的组合算法将其评价结果进行优化组合的评价模型。这方面，主要是国内一些学者利用数学分析方面的研究成果，提出了一系列方法与模型[17-20]。目前对组合评价的研究，主要集中在组合权重、组合结果、组合方法3 方面。在组合结果方面，国内外常用的组合评价方法有Borda 组合评价模型[17]、模糊Borda组合评价模型[17]、Copeland 组合评价模型[17]以及基于整体差异的组合评价模型[21]。Borda 组合评价模型是一种少数服从多数的方法，在实践应用中以排序值作为基础进行组合；Copeland 组合评价模型在Borda 法的计算方法上进行了优化，同样根据排序值进行模型组合[22]，在实际应用中简单易懂，二者在组合单一评价模型结论排序均不涉及单一评价模型结论的权重；模糊Borda 组合评价模型同时考虑了评价值和排序值[17]，未涉及单一评价模型结论的权重，在运算方式上进行了简化，组合结论的精确性进一步提高；基于整体差异的组合评价模型选用评价值进行组合，通过对单一评价模型的评价值进行一系列的计算得出组合权限量，最大限度的利用了评价结论的信息[21]。作为一类新的综合评价方法，组合评价方法在管理科学等其他领域应用较多，对于农业领域尤其在番茄水肥管理方面的应用还鲜见报道。

为探讨组合评价方法及其在番茄产量-品质综合评价中的应用，在前期以基于整体差异的组合评价模型对番茄营养品质进行评价的基础上[23]，本文选取番茄水肥试验中番茄果实的6 项品质指标（可溶性糖、可溶性固形物、可滴定酸、番茄红素、以及维生素C、糖酸比）及产量数据，采用主成分分析法、灰色关联度法、隶属函数法和基于组合赋权的TOPSIS 模型4 种单一评价方法对番茄产量-品质进行评价，并在通过相容性检验的基础上，采用Borda、Copeland、模糊Borda 和基于整体差异的组合评价方法4 种组合评价方法，分别构建组合评价模型，通过事后检验择优，分析其综合评价值对水肥的响应，获得适宜的水肥用量区间，以期为番茄水肥管理决策提供依据与参考。

1 数据来源与分析方法

1.1 数据来源

研究资料包括番茄果实6 项品质指标（可溶性糖、可溶性固形物、可滴定酸、番茄红素、维生素C、糖酸比）及产量数据，来源于2014 年9 月—2015 年7 月在陕西杨凌大寨村进行的32 个处理的温室番茄水肥试验[23]。该试验针对长季节栽培番茄，采用滴灌施肥方式，以灌水量和氮、磷、钾肥及有机肥用量为试验因素，采用五元二次通用旋转组合设计，试验因素的5个水平及其编码值见表1。试验方案及结果参见文献[23]。经方差分析与多重比较，32 个处理间的品质及产量数据差异显著，而且，保证产量或者品质最优的水肥用量存在一定差异（表2），因此，有必要对产量和品质进行多目标综合评价，以确定多目标最优情况下水肥用量的适宜区间。

表1 试验因子实际水平及其编码值Table 1 Levels of experimental factors and their codes

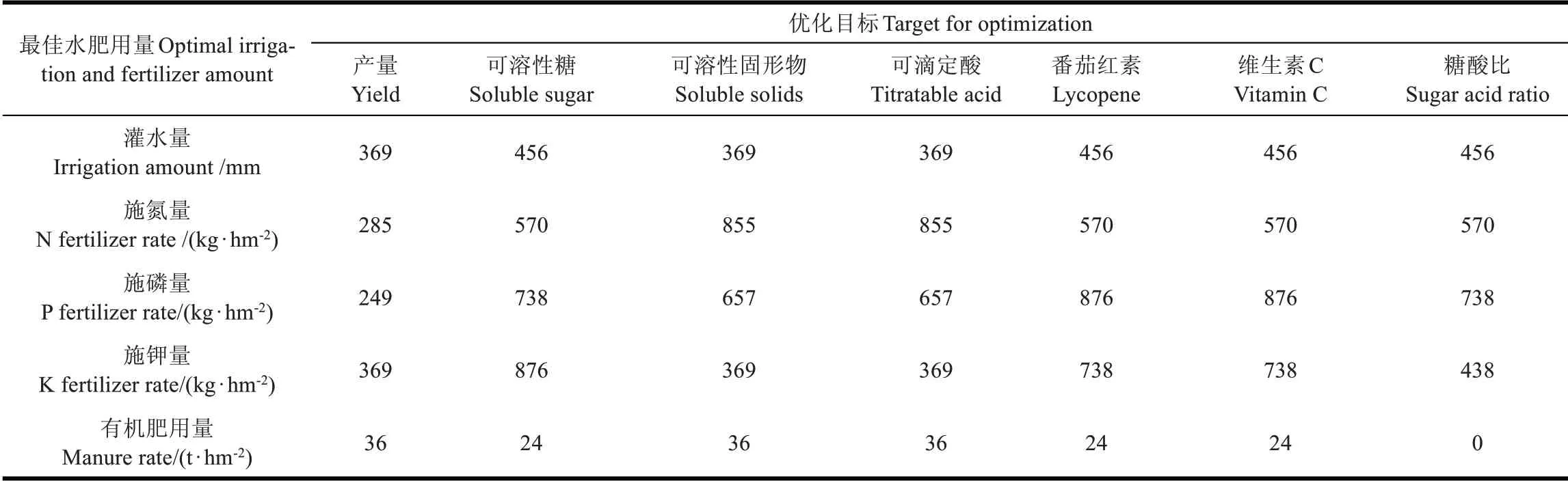
表2 不同优化目标下最佳水肥用量组合Table 2 Optimal combination of water and fertilizer under different targets for optimization

1.2 模型构建方法

参考其他研究领域的组合评价的算法，本研究中组合评价具体包括以下步骤：

1）以番茄果实品质和产量为评价指标，采用主成分分析法（principle component analysis,PCA）、灰色关联度分析法（grey relational degree analysis,GRDA）、隶属函数分析法（membership function analysis, MFA）和基于组合赋权的TOPSIS 模型（TOPSIS-CW）4 种单一评价方法分别对番茄产量-品质进行综合评价。

2）单一评价方法的评价结果能否用于组合评价，即是否具有相容性，需要进行事前检验。文中采用Kendall协和系数检验法进行事前检验[18]，该检验主要考查m 种评价方法对n 个对象的评判结果是否一致。通过讨论4种单一评价方法下的协和系数W 显示样本数据的实际符合与最大符合之间的分歧程度，当协和系数W 越接近于1，说明评价方法的相容性越高。在通过事前检验的基础上，采用Borda 评价法[17]、Copeland 评价法[17]、模糊Borda 评价法[17]和基于整体差异的组合评价法[21]（ODCA），分别构建组合评价模型，进行组合评价。若不能通过事前检验，则剔除效果最差的一种单一评价方法，重新进行上述的Kendall检验，直至所有方法通过检验。

下面简要介绍一下这4种组合评价方法：

Borda评价法

若评价认为处理Xi优于Xj的个数比Xj优于Xi的个数 多，记 为XiSXj，则 定 义Borda 矩 阵，处理Xi的得分，最后根据bi得分大小对Xi进行排序。

Copeland法

在上述Borda 评价法、Copeland 评价法2 种方法中，若出现多个处理得分相同的情况，则根据每个处理在2种方法下的方差大小进行排序，方差小者排在前面。

模糊Borda评价法

首先，计算4种单一评价方法的隶属度μij

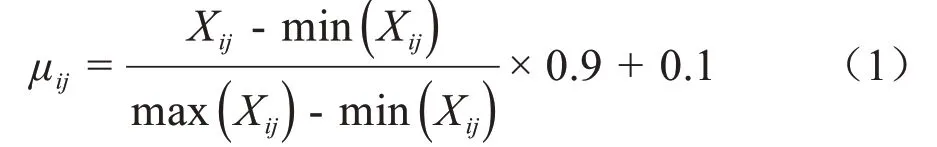
Xij代表第i个处理在第j种方法下的得分，μij代表第i个处理在第j种评价方法下属“优”的隶属度；其次，计算模糊频率

再次，计算模糊Borda数：

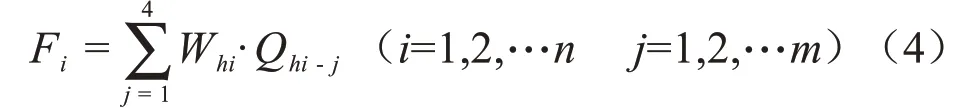
并按照Fi进行排序，其值越大，番茄产量-品质越好。

基于整体差异的组合评价方法

用矩阵A 表示n个评价对象，m 种评价方法得到的评价值(不失一般性，设n ≥3，m ≥3)

即

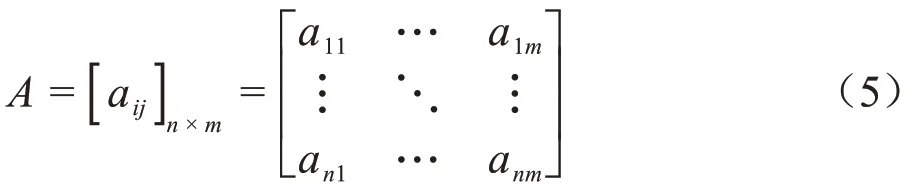
对原始多评价方法结论矩阵进行标准化处理，即

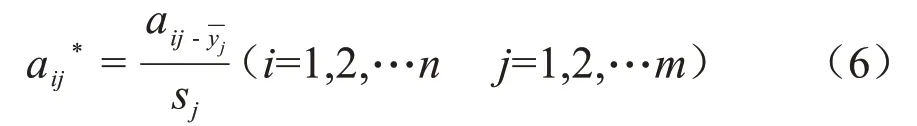
得到A；求解实对称矩阵H，H = ATA；求H 的最大特征值及相应的标准特征向量；根据标准特征向量中各分量的取值情况确定组合权向量；将权向量代入yi= λi· ai1+ λi· ai2+ …λi· aimi = 1,2,…n，计算各评价对象的组合评价值；对评价对象按组合评价值大小进行排序。

3）采用Spearman 等级相关系数检验法[18]，对上述4种组合评价方法进行事后检验。首先依据组合评价结果的排序值对组合方法和单一方法做相关性分析，若4 种组合评价的结果完全一致，则通过事后检验即可选定最优组合方法。若4 种组合评价的结果仍存在差异，则利用Spearman 等级相关系数法构造统计量t[18]，t 值越大说明该组合评价模型的性能越好，选择与原单一方法最接近的组合为最佳组合模型。

1.3 数据处理

基于博弈论的赋权和基于整体差异的综合评价采用MATLAB6.5进行计算，主成分分析法和相关性分析采用SPSS18.0完成，层次分析法所采用的权重值参照文献[14]。灰色关联度分析法、隶属函数分析法、熵权法、事前事后检验、Borda 评价法、模糊Borda 评价法以及Copeland 法均采用Excel 完成。采用DPS7.05 建立综合评价值与试验因素的二次多项式并进行寻优。水肥单因子及其耦合效应图采用Sigmaplot12.0完成。

2 结果与分析

2.1 基于单一评价模型的番茄产量-品质综合评价

以番茄果实品质和产量为评价指标，分别采用主成分分析法、灰色关联度分析法、隶属函数分析法和基于组合赋权的TOPSIS 模型4 种单一评价方法对32 个处理的产量-品质进行综合评价，评价结果见表3。从表3 可以看出，4 种方法评价值排名的标准差分布在0～6.85，且无明显的规律。32个处理中，有7个处理（1、10、16、19、21、22 和24）的评价值排名相差较大，标准差在4.0 及以上；16 个处理评价值排名的标准差介于1.0～4.0 之间；9 个处理（3、7、9、14、17、20、23、26 和27）的评价值排名相差较小，标准差在1.0 及以下。可见，4 种单一评价方法的评价结果存在较大的差异性。

2.2 番茄产量-品质单一评价模型的事前检验

4种单一评价模型序值的Kendall相关系数[24]见表4。表4表明，各单一模型评价值与其他3种间相关系数的均值在0.605～0.812 之间，表明单一模型的结果之间存在一定的相关性。其中基于组合赋权的TOPSIS 模型与其他3种方法的综合相关性最弱，隶属函数模型与其他3种方法的综合相关性最强。

进一步采用Kendall－W 协和系数检验方法进行显著性检验[23]。计算得到Kendall－W 协和系数W=0.916，则χ2= m(n - 1)W = 113.6 ≥χ20.0131=55.0，表明4 种方法具有相容性，满足事前一致性检验。

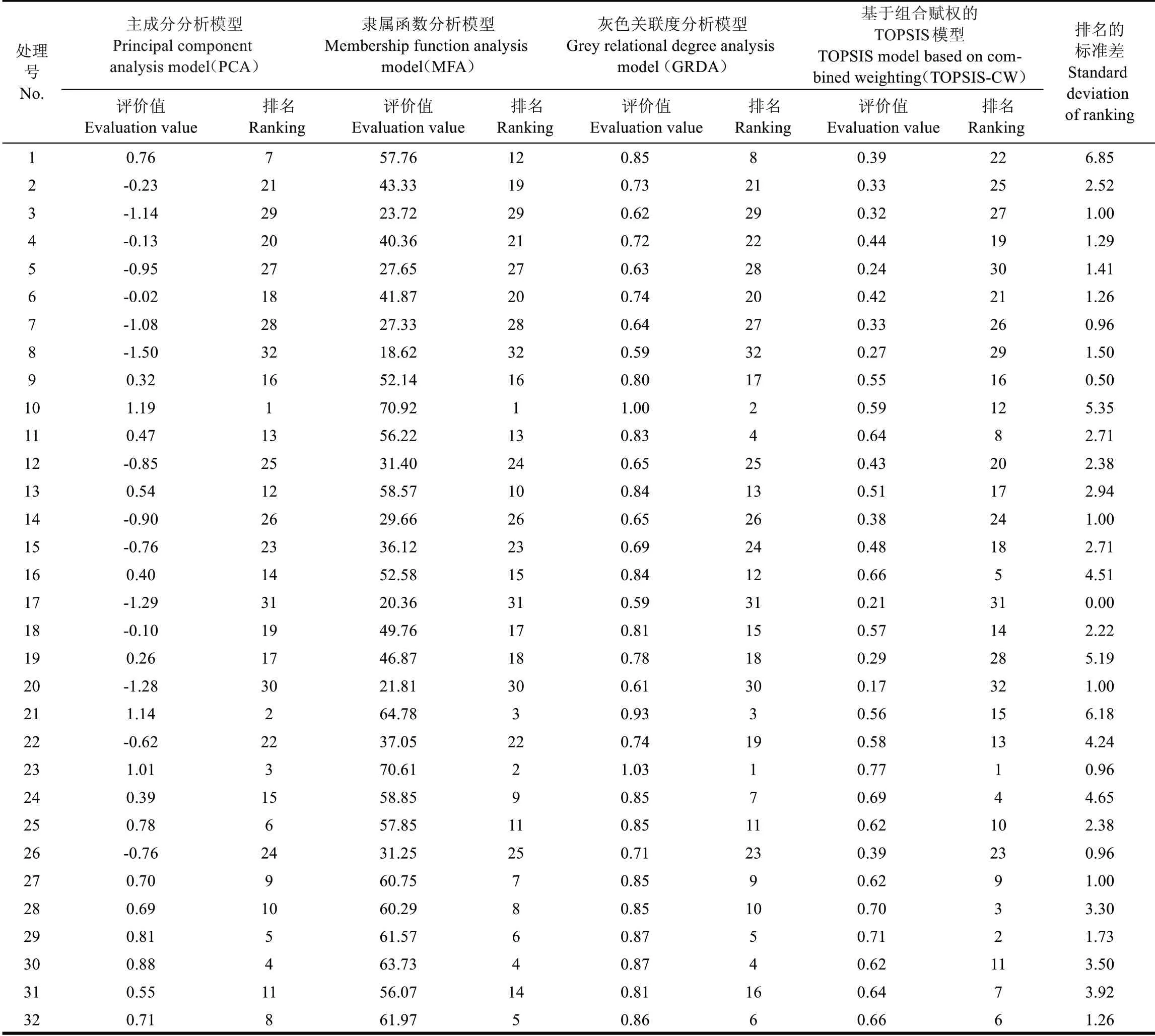
表3 单一评价模型的番茄产量-品质综合评价结果Table 3 Results of single evaluation model on yield and quality of tomato

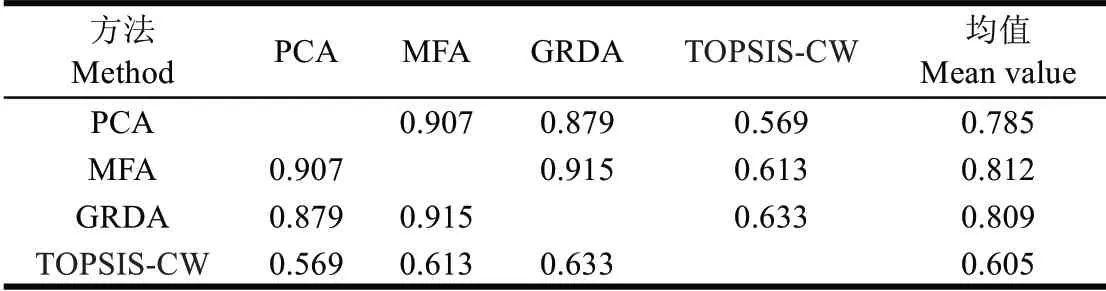
表4 单一评价模型序值的Kendall相关系数Table 4 Kendall correlation coefficient of single evaluation model sequence values

2.3 番茄产量-品质组合评价模型的构建

分别采用Borda、Copeland、模糊Borda和基于整体差异的组合评价方法对上述单一评价方法的结果进行组合，构建组合评价模型，结果见表5。32个处理中有17个评价值排名的标准差在1.0 及以下，占处理总数的50%以上；1个处理评价值排名的标准差为0，表明4种组合评价模型的评价结果有很强的一致性。

2.4 番茄产量-品质的组合评价模型的事后检验

对组合评价模型的序值与各单一模型的序值做Spearman 相关性分析[18]（表6），相关系数的均值介于0.920～0.952 之间，表明组合评价模型与单一模型的结果有很强的相关性。其中Borda 组合评价模型与各单一评价模型结果的相关性最弱，基于整体差异的组合评价模型和模糊Borda 组合评价模型与各单一评价模型结果的相关性接近，表现最强。

进一步根据组合评价模型的排序结果与原始单一评价模型排序结果的相关程度构造统计量t，取t 值最大的组合为最佳组合评价模型。4 种组合方法的检验统计量见表7。表7 表明，4 种组合评价模型的t 值均明显大于t0.01(31)的临界值，即4 种组合评价模型均通过一致性检验。模糊Borda 组合评价模型t 值最大，Borda组合评价模型的t 值明显小于其他模型，说明模糊Borda组合评价模型表现最优。因此，下面以模糊Borda 组合评价模型的评价值与水肥用量间建立回归方程，分析番茄产量-品质综合评价值对水肥供应的响应。

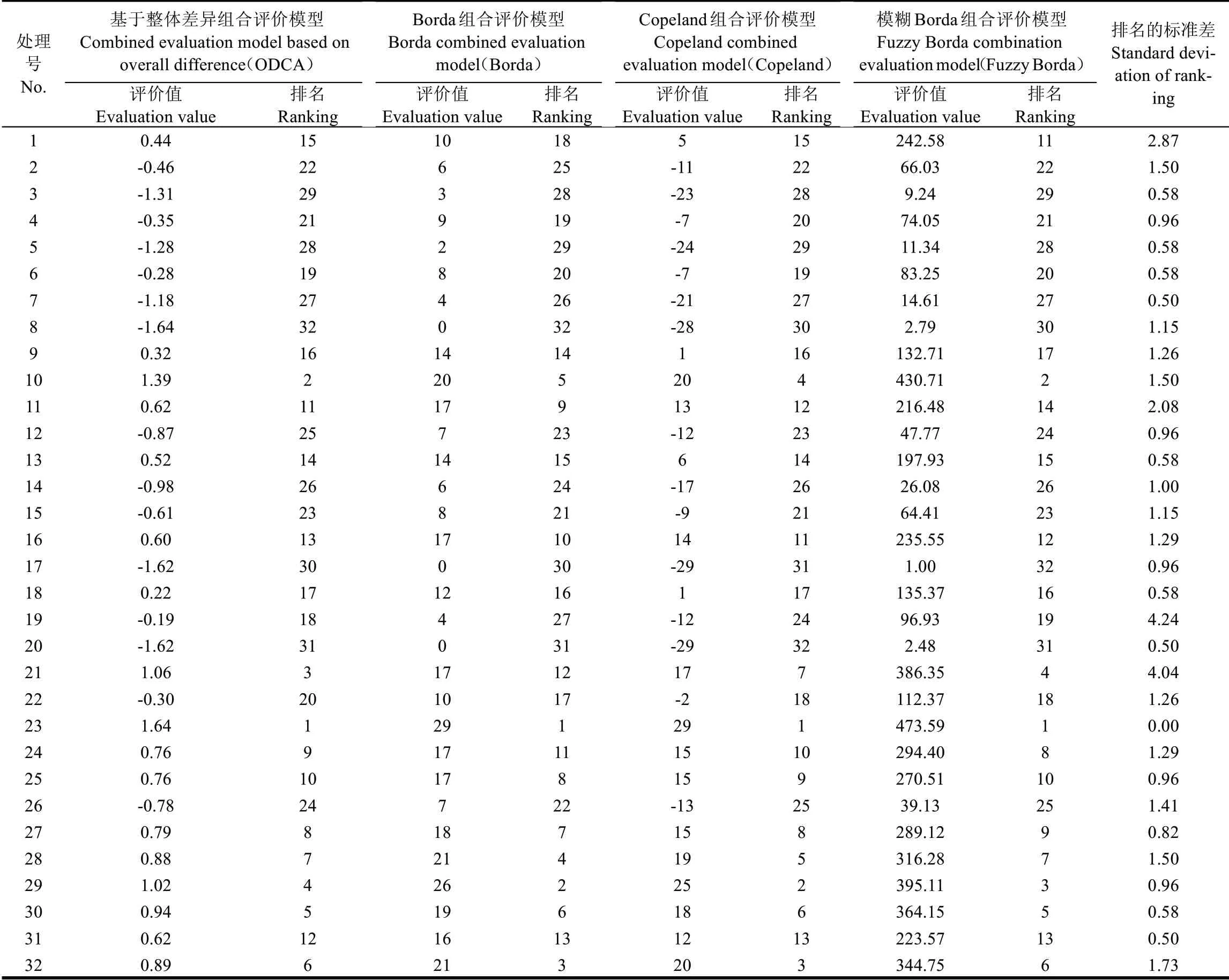
表5 组合评价方法的番茄产量-品质综合评价结果Table 5 Results of combined evaluation model on yield and quality of tomato

表7 Spearman等级相关系数事后检验Table 7 Post-test of Spearman rank correlation coefficient

2.5 基于模糊Broda 组合评价模型的番茄产量-品质评价指标对水肥用量的响应

建立模糊Broda组合评价模型确定的产量-品质综合评价值与5 个水肥因素Xi的编码值[-2，2]间的关系式，方差分析（表8）表明，回归方程的失拟性检验F1= 1.25 ＜F0.05(6,5)= 4.95，说明回归方程对试验点拟合较好；回归F2= 7.38 ＞F0.01(20,11) = 4.1，说明模型是有效的。进一步，剔除α=0.1下不显著项，得到如下简化回归模型：

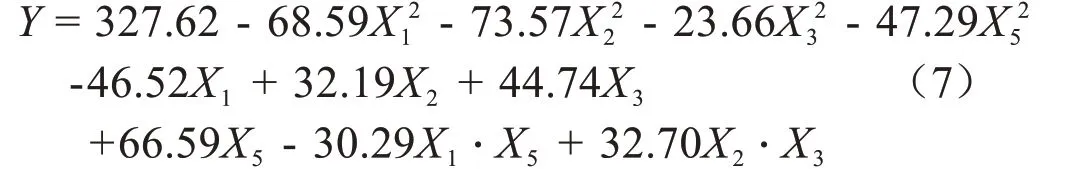
式中X1、X2、X3、X4、和X5分别为灌水量、施氮量、施磷量、施钾量和有机肥用量的编码值。

2.5.1 单一因素对番茄产量-品质综合评价值的影响

回归模型的函数变幅值Si是当其他因子固定时，某一因子取不同水平时函数值的标准差的大小，可衡量该因子对目标函数的相对重要程度，可用来比较二次模型中各因子的作用大小[25]。通过计算函数变幅值，可知各水肥因素对番茄产量-品质的影响效应：施氮量（Si=155.90）≥灌水量（Si=154.36）＞有机肥用量（Si=133.79）＞施磷量（Si=92.95）＞施钾量（Si=0）。通过降维处理，即固定其他因素为0 水平，得到水肥用量各因素对番茄产量-品质评价值的回归模型，据此可知在试验范围内，其他因素为中间水平时，番茄产量-品质综合评价值与灌水量、施氮量、施磷量和有机肥用量的关系均呈凸型二次曲线；与施钾量呈水平线，表明施钾量对综合评价值没有影响（图1）。从中可以看出，当水肥投入量均为较低水平时，灌水量和施磷量、施氮量和有机肥用量的影响效应比较接近；在超过最适量后，灌水量和施氮量均表现为明显的负效应，且前者的负效应远大于后者。

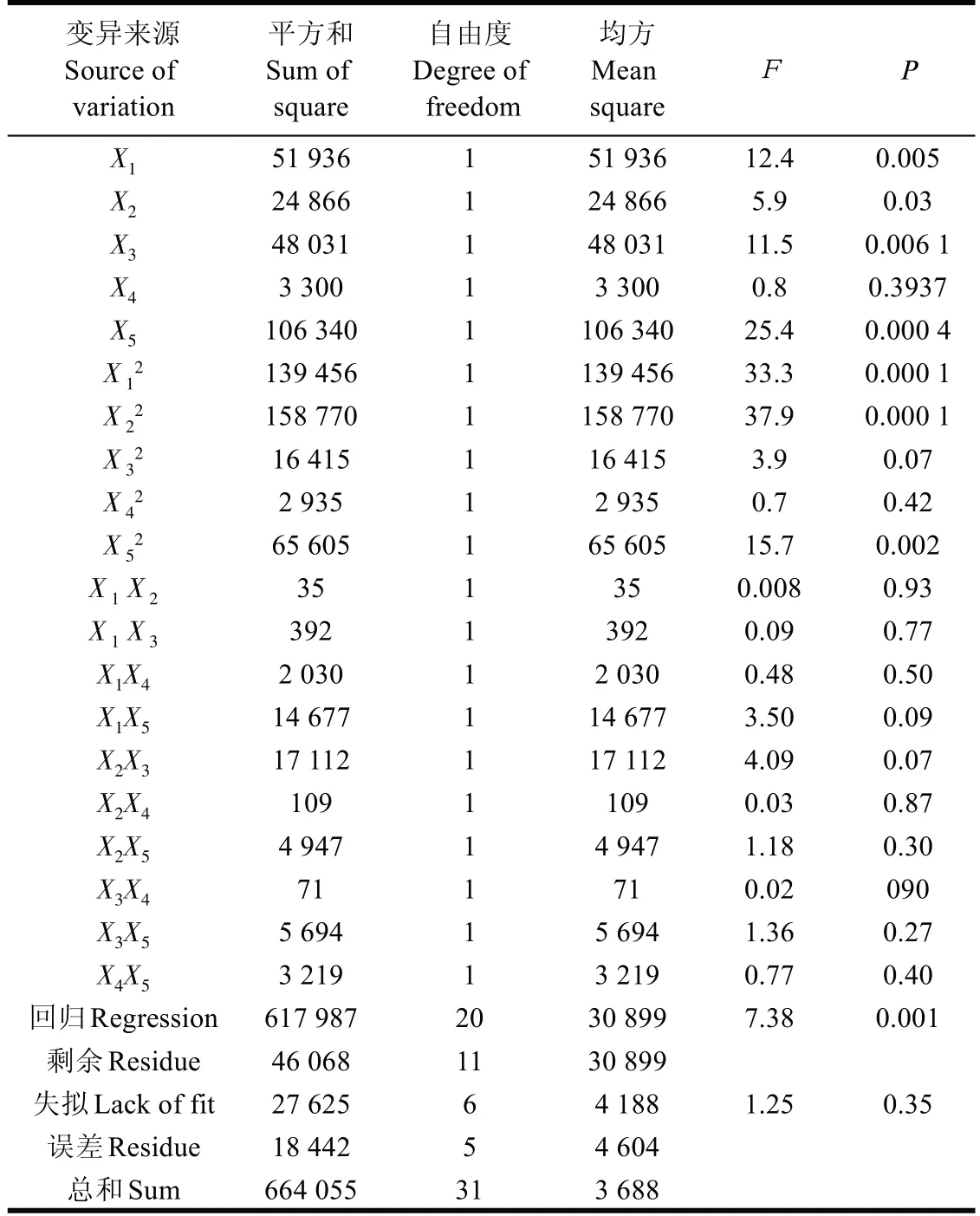
表8 模糊Broda组合评价值回归关系的方差分析Table 8 Analysis of variance on regression of fuzzy Broda combination evaluation value

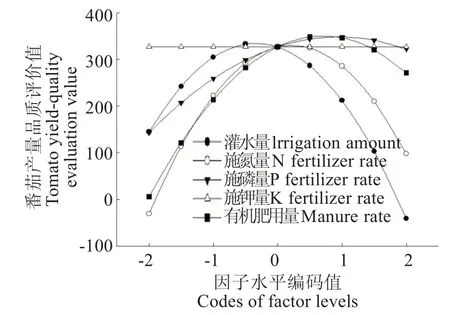
图1 单一因素对番茄品质-产量综合评价值的影响Fig.1 Effect of each single factor on evaluation value of tomato quality and yield

2.5.2 两因素对番茄产量-品质评价值的耦合效应

1)灌水量和有机肥用量对番茄产量-品质评价值的耦合效应

灌水量和有机肥用量的交互项系数为-30.29，为负效应（式（7）），即二者相互作用阻碍番茄产量-品质评价值的提高。无论灌水量处于什么水平，随着有机肥用量的增加，评价值先增大后减小；同样，不论有机肥用量为什么水平，随着灌水量增大，评价值仍表现为先升高后降低（图2a）。计算可知，灌水量为410 mm（接近中间水平），有机肥用量在32～38 t/hm2时（处于中间至较高水平），番茄产量-品质评价值达到最大值369；在灌水量和有机肥用量均处于最低水平（分别为282 mm和0 t/hm2）时，番茄产量-品质评价值达到最小值-297，比最大值降低了180%。表明灌水量和有机肥用量合理施用能同时提高番茄的产量和品质，过高或过低均不利于番茄产量品质的提高。

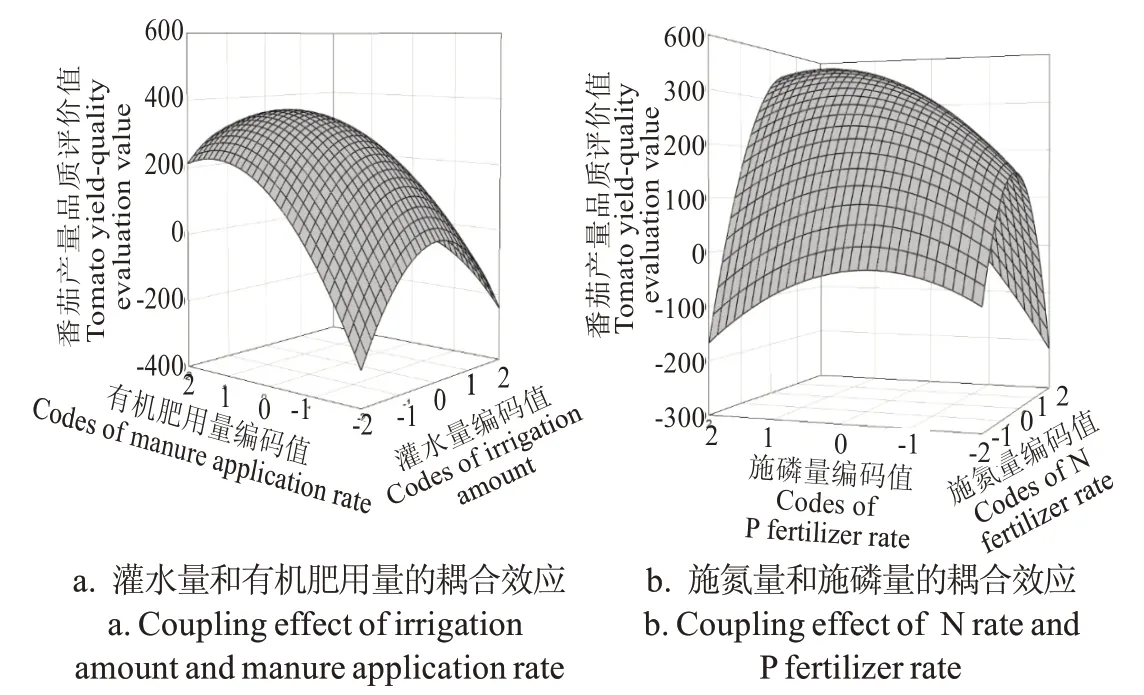
图2 两因素对番茄产量-品质评价值的耦合效应Fig.2 Coupling effect of 2 factors on comprehensive tomato yield and nutrition quality

2)施氮量和施磷量对番茄产量-品质评价值的耦合效应

施氮量和施磷量交互项系数为32.70，呈正效应（式（1）），即二者相互作用促进番茄产量-品质综合评价值的提高。图2b 表明，当施氮量位于低水平和中间水平时，随着施磷量的增加，评价值呈先上升后下降的趋势；当施氮量为950 kg/hm（2较高水平）时，随着施磷量的增加，评价值呈线性增大趋势，而且，随着施氮量的增加，直线斜率增大，番茄产量-品质综合评价值随施磷量的增加幅度变大。不论施磷量水平，随着施氮量的增加，评价值均先增大后减小低，而且，随着施磷量增大，抛物线的最高点向施氮量变大的方向移动。计算可知，氮肥用量为722 kg/hm（2介于中间至较高水平），施磷量为730 kg/hm（2介于较高至高水平）时，番茄产量-品质的评价值最大，为365左右；当施磷量处于最低水平时（不施磷）、施氮量处于最高水平（1 140 kg/hm2），番茄产量-品质的评价值最小，为-217 左右，比最大值降低了160%。可见，增加施磷量、合理配施氮肥有利于番茄产量-品质综合评价值的提高。

2.5.3 基于产量-品质综合评价值的最佳水肥用量

为使最大番茄产量-品质评价值的水肥用量决策建立在可靠的基础上，根据式（7），可得到3 125个理论组合方案，其值分布在-850～350，其中小于-750的组合方案20套，-750～-650 的方案40 套，-650～-550 的方案95 套，-550～-450 的方案125 套，-450～-350 的方案260 套，-350～-250 的方案300 套，-250～-150 的方案450 套，-150～-50 的方案430 套，-50～50 的方案425 套，50～150 的方案385套，150～250 的方案400 套，250～350 的方案160 套，大于350 的方案35 套。表明较高的番茄产量品质综合评价值在-250～-150 的频率分布较大，相对稳定，符合实际。表9 中95%置信区间即是相应方案的编码水平，实际水平是对应的实际水肥用量，具体为：将灌水量、有机肥及氮、磷、钾肥用量依次控制为488.3～508.7 mm、19.3～21.8 t/hm2、498.4～565.6 kg/hm2、399.7～447.1 kg/hm2、698.1～777.9 kg/hm2，可望获得较高的番茄产量，同时兼具较高的品质。

表9 番茄产量-品质评价值在-250～-150的450个方案中各因素水平的频率分布Table 9 Frequency distribution estimated value of tomato yield and quality varying from -250 to -150 among 450 scenarios for each factor level

3 讨 论

构建番茄产量-品质综合评价模型、分析其对水肥供应的响应，可为通过调控水肥管理提高番茄产量与品质提供理论依据，达到合理利用水肥资源的同时，提高农业生产水平。本文采用隶属函数分析法、主成分分析法、灰色关联度分析法和基于组合赋权的TOPSIS 模型4 种单一方法对不同水肥用量番茄的产量-品质进行综合评价，32 个处理中9 个处理的评价值排名相差较小，标准差在1.0及以下（表3）。原因可能在于单一评价方法各自从不同角度出发，对评价对象的信息利用和挖掘深度不同所致[2,6,8,17]。这4 种单一评价方法中，隶属函数法的结果与其他3 种的综合相关性最强（表4），而且计算简便，需要快速得到评价结果时，推荐使用隶属函数分析法。尽管本文将基于组合赋权的TOPSIS 模型作为一种单一评价方法参与后续的组合，该方法在运算过程中其实是综合了主客观两方面权重，也有组合评价的思想，实质是一种比较简单的组合评价方法。

本研究发现，供试的4 种组合评价方法中，Borda 与Copeland 组合评价方法原理简单且计算最为简便，但评价结果较差（表6），可能与组合过程只提取了单一评价方法结果的序值信息[26-27]有关，因而不推荐使用。模糊Borda 组合评价法得到的评价结果优势最为明显，很大程度上是由于该组合过程提取了单一评价方法结果的评价值和序值两方面信息，且计算简便[28]；基于整体差异组合评价方法与模糊Borda 法的结果相近，原因可能在于该方法的组合过程提取了单一评价方法结果的评价值信息，而评价值所包含的信息远大于序值[21]，计算的复杂程度与模糊Borda 组合评价法也相当。因而，这后两种组合评价方法可推荐使用。

本研究采用模糊Broda 组合评价模型将番茄产量和6个单一营养品质指标转化为能反映番茄产量-品质总体特征信息的综合指标，克服了多种评价方法结论不一致的问题，也可达到舍短取长的效果，结果可用于番茄水肥管理决策。基于模糊Broda组合评价模型的番茄产量-品质综合评价指标与水肥用量间的回归模型表明，当其他因子为中水平时，番茄产量-品质评价值随灌水量、施氮量、施磷量或有机肥用量的增加均呈凸形抛物线型变化。氮肥和灌水量对番茄产量-品质评价值的影响较大，其次是有机肥，磷肥的效应较小。这与单一品质指标或产量对水肥用量的响应研究基本一致[29-32]。有研究表明，氮肥、有机肥和灌水量对番茄果实可溶性固形物的影响较大[31]，施氮量对番茄红素含量影响最大[32]。在一定范围内，随着施氮量增加，番茄产量迅速上升，当超出限度后，产量下降[33]。但是也有研究表明，磷肥对番茄营养品质的影响最大，氮肥次之[14]，这可能与不同试验所控制的施肥量、采用的供试土壤、作物品种及栽培方式等不同有关。本研究发现，在对番茄产量-品质综合评价值的影响方面，灌水量和有机肥用量间具有拮抗作用，氮、磷肥用量间存在协同作用，表明灌水量增大时会减小有机肥对番茄产量品质的提升作用，施氮量增大会促进磷肥对番茄产量品质的提升作用。因而，要获得较高的番茄产量及品质，水肥用量要控制在合适范围。

选择恰当的评价指标、建立正确的评价模型对番茄水肥管理进行综合评价，目前仍是一个值得深入研究的问题。要使评价结果更加准确地反应实际情况，需要不断完善评价指标体系和评价模型。目前，有学者在探讨将单一方法组合的适用性和相容性[34]。也有学者在组合评价结论的基础上进行二次组合[35]，这在克服某些不足的同时，也增加了计算过程的复杂性。本文采用组合评价模型得出的结论有待实践的进一步检验。

4 结论

1）依据隶属函数分析法、主成分分析法、灰色关联度分析法和基于组合赋权的TOPSIS 模型4 种单一的综合评价法，32 个试验处理的评价值排名存在明显不一致，但各单一评价模型的评价结果与其他3 种的Kendall 相关系数通过了Kendall-W 协和系数事前检验，具有相容性，可进行组合评价。

2）Borda 评价法、Copeland 评价法、模糊Borda 评价法和基于整体差异的组合评价法与各单一评价模型评价值的Spearman 相关系数均在0.866 以上，反映了组合评价模型的合理性。其中，模糊Borda 组合评价模型的等级相关系数表现最优。

3）各水肥因素对番茄产量-品质模糊Borda 组合评价模型评价值的影响效应为：施氮量（函数变幅值Si=155.90）≥灌水量（Si=154.36）＞有机肥用量（Si=133.79）＞施磷量（Si=92.95）＞施钾量（Si=0）。其他因子为中间水平时，番茄产量-品质评价值与灌水量及氮、磷肥和有机肥用量的关系均呈开口向下的抛物线变化，不随施钾量变化。施氮量和施磷量的交互作用对提高番茄产量-品质有促进作用，灌水量和有机肥用量的交互作用则相反。

4）模型寻优表明，将灌水量、有机肥及氮、磷、钾肥用量依次控制为488.3～508.7 mm、19.3～21.8 t/hm2、498.4～565.6 kg/hm2、399.7～447.1 kg/hm2、698.1～777.9 kg/hm2，可望获得较高的番茄产量，同时兼具较高的品质。