飞机的垂直机动边界性能研究*

潘 军 陈柏松 华 欣

（空军航空大学 长春 130022）

1 引言

随着实战化训练的实施，常规训练已经不能满足现代空战的要求。飞包线，飞边界已经成为飞行训练的常态，这对飞行员掌握飞机的边界性能提出了较高的要求。同时，垂直机动动作是一类可以迅速占领优势高度和优势机头指向的机动动作，实战意义重大。为此，本文利用Matlab/Simulink仿真平台，以某型飞机为例，建立了垂直机动边界性能的计算模型，运用数值计算方法，分析了半斤斗滚转不同进入高度对应的最小进入速度、半滚倒转不同进入高度对应的最大进入高度和半滚倒转不同进入速度对应的地面安全高度三类边界性能指标，为开展飞行训练提供参考。

2 垂直机动模型的构建

2.1 垂直机动的方程

飞机在做垂直机动动作时，认为运动平面和竖直方向夹角为0，不考虑飞行中的侧滑，由此可得到飞机在垂直面内的运动方程［1］为

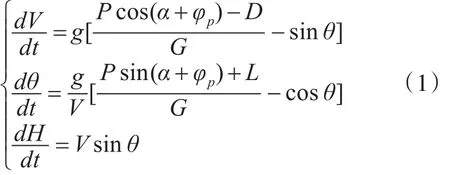
式（1）中，V表示飞机的飞行速度；P表示发动机的可用推力；g表示重力加速度；α表示飞机的飞行迎角；φP表示发动机安装角；D表示飞机所受的阻力；G表示飞机重力；L表示升力；θ表示轨迹角；H表示高度。

在垂直机动的过程中，通常都集中精力控制飞行过载来控制飞行轨迹，分析中取飞行过载为控制变量，由过载表达式［1］：

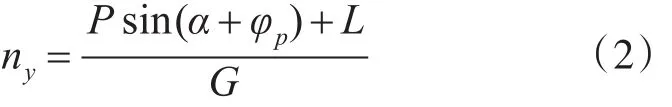
式（2）中，ny表示飞机的法向过载。

由此可以得到飞机垂直机动的计算模型为

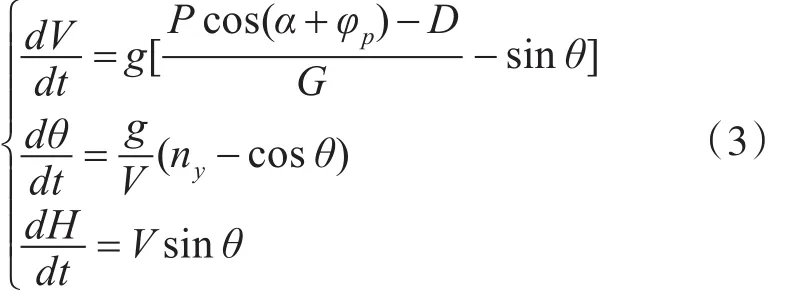
2.2 大气环境模型

1）标准海平面大气参数

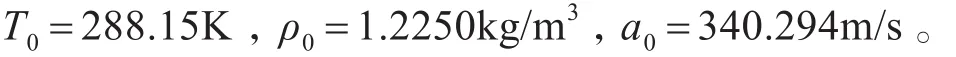
其中，T0表示标准状况下海平面处气温；ρ0表示标准状况下海平面处空气密度；a0表示标准状况下海平面处声速。

2）高度H下的声速、大气密度和温度

飞行高度H均在11000m以下，可以由如下计算公式［1］，换算不同高度下的声速、大气密度和温度。

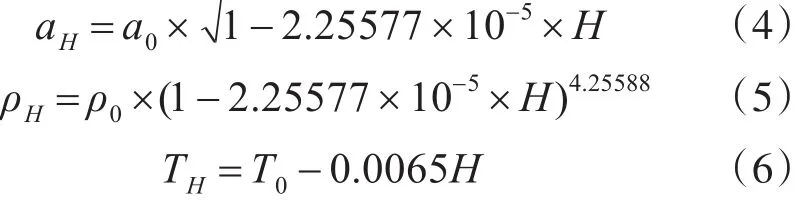
式（4）～（6）中，aH为 H 高度的声速，ρH为 H高度的空气密度，TH为H高度的温度。

2.3 升力系数和阻力系数模型

升力系数和阻力系数是随迎角、飞行马赫数变化的函数，结合飞行手册中的气动数据，对数据进行多项式插值，可以得到升力系数和阻力系数随迎角和飞行马赫数的变化关系式：

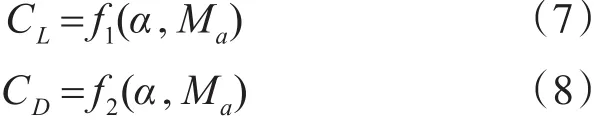
式（7）～（8）中，Ma表示飞行马赫数；CL表示升力系数；CD表示阻力系数；f1表示升力系数的插值函数；f2表示阻力系数的插值函数。

2.4 可用推力模型

发动机的可用推力主要受到飞行马赫数、飞行高度、温度这三类外界因素的影响。因此，根据手册中提供的的发动机可用推力随这三类因素变化的数据进行多项式插值，可以得到到相关状态下推力的表达式：

式（9）中，f3表示发动机可用推力插值函数。

3 垂直机动数值计算方法

3.1 计算步骤

半斤斗滚转的上升段是一个以动能换取势能的过程，由于飞行速度不断地减小，为了保持过载，迎角需要不断增大。但是，迎角又不能无限增大，因为迎角过大有可能使飞机失速，所以，当根据过载反推出的半斤斗滚转上升段某一点迎角大于该点的抖动迎角时，只能以抖动迎角进行飞行。

飞行员以某一过载拉起，随着高度上升，速度下降，为了保持规定过载，要不断拉杆增大迎角，当实际使用迎角大于抖动迎角时，则按照抖动迎角飞行。

当α＜α抖动：

式（10）中，f4为过载值的插值函数。

当α＞α抖动：

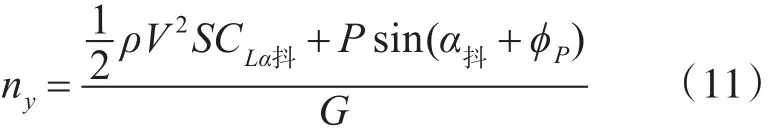
在式（11）中，CLα抖为抖动迎角 α抖对应的升力系数。

半滚倒转的下降段中，如果出现根据过载反推出的迎角大于抖动迎角的情况，最大迎角也只能使用抖动迎角飞行，迎角计算方式如式（10）～（11）。

相应的计算步骤如下。

1）给定初始条件：

海平面温度T=T0，各点处g=g0，斤斗运动进入的速度V0，高度H0。

2）数值计算：

（1）采用Matlab自带的定步长龙格库塔法ode4对式（3）进行数值积分，步长为0.01s。

（2）根据飞行高度H计算出该高度下的声速aH，再计算出对应的马赫数Ma=V/aH。

（3）根据式（9）计算出推力P的大小。

（4）根据马赫数Ma查到与之相对应的抖动迎角α抖动，根据式（10）和（11）求出对应的过载值。

（5）根据阻力系数的计算式（8），求出对应的阻力D。

以上的步骤同时进行，就可以完成完整的数值积分过程。

3.2 垂直机动计算结果验证

计算条件：某型飞机以干净构型进行半斤斗滚转动作飞行，对半斤斗滚转的上升段进行研究。上升过程中发动机处于最大工作状态，飞行质量7300kg，按照手册中给出的关键点过载设置对应载荷，其余位置载荷使用按线性均匀变化得到。

给定计算条件后，使用本文建立的飞机垂直机动模型进行计算，计算结果和手册数据的对比结果如表1。

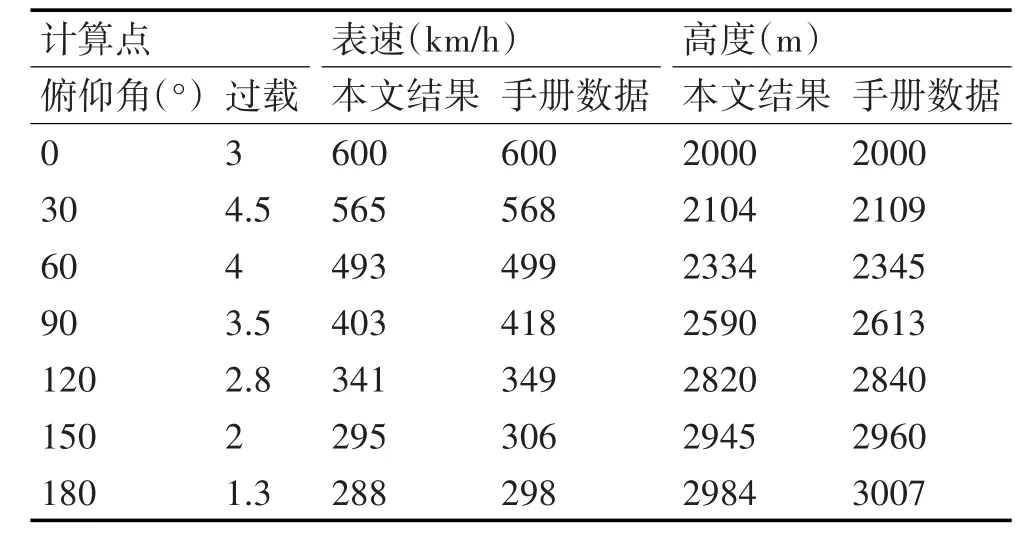
表1 计算数据和手册数据对比

根据表1知，给定相同的初始条件过载控制规律，本文模型计算出的结果略有偏差，分析其原因主要有三个方面：

1）本文的计算模型将飞机运动过程中飞行质量视为常数，但是飞行中由于燃油的消耗，质量一直在减小，这就出现一定的质量误差。

2）半斤斗滚转上升段中，由于计算得到的速度和手册的速度存在差异，所以实际使用的迎角并不不完全相同，这也是造成高度误差的原因之一。

3）本文给定的过载控制规律是根据几个关键点确定的，线性均匀变化的结果会与实际情况存在偏差，同时由于不同发动机的推力也存在误差，所以计算结果和手册数据不可能完全相同。

但是，本文的计算结果和手册数据比较接近，误差较小，所以可以使用本文构建的计算模型对某型飞机的垂直机动进行研究。

4 垂直机动边界性能

为了更好地分析垂直机动的边界性能，这里对垂直机动中的半斤斗滚转和半滚倒转两类运动进行研究。半斤斗滚转上升段中，发动机以最大状态工作，飞机按给定的过载规律控制，飞机沿轨迹上升。半滚倒转下降段中，发动机工作在相应的典型工作状态，飞机也按给定的典型轨迹角下的过载进行取值。

4.1 半斤斗滚转边界性能

半斤斗滚转的上升段是完成完整运动的基础，如果飞机无法满足半斤斗滚转的顶点速度要求，必然无法完成完整的半斤斗滚转运动。

飞机沿着半斤斗滚转上升段轨迹上升时，以速度换取高度，上升段是一个减速过程。飞机的速度不断地减小，但是又不能过小，否则由于舵面偏角限制，操纵性会下降，因此顶点速度必须保持在某一规定值之上。操纵规律一定的情况下，半斤斗滚转进入的高度和速度就要受到限制。所以，半斤斗滚转运动的边界性能可以用底边高度和最小进入速度的关系表示。

计算条件：为了满足飞机的机动性要求，半斤斗滚转顶点的飞行速度不能小于该型机最小操纵速度要求，可以计算出斤斗运动不同底边高度下进入速度的边界值。

在半斤斗滚转顶点最小操纵速度要求为表速不小于最小操纵表速V表min，表速的计算公式为

可以换算出对应的顶点真速应满足如下关系：

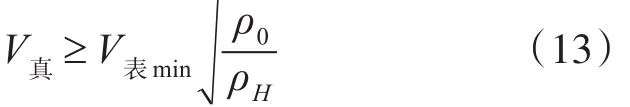
参考文献［2］，为了更加贴近某型飞机的使用特点，以如下关键点作为过载控制规律ny=f(θ)的插值节点，其余位置用线性插值得到，对半斤斗滚转边界性能进行研究。

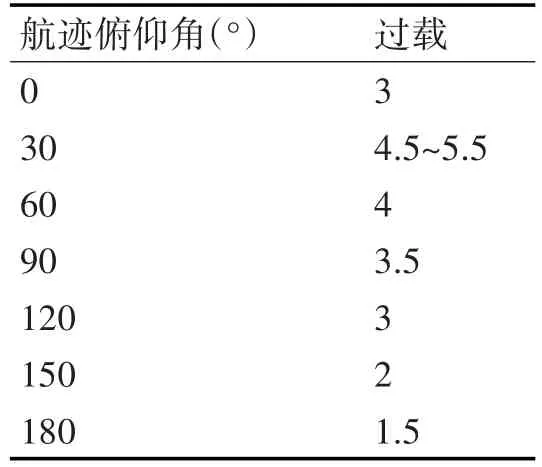
表2 半斤斗滚转上升段不同俯仰角处的过载值

半斤斗滚转上升段的速度损失和拉起过载有很大关系。如果半斤斗滚转刚开始拉起时的过载大，诱导阻力也大，能量损失多，相应顶点速度就会减小，所以拉起时的过载不能过大。但是半斤斗滚转上升段的过载又不能过小，过载小会造成曲线运动半径增大，完成半斤斗的运动增加，飞机上升高度多，重力势能增加多，这也会造成顶点的速度小。为了得到更符合飞行实际的半斤斗滚转边界性能，必须考虑不同的过载控制规律。

航迹角30°是一个特殊的角度，该点选择不同的过载会直接影响到半斤斗滚转上升段的轨迹。对于某型飞机，航迹俯仰角30°处的过载可以取4.5、5或5.5。这里对30°俯仰角处的每一个过载值都进行进行边界性能计算，求出不同高度下的最小进入速度，即可得到半斤斗滚转的边界性能。

在Matlab/Simulink仿真平台中搭建相应的计算框图进行仿真计算，结果如图1～2所示。

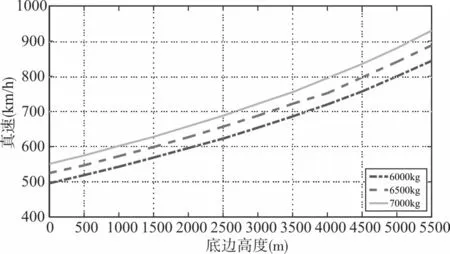
图1 不同底边高度的半斤斗滚转最小进入表速

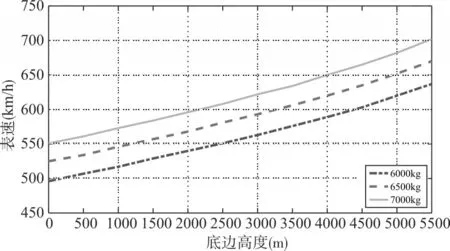
图2 不同底边高度的半斤斗滚转最小进入真速

从计算结果可以看出，以飞行质量6500kg为基准，斤斗底边进入高度每增加1000m，最小进入表速增加约25km/h；斤斗底边进入高度每增加1000m，最小进入真速增加约63km/h。飞行质量每增加100kg，相同底边高度上的进入表速增加约6km/h，进入真速增加约7km/h。

4.2 半滚倒转边界性能

半滚倒转的运动情况不仅受过载规律的影响，还会受到发动机使用的影响。在半滚倒转下降段中，发动机一般处于慢车状态或者额定状态，慢车状态下，飞机速度相对较小，旋转角速度大，完成机动动作的时间较短，高度损失相对也较小；如果使用额定状态，飞机速度大，虽然完成机动动作的时间较长，但是飞机能量损失小，对占据空战优势较为有利。为了更加贴近飞行实际，半滚倒转下降段中，不同位置的发动机工作状态如表3所示［2］。

表3 半滚倒转下降段发动机的工作状态

半滚倒转下降段中，飞机沿轨迹加速向下运动，必须保证改出时飞行速度不超过改出高度上的最大速度限制，如表4；同时，飞机在飞行过程中，也有一定的安全高度限制，确保不触地发生危险。斤斗下降段运动的边界性能可以用不同进入高度下的最大速度来表示。

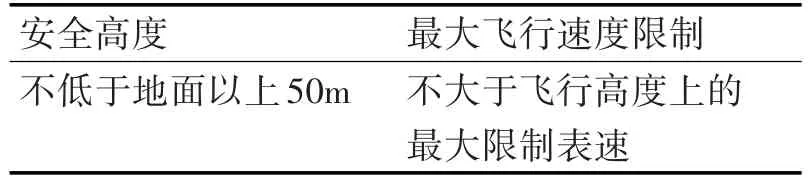
表4 安全高度和速度限制

计算条件：飞机在改出斤斗时，需要满足两个条件：一是改出速度小于该高度下的最大飞行速度限制，二是底边安全高度高于规定限制值。

参考文献［2～3］，飞机的典型轨迹角与过载的关系按照表5所示的关系取值，其余点处过载利用线性插值插值得到。

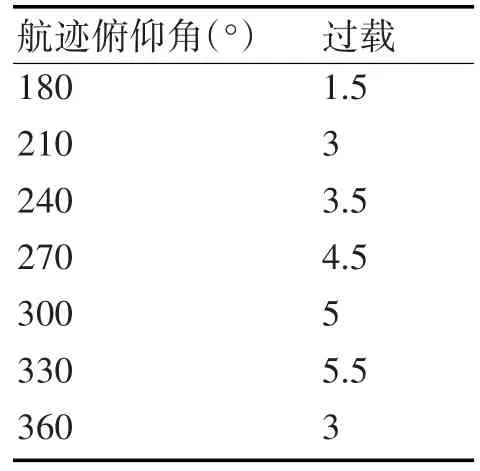
表5 半滚倒转下降段不同俯仰角处的过载值

在Matlab/Simulink仿真平台中搭建相应的计算框图进行仿真计算，结果如图3～图6所示。图3所示的是半滚倒转下降段使用慢车状态，不同高度下的半滚倒转最大进入表速曲线，图4是对应的真速曲线。图5所示的是半滚倒转下降段使用慢车状态，不同高度下的斤斗最大进入表速曲线，图6是对应的真速曲线。

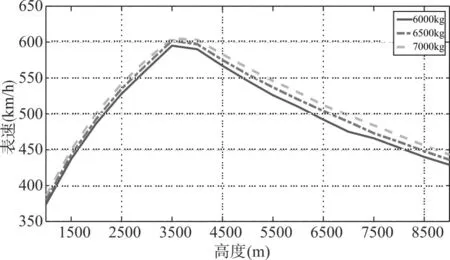
图3 半滚倒转最大进入表速（慢车）

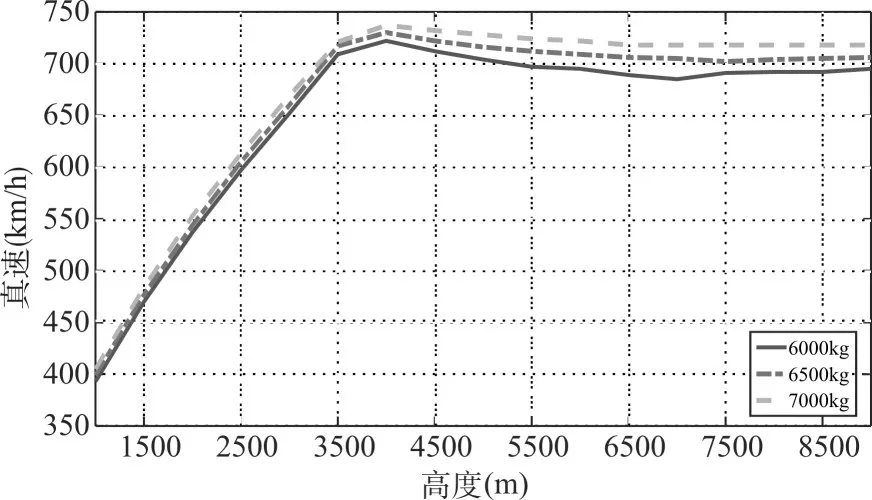
图4 半滚倒转最大进入真速（慢车）

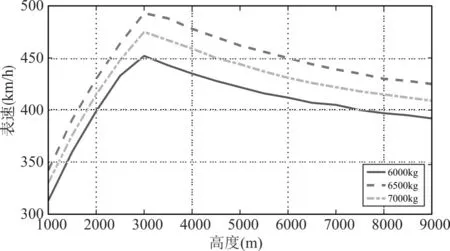
图5 半滚倒转最大进入表速（额定）

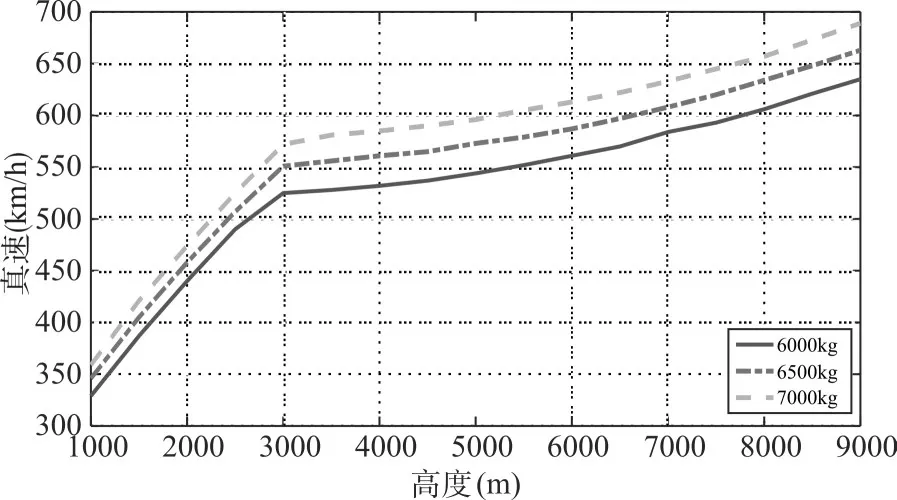
图6 半滚倒转斤斗最大进入真速（额定）

对于半滚倒转下降段使用慢车状态的情况，顶点高度3500m以下时，最大进入速度主要受到安全高度限制，高度每增加1000m，最大进入表速增加约125km/h，真速增加约130km/h，最大进入速度与质量关系不大。顶点高度3500m以上时，最大进入速度主要受到最大飞行马赫数限制。顶点高度3500m以上时，高度每增加1000m，最大进入表速减小约32km/h，最大进入真速基本不发生变化；飞行质量每增加100kg，最大进入表速增加约2km/h；最大进入真速增加约3km/h。

对于半滚倒转下降段使用额定状态的情况，顶点高度3000m以下时，最大进入速度主要受到安全高度限制，以6500kg为基准，高度每增加1000m，最大进入表速增加约73km/h，真速增加约103km/h；质量每增加100kg，最大进入表速增加约4km/h，真速增加约5km/h。顶点高度3000m以上时，最大进入速度要受到最大飞行马赫数限值，以6500kg为基准，高度每增加1000m，最大进入表速减小约11km/h，最大进入真速增加约19km/h；飞行质量每增加100kg，最大进入表速增加约20km/h；最大进入真速增加约25km/h。

5 地面高度变化的垂直机动边界性能

地面安全高度指的是为了保证斤斗下降段运动过程中，为了保证飞机在向下运动的过程中不发生触地的危险，地面与飞机的高度差始终大于50m的地面最高海拔高度。如果在高原地区进行垂直机动飞行训练，由于地面高度增加，在半滚倒转下降段中，为避免触地危险，最大进入速度也会发生变化。实际飞行中，要根据不同速度的掉高度情况，分析垂直机动边界性能，合理选择进入高度速度，保证飞行安全。

计算条件：标准大气条件下，飞行质量为6500kg，轨迹角190°～330°之间时，发动机使用慢车工作状态，其余位置如表3，过载控制规律如表5。进入速度在最小操纵速度和对应顶点高度上的最大进入速度之间变化，分析半滚倒转不同进入速度下的地面安全高度。

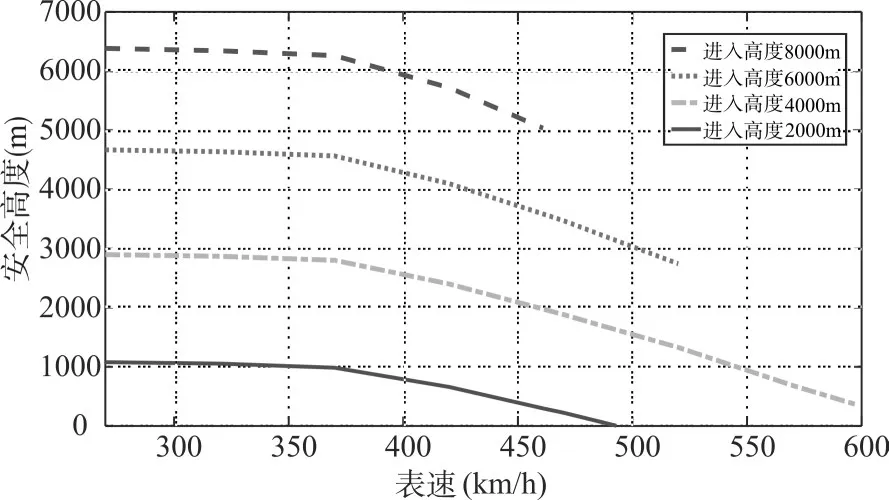
图7 不同进入表速对应的地面安全高度

从计算结果可以分析得到，地面安全高度受进入高度和进入速度两个因素共同影响。进入表速小于370km/h时，各进入高度的地面安全高度基本不受速度影响；进入表速大于370km/h时，在小于最大进入表速的情况下，相同高度下，速度每增加50km/h，地面安全高度要降低约450m。

6 结语

本文通过构建飞机的垂直机动的计算模型，给出了垂直机动的数值计算方法，以某型飞机为例，对垂直机动不同底边高度的最小进入速度和不同顶边高度的最大进入速度进行了分析，分析了不同进入表速对应的地面安全高度。计算结果表明，底边高度增加，半斤斗滚转最小进入速度也要相应增加；顶边高度增加，半滚倒转最大进入速度同样会增加；随着地面高度增高，需要减小半滚倒转的进入速度以保证飞行安全。本文所给出的是一种通用计算模型，可以推广到不同机型的和不同构型的垂直机动边界性能的计算中，实用性较强。在飞行过程中，飞行员需要根据飞行条件，结合理论分析结果进行飞行准备，力求将飞行训练的效果达到最大化。