数学问题解答
2019年9月号问题解答
(解答由问题提供人给出)
2501设△ABC的三内角A,B,C所对的三边长分别为a,b,c,三角形的面积△,求证:
(1)
当且仅当△ABC为等边三角形时式中等号成立.
(河南质量工程职业学院 李永利 467000)
证明令a=y+z,b=z+x,c=x+y,

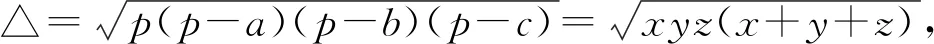
而 2(ab+bc+ca)-(a2+b2+c2)
=2[(y+z)(z+x)+(z+x)(x+y)+(x+y)(y+z)]-[(y+z)2+(z+x)2+(x+y)2]
=2[(x2+y2+z2)+3(xy+yz+zx)]
-[2(x2+y2+z2)+2(xy+yz+zx)]
=4(xy+yz+zx),
于是(1)式等价于
⟺(xy+yz+zx)2≥3xyz(x+y+z)
⟺(xy)2+(yz)2+(zx)2+2xyz(x+y+z)≥3xyz(x+y+z)
⟺(xy)2+(yz)2+(zx)2≥xyz(x+y+z)
(2)
而(xy)2+(yz)2+(zx)2≥xy·yz+yz·zx+zx
·xy=xyz(x+y+z),
即(2)式成立,从而(1)式成立.
由以上证明过程可知,当且仅当x=y=z即a=b=c亦即△ABC为等边三角形时,(1)式中等号成立.
2502设AM为锐角三角形ABC的外接圆直径,N为边BC的中点,P为∠BAC的平分线AP与直线MN的交点,E,F分别为点P在两边AB和AC上的射影,证明:直线MN与EF的交点H是△ABC的垂心.
(河南辉县一中 贺基军 453600)


证明如图,在△ABC及其外接圆中,因∠BAC的平分线AP与所给直线MN相交,
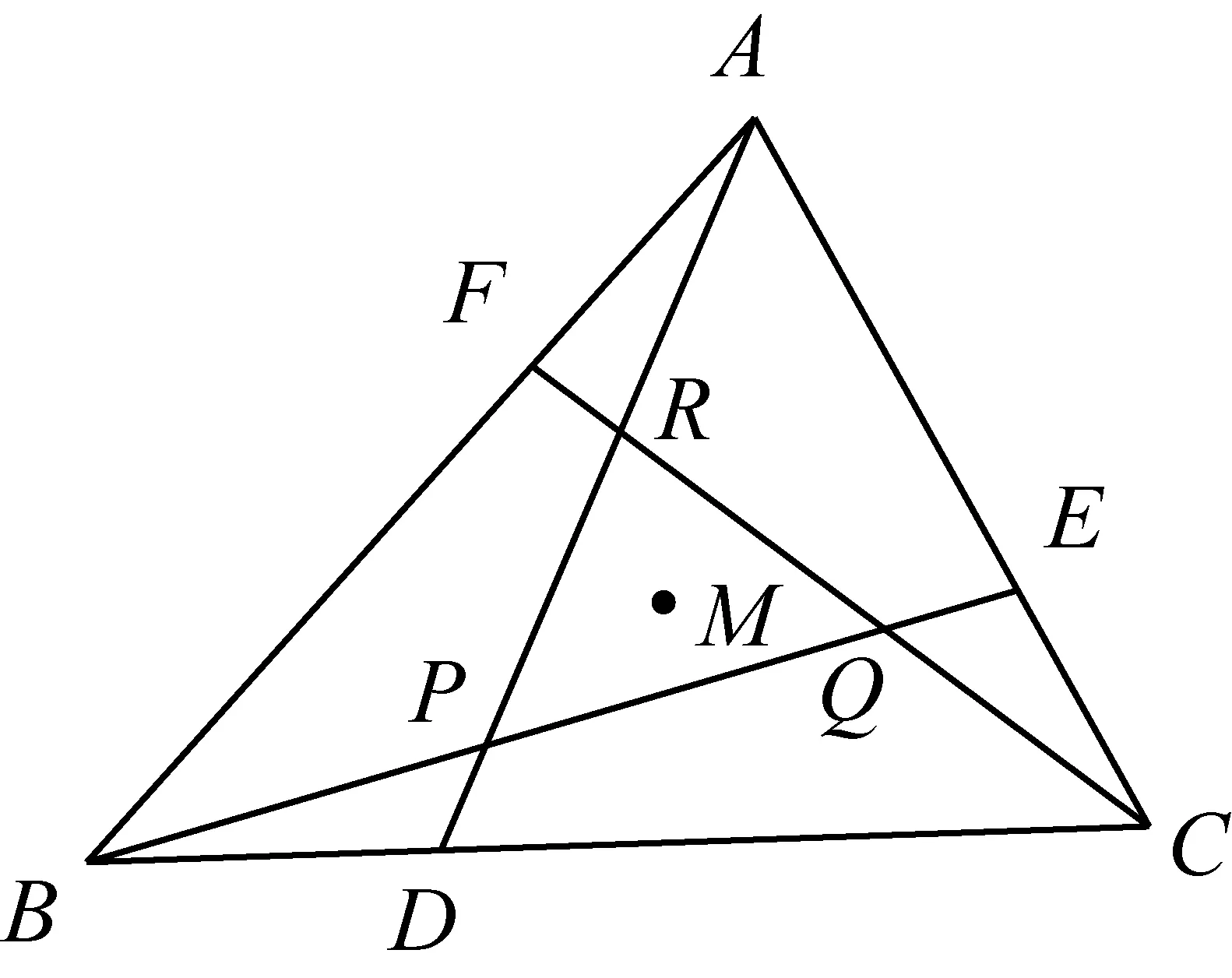
故知AB≠AC,不妨设AB 设直线MN与△ABC外接圆的另一交点为Q, 连接QA,QB,QC,QE,QF及MB,MC. 因AM为△ABC外接圆的直径, 故∠AQP= 90°. 又因∠AEP=∠AFP= 90°, 故A,Q,E,P,F五点共圆. 因∠QEA=∠QFA, 故∠QEB=∠QFC. 又因∠QBA=∠QCA, 故△QBE∽ △QCF, ① 在四边形QBMC中, 由BN=CN得S△QBM=S△QCM, 即BQ·BM·sin∠QBM =CQ·CM·sin∠QCM. 因∠QBM+∠QCM=180°, 故BQ·BM=CQ·CM. ② 在线段NQ上截取NH′ =MN, 连接H′E,H′F及H′B,H′C, 所得四边形H′BMC为平行四边形(因该四边形对角线互相平分). 因BH′∥MC,MC⊥AC, 故BH′⊥AC,同理CH′⊥AB. 因此,点H′ 是△ABC的垂心, 同时∠EBH′ = 90°-∠BAC=∠FCH′. 根据① ②及CM=BH′,BM=CH′ 得 由此可知△EBH′ ∽ △FCH′, 从而有∠H′EB=∠H′FC. ③ 由题设知AE=AF,∠AEF=∠AFE, 从而有∠HEB=∠HFC(③式的特例). ④ △ABC的垂心H′ 和点H在线段NQ上, 考虑线段NH′ 与NH的关系: 如果NH′ =NH,此时点H′ 重合于点H; 如果NH′ >NH,结合③ ④得 ∠H′EH=∠H′EB-∠HEB =∠H′FC-∠HFC=∠H′FH, 于是△EH′F为等腰三角形, 其顶点H′ 在边EF的中垂线AP上, 即△ABC的垂心H′ 在AP上, 因此AP⊥BC. 又因AP平分∠BAC, 故AB=AC,这与AB≠AC矛盾; 同理,NH′ 综上得知,H′ 和H两点重合, 因此点H是△ABC的垂心. 2503△ABC中,a,b,c分别表示三角形三边长,I为△ABC的内心,则 (浙江省永康市第六中学 吕永军 321300) 证明设r,R分别为△ABC的内切圆半径与外接圆半径 2504已知a,b,c>0,abc=1,求证: (河南省南阳师范学院软件学院 李居之 孙文雪 473061) 证明不难证明,当x>0时, xlnx≥x-1(当且仅当x=1时等号成立), 所以,当x>0时,有 于是 当且仅当a=b=c=1时等号成立. 2505如图,△ABC中,D,E,F分别是边BC,CA,AB上的点,且,BD=mBC,CE=mCA,AF=mAB,0 (湖北省公安县第一中学杨先义434300) 证明设M是△ABC的重心. 熟知下述引理: 所以△ABC与△PQR的重心重合. (来稿请注明出处——编者) 2506在k边形A1A2…AK(k≥3)中,a1,a2,…,ak为其各边长,s为周长,n∈N+且n≥2,0<λ≤1,求证: (安徽省岳西中学 储百六 246600) 2507如图,已知四边形ABCD,E、F、I、J分别是四边的中点,分别连接AJ、IB、DJ、IC交G、H,IJ、EF交O,求证:GH∥EF. (江西师范高等专科学校 王建荣 335000) 2508在锐角△ABC中,有 (天津水运高级技工学校 黄兆麟300456) 2509如图,在△ABC中,∠BCA的平分线与△ABC的外接圆交于点R,∠BCX=∠ACY,边BC的垂直平分线交CX于点P,边CA的垂直平分线交CY于点Q,K是BC的中点,L是AC的中点,则△RPK和△RQL面积相等. (安徽省旌德中学 赵忠华 242600) 2510已知a,b,c>1,a+b+c+2≥abc,求证: (陕西省咸阳师范学院教育科学学院 安振平 712000)

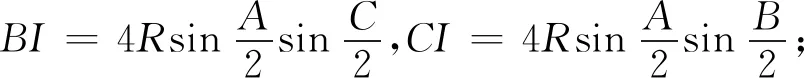


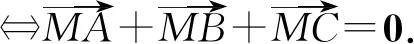
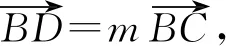
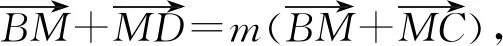


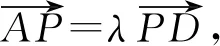



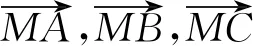



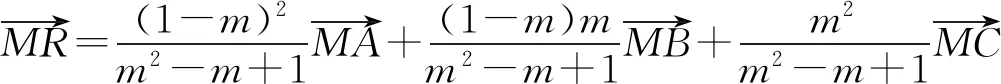
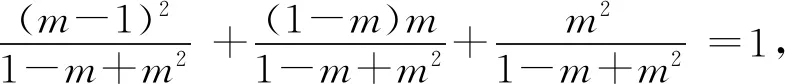

2019年10月号问题



