解析几何问题中的“设点法”求解策略

张明建

(福建省浦城县第一中学 353400)

由于圆锥曲线的最值、定值、定点问题是近年高考的高频考点，对考生分析、解决问题的能力要求较高，具有一定的难度和区分度，所以本文拟通过归类解析的形式，着重帮助学生理清如何借助“设点法”巧妙处理此类问题.

一、处理圆锥曲线中的最值问题

在圆锥曲线与直线、圆、向量等知识的综合问题中，求解有关最值问题时，往往需要灵活运用“设点法”，先获得与目标问题紧密相关的一个代数式，再结合基本不等式求解最值.

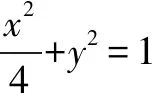
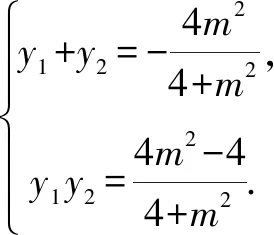
设直线l与椭圆长轴交于点M，则可得M(2m,0)，又由图易知y1y2<0，

所以S△OPQ=S△OMP+S△OMQ

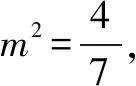
二、处理圆锥曲线中的定值问题

在圆锥曲线与直线、圆、向量等知识的综合问题中，求解有关定值问题时，往往需要灵活运用“设点法”，关键在于结合目标问题进行相关的字母形式的代数运算，并获得化简结果为定值.

解析因为抛物线y2=2px(p>0)的焦点坐标为(1，0)，则抛物线的标准方程是y2=4x.由题意知直线l的斜率存在，设直线l的方程为y=kx+2(k=0)，

得k2x2+(4k-4)x+4=0.

设点A(x1,y1)，B(x2,y2)，则

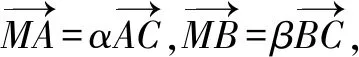
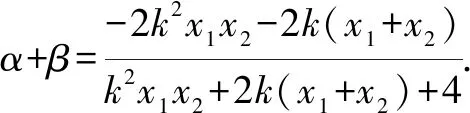
将(*)代入化简得

α+β=-1.

故α+β为定值，且定值为-1．

评注本题求解的关键是灵活运用“设点法”，先求出关于直线l与抛物线的二元一次方程，然后将二者交点A，B两点设出，之后根据二元一次方程的性质构建根与系数之间的关系，从而求出答案.本题侧重通过进行一些相关的代数运算，达到证明或探究的目的，突出地体现了高考考查的一个很重要的核心素养——数学运算.

三、处理圆锥曲线中的定点问题

在圆锥曲线与直线、圆、向量等知识的综合问题中，求解有关定点问题时，往往需要灵活运用“设点法”，对于证明直线恒过定点问题，需要灵活运用直线方程的点斜式或斜截式加以分析；对于考查是否存在定点问题，需要灵活运用先假设存在，再合情推理的思路加以分析.

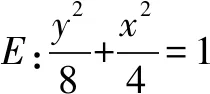
解析假设存在定点N(x0,0)满足题设条件.

当PQ⊥x轴时，由椭圆的对称性可知恒有∠PNM=∠QNM，即x0∈R.

当PQ与x轴不垂直时，设PQ的方程为y=k(x-1)，代入椭圆方程化简得：

(k2+2)x2-2k2x+k2-8=0.

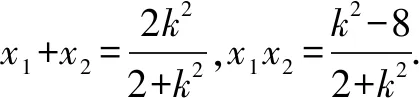
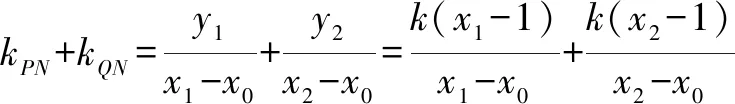
(x1-1)(x2-x0)+(x2-1)(x1-x0)

=2x1x2-(1+x0)(x1+x2)+2x0

又由∠PNM=∠QNM，得kPN+kQN=0,

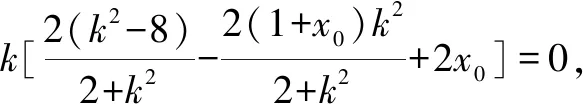
整理得k(x0-4)=0.

又注意到k∈R,所以x0=4.

综上，在x轴上存在定点N(4,0)，使得∠PNM=∠QNM.

评注本题第二问求解的关键在于以下两点：一是必须明确“是否存在型”问题的常用处理方法，即考虑题设的所有条件，并进行正确的分类讨论，将各种情况逐一进行解答；二是运用设点法的一般原则，将椭圆与动直线相交的问题转化为一元二次方程，然后设点，再结合一般情况下∠PNM=∠QNM可等价转化为kPN+kQN=0，从而便于与具体的代数运算紧密起来，有效地解决问题.

总之，处理圆锥曲线中的有关“最值、定值、定点”问题时，往往需要灵活运用“设点法”以及相关数学思想方法. 此外，结合上述归类解析，希望能够帮助学生进一步提高分析、解决问题的能力以及对所学数学知识、方法的综合运用能力.