巧画“示意图”，提高学生解决问题能力

陈乐乐

[摘 要]“示意图”在解决数学问题中起到“桥梁”作用，能实现从纯文字解决问题到算式解决问题的过渡，通过“纯文字解决问题→示意图解决问题→算式解决问题”，让学生清晰地知道解决问题中各个数的意义以及数量关系，直至整体把握题意，构建数学模型。掌握了应用“示意图”解决问题的策略，不仅能提高解决问题能力，还能发展数学思维。

[关键词]示意图;解决问题;能力

[中图分类号] G623.5[文獻标识码] A[文章编号] 1007-9068（2019）29-0023-02

解决问题是综合性、创造性地应用所学知识与方法解决新问题的过程，是小学数学的重点和难点。为了更好地把握学生解决问题的困难所在，我对四年级学生进行了问卷调查，实行全面把脉。通过问卷调查及实际了解分析，我发现学生解决问题的困难主要体现在：1.对题意理解不深刻，题目阅读不全面;2.不会分析数量关系，对于题目中各个数的意义无法有效把握，不能进行数与数之间的整合和梳理;3.混淆加减乘除的关系，看到题目中的几个字和数，就想当然地进行加减乘除运算，从而导致错误;4.解题方法策略单一，很难多角度思考、解决问题;5.能轻松完成图示问题或者图文结合问题，而对于纯文字的问题，解决起来比较吃力。

由此可看出，图文解决问题一般难度低于纯文字解决问题，为此，何不将纯文字解决问题转换为简单示意图，最后列式解决，即“纯文字解决问题→示意图解决问题→算式解决问题”。

一、画示意图在解决问题中的意义

学生在画示意图的过程中，会舍弃与数学问题无关的东西，抽取有用的数量关系，再把抽象的数量关系转化为具体形象的图示，体现了“数学思考”;整个解题过程循序渐进，将解决问题由“文字表征”向“图形表征”再向“数学表征”转化，对学生有效解决问题意义深远。

（一）画示意图便于提取有用信息，理解数量意义

【例1】18位小朋友参加乒乓球训练，每3人发2个乒乓球，一共需要发多少个乒乓球？

【分析】学生对“每3人发2个乒乓球”理解困难，不清楚题目中“3”和“2”的意思及关系，导致出现“3×2=6（个）”这样的错误。

【图解】

通过简单的示意图，重点抓住“每3人发2个乒乓球”，非常清楚地表达了18、3、2的意思，有效沟通了这三个数之间的关系。有了这些基础，列式也就水到渠成。

（二）画示意图便于把握整体过程，厘清数量关系

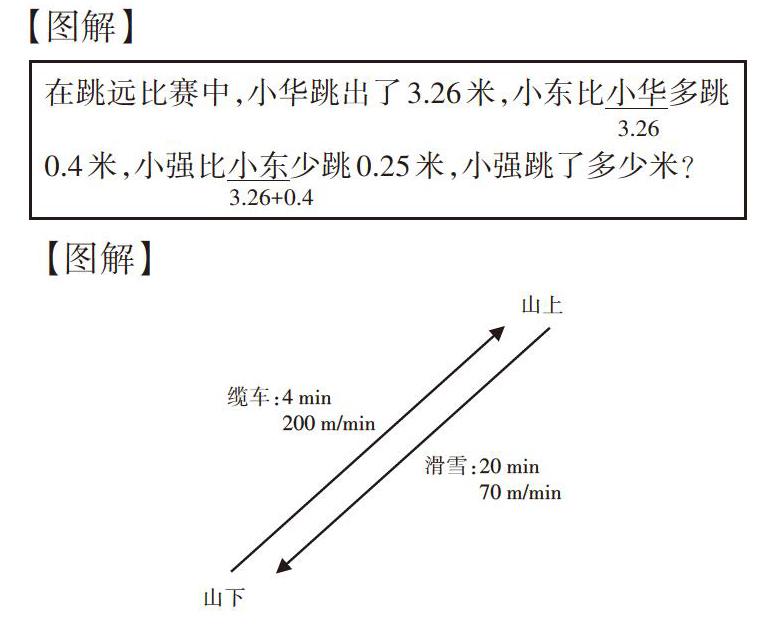
【例2】在跳远比赛中，小华跳出了3.26米，小东比小华多跳0.4米，小强比小东少跳0.25米，小强跳了多少米？

【分析】这类题涉及“比较”，人物多，关系也复杂，学生在练习中很容易搞不清状况。

只要将人物用相应的数代替，复杂的信息就清晰地展示在学生的面前。事实证明，学生不仅分清了数量，还能用自己的语言将解题的过程清晰地表达出来 。虽然只是小小地添个数，却体现了数学中重要的转换思想。

（三）画示意图便于构建数学模型，显现抽象过程

【例3】爸爸带明明去滑雪，乘缆车上山用了4分钟，缆车每分钟行200米，滑雪下山用了20分钟，每分钟行70米，他们滑雪行了多少米？滑雪比乘缆车多行多少米？

本题涉及的数比较多，问题也多，但有一个关键，就是这类题目带有故事叙述的味道，可以将问题过程用动态的示意图表示。图与文是相互的，看文字想到图，看图也可以想到文字，把问题转化为图示帮助构建模型来解决问题，构建模型的过程就是展示数学思维的过程。

二、促进学生画示意图解决问题的有效策略

（一）激发学生画示意图的内需，让学生体会画图的优势

策略不是可以教会的，而是体会之后的一种意识。从调查中我们发现，学生恰恰缺乏画示意图的意识，所以教师需要创设情境，让学生产生画示意图的内需。笔者尝试通过分组实验促进学生这种需求的生发。

情境问题：联华超市去年平均每月营业额9000元，今年预计能提前2个月达到去年的营业额，今年预计平均每月的营业额是多少？

对于此题，笔者将全班学生分成了两组，即实验组和对照组。

实验组（12人）：画图解决，全对的有10人，准确率83.33%，图示非常精彩。

 对照组（13人）：不画图，全对的有4人，准确率30.76%，多为对题意理解不到位导致的错误。错误展示如下：

让解题错误的学生利用画图进行二次解答，其解题的准确率大大提高。通过对比，二次解答，学生深刻体会到了画图的优势所在。

（二）从低段抓画图，循序渐进，增强画图意识

低段数学学习涉及的解决问题，基本以动态故事类或者静态故事类为主，由于学生有丰富的想象力，将此类问题转化为画图并不难。中段数学教学中，教师找一些可以画示意图的载体帮助学生规范画示意图，这样到了高段，就可实现学生一看到问题就会在脑中形成示意图，并据图进行解题，真正提高了学生解决问题的能力。因此，教师在教学解决问题时，应多让学生尝试用画示意图的方式解决问题，有效培养学生的画图意识。

1.模仿画示意图

在画图初期，学生会无从下手，教师可示范画图，学生则点评并模拟画图，也可以优生带动学困生，普及画图方法。平时多展示学生优秀的画图作品，将画图作品在班级里进行传阅。

在学生根据文字题画示意图并解答时，不要让他们解答完就了事，要让他们反过来再根据示意图说一说题意。遇见带图的问题，不要就题论题，要多让学生说一说图示传达的意思，哪些地方传递了关键信息，找到纯文字解决问题中的关键词与示意图中关键点的对应关系。

2.尝试自主画示意图

（1）画示意图前应进行文本解读，标注重要信息。学生在阅读问题文本时，可以对题目中的重要信息进行标注，例如画一画、圈一圈、写一写，这样会更有针对性地理解题意，表达数学思维。如：

本题的关键点是“照这样的速度”，据此画示意图，并重点理解，这道题也就迎刃而解了。

又如，在理解例题“果园里有苹果树625棵，比桃树多35棵。桃树有多少棵？”文本的过程中，如果这样标注：

解题就已经成功了一半，也就不会犯“见多就加，见少就减”的低级错误，同时也进一步强化了数学模型的正确运用——求大数用加法，求差和小数用减法，渗透了数学建模思想。

（2）培养学生的符号意识，掌握一定的画图技巧。要让学生利用各种简单的符号画示意图。小学阶段，学生接触过很多熟悉的数学图形及数学符号，常见的有：

可以赋予这些图形及符号各种意义，如圆、长方形等几何图形表示实物或总数，问号表示未知量，箭头表示去向，阴影表示已知的，线段表示部分，虚线或者斜线表示去掉，等等。有了这些素材，学生画示意图就有章可循了。

3.巩固画示意图

（1）强化画图意识。课前、课中、课后实时实地地进行画图。当学生解题有困难时，不要直接解释题意和提示算法，而是要引导他们通过画示意图整理信息，理解题意、形成思路、寻找解法，让他们在潜移默化中感受画图的妙处，将“画示意图”内化为自身的需求。

（2）示意图与其他方式并存。肢体语言、实物演示等与示意图有异曲同工之效，用肢体语言可表示解决问题的意思，帮助学生理解题意及数量的意义。在遇到难以理解的解决问题时，可以让学生边说题意，边做相应的肢体动作，深刻理解题意，为画图奠定基础，这是画图的一种雏形。如问题“小平和小红同时从A地到B地，小平每分钟比小红多走20米，30分钟后小平到B地立即沿原路返回，在离B地350米处遇到小红，小红每分钟走多少米？”，讓学生就题意现场模拟表演，并在探讨中不断改进，然后再用示意图将所模拟的情景画下来，这样数量关系就一清二楚了。

（三）将数学思想方法与“示意图”相融合

数形结合思想、对应思想、转化思想等是小学阶段常见的数学思想。在画示意图过程中，应及时渗透数学思想，直逼数学本质，让示意图与数学思想相辅相成。 如问题“4件上衣，3条裤子，一共有多少种不同的搭配方法？”，学生就会用不同的几何图案代表衣服和裤子，画出示意图。这个过程，关注的是几何图案和具体实物之间的一一对应关系，体现了数学中的对应思想。

有些问题按原题的条件、数量关系解答起来比较复杂，但换种方式思考，恰当地运用直观图形转化题中的数量关系，便会有一种豁然开朗的感觉，解决起来也特别轻松。如重叠问题，采用韦恩图就可以清楚地知道“共有”部分，从而顺利攻破难点，同时还能很好地渗透转换思想。

（责编 黄春香）