小学数学试卷命题改革“四策略”

陈敏

[摘 要]数学试卷是检测学生数学学习情况的有效载体。对传统的数学试卷的命题进行改革十分有必要，因为数学试卷要突显开放性、生活性、探索性、衔接性，培养学生的数学思维和创新能力，使学生体会数学的应用价值。

[关键词]数学试卷;命题;改革

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2019）29-0055-02

根据义务教育阶段课程改革的总体要求，教学要立足小学数学课程，通过让学生参与具体的数学学习活动，习得数学知识，掌握数学技能，这些课程改革的基本理念决定了小学数学试卷命题改革的方向。众所周知，数学试卷具有评价、指导和激励的功能，紧紧围绕课程改革的中心设计数学试卷，才是小学数学试卷命题改革的正确方向。

一、突显开放性，培养数学思维

1.条件的开放

为学生设计条件开放型题目，能够有效地培养学生的数学思维。

例如，（1）请根据算式（30-6）÷6编写一道应用题;（2）有54个苹果，拿出几个后，剩下的苹果是否可以平均分到8个盘子中？

2.解题策略的开放

解题策略开放型题目对于激活学生的思维是十分有益的。

例如，基于小数乘法这一知识点，可以设计开放题：根据答案中积的小数点的位置，在因数上点上小数点：（1）725×303 = 219.675;（2）218×13 = 0.283。

3.答案的开放

传统的应用题通常都只有唯一一个答案，学生的任务就是找出这个答案，而答案开放型题目则是根据选取的角度和思维的方式不同，会得到不同的答案。

例如， “六一”节期间，儿童公园为招揽游客，推出了优惠票价：购票满50张打八折;购票满40张打八五折;购票满30张打九折;30张以下的按原价收费，每张2元。假设某班师生共有45人，则一共有几种购票方案？请从中挑选出最佳购票方案。这样的题目既贴近学生的生活，又紧密结合教材内容，让学生能够运用所学知识予以解答，充分发挥了学生的学习能动性。

二、突显生活性，体会应用价值

根据新课程改革的理念，人人都要学有价值的数学，即要学习有用的数学。数学在人们的日常生活中应用十分广泛，大到航天器的设计，小到买米买菜，生活、生产、科学技术等方方面面都离不开数学，这也正是数学应用价值的体现。

1.基于生活素材编写试题

教师在编写试题时，应当根据学生的具体学情和生活经验，多从生活中寻找素材，让学生能够有的放矢地去解决实际问题，不断积累数学学习经验。

例如，秋游时，有52个同学去划船，有两种船，大船可以坐6人，小船可以坐4人，大船和小船每小时租金分别是8元和6元。（总计划船时间1小时）

（1）按照不留空位又不超载的总体要求，设计三种租船方案，并算出相应的租金。

方案一：假设全部同学都坐小船。52÷4=13（条），13×6=78（元）。需要13条小船，租金78元 。

方案二：假设全部同学优先坐大船。52÷6=8（条）……4（人），8×8+6=70（元）。 需要8条大船和1条小船，租金70元 。

方案三：如果既坐大船又坐小船，只能根据以上两种方案的结果进行排列组合，从大到小或者从小到大进行推算，再从中选取合适的方案。

2条大船和10条小船： 2×8+10×6=76（元） 。

4条大船和7条小船： 4×8+7×6=74（元）。

6条大船和4条小船 ：6×8+4×6=72（元）。

（2）请你找出最省钱的方案，并算出价钱。

学生通过列举和计算，就能从众多方案中找出最省钱的方案，即租8条大船和1条小船。在这个过程中，学生不仅需要列出完整的方案，还要根据具体的租船事宜，尽量考虑多租大船，但也要注意不留空余，只有满足这些条件才最省钱。

教师要善于挖掘生活中的素材，多设计一些富有挑战性的实际问题，把数学知识和学生的学习生活融会贯通，让学生在潜移默化中养成用数学思维认识和观察世界，用数学逻辑去分析和解决问题的习惯。

2.基于生活应用编写试题

教师命题时要谨记数学的应用价值导向，而不是仅仅关注具体的结论，要注重培养学生的数学思维和数学方法。

例如，有一台微波炉的体积约41立方分米，能不能装在一个长40厘米、宽35厘米、高30厘米的纸箱中？

这道题考查的知识点较多，学生在解决这类应用题时，不仅需要知道长方体的体积公式，算出微波炉包装箱的容积（40×35×30=42（立方分米） ），还要考虑到实际的包装，虽然纸箱的容积比微波炉大，但是还需要考虑微波炉的长、宽、高。这样的试题就能够有效地培养学生利用数学知识灵活解决实际问题的能力，以此促进他们数学核心素养的不断提升。

三、突显探索性，培养创新能力

前苏联著名教育实践家和教育理论家苏霍姆林斯基曾经指出，人的内心都有一种需要，希望能够成为一个发现者、研究者、探索者。传统的考试一直存在重结果、轻过程，重知识再现、轻探索发现的弊端，长此以往会扼杀学生的探索精神。在新课改的背景下，要扭转这种局面，教师必须将过程与结果、知识再现与探索发现摆在同等重要的位置，激发学生的创新意识。

例如，同学们把正方形桌子拼成一行，1张正方形的桌子可以围坐8人，2张正方形桌子拼好后可以围坐12人，3张正方形桌子拼好后可以围坐16人，以此类推。现在如果桌子數用a表示，学生人数用b表示，请用公式表示桌子数与学生人数之间的关系，并求出25张正方形桌子拼好后能坐多少人。

这道题不仅考查学生对已学知识的掌握程度，而且引导学生自主建构数学模型并加以运用，有助于培养学生的探究能力和创新能力。

四、突显衔接性，促进知识沟通

教师不仅要考查学生对小学数学的重要内容的掌握情况，还需要做好小学数学与初中数学的衔接工作，为学生的后续学习打下坚实的基础。

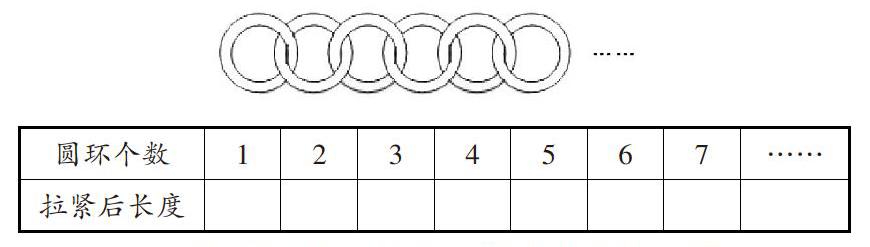
例如，现有若干个圆环，圆环的外直径为5厘米，环宽为5毫米，将它们连接后再测其长度，如下表：

（1）运用所学知识，完成表格中未填的部分。 

（2）根据表中呈现的规律，请计算出9个圆环拉紧后的长度是多少。

（3）假设圆环的个数为n，拉紧后总长度为S，用一个关系式进行归纳。

（4）如果连接后拉紧的长度是97厘米，它是由几个圆环组成的？

这道题不仅考查学生运用所学知识解决问题的能力，还涉及初中代数问题。学生通过自主观察、分析、归纳和猜想，就能够发现题目蕴含的数学规律，并熟练运用此规律解决问题。

总之，小学数学试卷命题工作必须与时俱进，随着课程标准、课程理念的转变而转变，只有这样才能适应课程改革的发展目标，促进学生全面发展。

[ 参 考 文 献 ]

[1] 陈明新.小学数学试题改革的探索[J].数学教学通讯，2016（11）.

[2] 杜和华.改革数学试题，促进素养提升[J].数学教学通讯，2017（8）.

（责编 童 夏）