影响汽车行业销量的因素分析?

摘 要：汽车行业的飞速发展，使其很快成为社会主流行业，本文通过公开的数据整理、分析、修正，总结了销售量、4S店、用户关注度、汽车型号之间的关系，为汽车行业的发展给出一些参考性建议。

关键词：汽车行业;销售量;数据分析;影响因素

一、背景介绍

中国汽车产业是继中国通信行业之后又一个高速发展的行业，中国的汽车行业自2000年前后起步，先后跨越了几个大发展阶段，至2009年，产销自百万级跨越到千万级;至2017年又跨越到近3000万级;2017年汽车经销市场总销售额近4万亿，形成了巨大的行业规模。汽车行业有多种不同的分类方法，按照用途汽车可分为乘用车、客车、货车、牵引汽车等，经过了几十年的发展，到目前品牌汽车品牌种类繁多，形成了国内国外上百种，包括国内外知名的劳斯莱斯、路虎、奔驰、宝马等到国内新崛起的吉利、比亚迪、奇瑞等，中国已经成为全球最大的汽车生产和销售大国。

二、研究的目的

汽车行业的发展离不开汽车政策、品牌、新车研发、市场销售、售后服务等各个方面，而品牌汽车的销量和销售额则是汽车行业研究的重要内容，找出影响汽车行业销量和销售额的因素对于整个汽车行业的发展有重要意义。

由于数据及收集的限制，本文在此仅通过公开发布的数据，在小范围内根据已有数据讨论主要的汽车品牌的销量与该品牌4s店数量、用户对该品牌关注度的排名、该品牌汽车的型号数量之间的关系，给出影响品牌汽车销量的相关因素的模型及数据化分析。

本文数据全部来自于公开的国家数据发布、行业协会、汽车行业垂直网站等给出的数据整理与引用。

三、模型设计及数据整理

通过对行业数据的整理，根据相关数学模型分析，建立如下的模型：Y=β0+β1.X1+β2.X2+β3.X3+μ

参数说明：

Y——2017年品牌汽车的销售量/单位辆

X1——品牌汽车全国4S店数量/单位个

X2——用户对汽车品牌的关注度排名指数

X3——汽车品牌的车型数量/单位个

以下为收集的公开发行的汽车行业垂直站点的部分数据，如下（该数据的原始数据可能为单独的相关数据，在此经过了汇总、整理，数据仅仅用于证明本文提出的相关论点的相关性）：数据以销量-y，全国4S店数量-X1，品牌关注度-X2，车型数量-X3为维度，品牌包括大众（3115228，2060，29140738，39）本田（1394328，1188，12226390，18）、别克（1260304，819，18743098， 12）、吉利（1247516，1000，6790828，17）、丰田（1131618，1229， 13836658，44）、日产（1117538，1031，9771784，27）、宝骏（1016232， 510，3930124，9）、五菱汽车（875478，512，1412620，10）、哈弗（851855，501，7155874，13）、福特（832919，835，6521416，31）、现代（781503，815，8165608，23）、长安（771549，444，9619522，19）、雪佛兰（601724，629，6195640，16）等近百家数据为依据（限于篇幅，以下数据省略）。数据来源：中国汽车工业协会、中国产业信息、车主之家等，本文数据有些在上述来源的基础上做了汇总。

四、数据分析及结论

本次数据模型使用相关软件进行分析，首先导入数据，其次拟合多元线性回归模型，并绘制残差散点图，观察效果。具体步骤如下：

以不同品牌汽车的销售量为因变量，品牌汽车全国4S店的数量、用户对汽车品牌的关注度排名指数、汽车品牌的的车型数量为自变量进行分析如下：分析-回归-线性，统计、图、保存（设置为保存残差）做设置（限于篇幅，图片省略）。

1.基本分析

经过上述数据设置、导入、分析，得到如下结果，并对结果做相关分析：

R数值为0.941，R方为0.885，调整好的R方为0.881，标准估算的误差为154580.626

a.預测变量：（常量），车型数量-X3，全国4S店数量-X1，品牌关注度-X2

b.因变量：销量-Y

从数据可以看出，模型拟合优度R2的值为0.885，经调整后的R2为0.881，远大于0.5，拟合优度比较好，线性明显，说明相关度较强。

2.模型的总体显著性检验数据

ANOVAa数据表中：

回归的平方和、自由度、均方分别为：16025059678957.326、 3、5341686559652.442，残差的平方和、自由度、均方分别为：2078879779057.667、87、23895169874.226。

总计的平方和、自由度分别为：18103939458014.992、90。

F值为223.547，显著性为.000b。

a.因变量：销量-Y

b.预测变量：（常量），车型数量-X3，全国4S店数量-X1，品牌关注度-X2

模型的总体显著性检验数据中，F值为223.547，p值远小于0.05，通过F检验，故拒接原假设，说明模型是显著的。

经过模型中，除了常量，三个系数：全国4S店数量-X1的t值为5.780，品牌关注度-X2的t值为10.461，车型数量-X3的t值为-2.884，三个系数的p值都远小于0.05，拒绝原假设H0，通过了t检验，模型显著。

下面对异方差进行检验，首先通过保存的残差RES_1，并做残差的绝对值保存到新变量e2，做spearman相关系数检验：得到新的分析图：根据上述设置及分析，得到如下的分析结果：

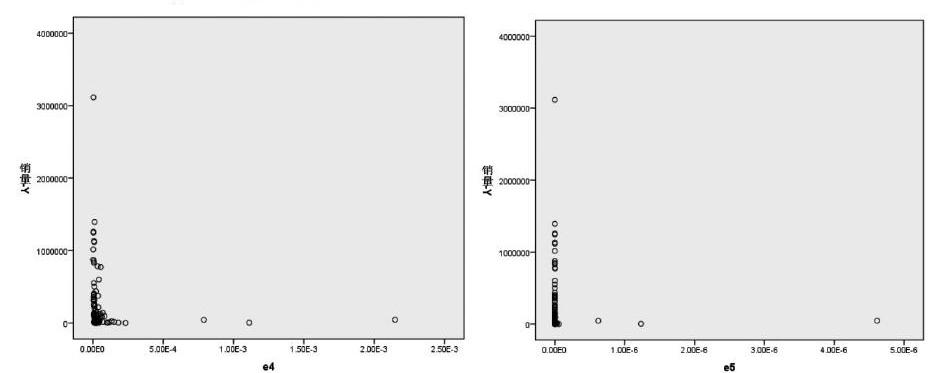
斯皮尔曼相关系数为0.580，大于0.5，p值远小于0.05，显著性明显，说明存在异方差，需要消除异方差，具体步骤如下：对残差绝对值取倒数，得到新的e4，并绘制散点图：随后对残差平方取倒数，得到新的e5，并绘制散点图。通过上述措施，基本消除了喇叭口，即消除了异方差。

消除了异方差，还需要做多重共线性的诊断，得到的结果如下：

模型显示，车型数量-X3容差为0.541，VIF为1.847，小于3，存在多重共线性的可能性较小;全国4S店数量VIF为3.302，品牌关注度VIF为3.337，存在多重共线性的可能性较大，需要采取措施消除多重共线性，采用步进法消除多重共线性，得到的三个模型的结果分别如下：

模型1：R数值为0.861，R方为0.741，调整好的R方为0.738，标准估算的误差为229656.468

模型2：R数值为0.935，R方为0.874，调整好的R方为0.871，标准估算的误差为160879.347

模型3：R数值为0.941，R方为0.885，调整好的R方为0.881，标准估算的误差为154580.626

a.预测变量：（常量），全国4S店数量-X1

b.预测变量：（常量），全国4S店数量-X1，品牌关注度-X2

c.预测变量：（常量），全国4S店数量-X1，品牌关注度-X2， 车型数量-X3

上图可以看出，第三个模型的调整后的R方为0.881最大，说明模型3的拟合程度最好。

3.ANOVAa数据分析

模型1的回归平方和、自由度、均方、F及显著性分别为：13409893169269.041、1、13409893169269.041、254.254、0.000

残差的平方和、自由度、均方分别为：4694046288745.951、 89、52742093131.977

总计的平方和、自由度、均方分别为：18103939458014.992、90

模型2的回歸平方和、自由度、均方、F及显著性分别为：15826308996401.127、2、7913154498200.563、305.738、0.000

残差的平方和、自由度、均方分别为：2277630461613.865、 88、25882164336.521

总计的平方和、自由度、均方分别为：18103939458014.992、90

模型3的回归平方和、自由度、均方、F及显著性分别为：16025059678957.326、3、5341686559652.442、223.547、0.000

残差的平方和、自由度、均方分别为：2078879779057.667、 87、23895169874.226

总计的平方和、自由度、均方分别为：18103939458014.992、90

a.因变量：销量-Y

b.预测变量：（常量），全国4S店数量-X1

c.预测变量：（常量），全国4S店数量-X1，品牌关注度-X2

d.预测变量：（常量），全国4S店数量-X1，品牌关注度-X2， 车型数量-X3

4.系数a数据分析

模型1：（常量）的t值为0.999，显著性为0.321;的品牌关注度-X2：t为21.479，显著性为0.000;

模型2：（常量）的t值为-2.130，显著性为0.036;的品牌关注度-X2：t为9.662，显著性为0.000;全国4S店数量-X1：t为5.012，显著性为0.000;

模型3：（常量）的t值为-.696，显著性为0.488;的品牌关注度-X2：t为10.461，显著性为0.000;全国4S店数量-X1：t为5.780，显著性为0.000;车型数量-X3：t为-2.884，显著性为0.005;

a.因变量：销量-Y

系数表里除常量外，其他各模型的所有系数的p值都远远小于0.05，说明显著性明显。

五、分析总结

根据以上的数据、设置、分析、修正，可以得出如下的结论：

1.结论一

模型3的调整后的R方为0.881，拟合程度明显，根据模型3建立的多元线性回归方程为：Y=-18483.253+493.856.X1+0.069.X2-6075.854.X3

说明品牌汽车的全国销量与该品牌全国的4s店的部署总数量关系非常密切，与用户对品牌的关注度的关系不是很大，而且与该汽车品牌的车型数量有较大的负相关性。

2.结论二

根据共线性的VIF值可以看出，模型3的VIF比较大，也可以选择模型2，而且模型2的调整后的R方为0.871，拟合程度与模型3相差不大，故若选择模型2，根据模型2建立的多元线性回归方程为：Y=-52703.385+430.880.X1+0.064.X2

该模型同样说明品牌汽车的全国销量与该品牌全国4s店的总数量关系密切，而与用户对品牌的关注度关系不是很大。

总之，本文仅仅讨论品牌汽车的销量与用户关注度及汽车型号之间的关系，不涉及其他要素的关联。根据上述数据分析，得出如下结论：

品牌汽车的全国销量的提升与该品牌全国4S店的部署总数有直接关系，与用户对该品牌的关注度没有直接关系，与该汽车品牌的车型数量可能有较大的负相关性。

参考文献：

[1]杨震，著.《基于数据的战略决策/数据模型与决策》.

[2]数据来源：中国汽车工业协会;中国产业信息;车主之家.

作者简介：王吉浩（1973.07- ），男，汉族，山东省烟台市人，大学本科学历，学士学位，对外经济贸易大学国际商学院企业管理专业在职课程研修班，现攻读对外经济贸易大学企业管理硕士学位