Third Hankel Determinant for the Inverse of Starlike and Convex Functions
Guo Dong, Ao En, Tang Huo and Xiong Liang-peng
(1. Foundation Department, Chuzhou Vocational and Technical College,Chuzhou, Anhui, 239000)
(2. School of Mathematics and Statistics, Chifeng University, Chifeng,Inner Mongolia, 024000)
(3. School of Mathematics and Statistics, Wuhan University, Wuhan, 430072)
Communicated by Ji You-qing
Abstract: Denote S to be the class of functions which are analytic, normalized and univalent in the open unit disk U = {z : |z| < 1}. The important subclasses of S are the class of starlike and convex functions, which we denote by S∗and C.In this paper, we obtain the third Hankel determinant for the inverse of functions f(z) = z +anzn belonging to S∗and C.
Key words: analytic function; third Hankel determinant; inverse of starlike function;inverse of convex function
1 Introduction
Let H(U) denote the class of functions which are analytic in the open unit disk U = {z : |z| <1}. Let A be the class of all functions f ∈H(U) which are normalized by f(0) = 0 and f′(0) = 1 and have the following form:

We denote by S the subclass of A consisting of all functions in A which are also univalent in U.
In [1] and [2], the q-th Hankel determinant for q 1 and n 1 is stated by Pommerenke as

where n, q ∈N+.
Following Pommerenke, many authors focused on the investigating of the second Hankel determinant H2(2) = a2a4−(see [3]–[6]). Only a few papers have been devoted to the third Hankel determinant (see [7]–[11])

We seek upper bound on the third Hankel determinant for the inverse of the classes S∗of starlike functions and C of convex functions. The class S∗and C are defined as follows.
Definition 1.1Letfbe given by(1.1).Thenf ∈S∗if and only if

Definition 1.2Letfbe given by(1.1).Thenf ∈Cif and only if

Let P be the class of all function p ∈H(U) satisfying p(0) = 1 and Re{p(z)} > 0. The function p ∈P have the following form:

In [7], it was proved that
Theorem 1.1

Lemma 1.1[12]Ifp ∈P,then the sharp estimate|pn| 2holds forn = 1, 2,··· .
Lemma 1.2[13]Ifp ∈P,then the following estimates holds forn, k = 1, 2,··· , n > k:

2 Main Results
Theorem 2.1Iff ∈S∗andf−1(ω) = ω +dnωnis the inverse function offwith|ω| < r0wherer0is greater than the radius of the Koebe domain of the classf ∈S∗,then we have

Proof.From (1.3), it follow that f ∈S∗can be written in the form

where p belongs to the class P.
From (2.1) it follows that

As

is the inverse function of f, we have

From (2.3) and (2.4), we have

From (2.4) and (2.5), we get

By comparing the coefficients of z and z2, we get

From (2.2) and (2.6), we obtain

From (2.7) and (1.2), we get

where

Using triangle inequality and Lemma 1.2, we get Theorem 2.1.
Theorem 2.2Iff ∈Candf−1(ω) = ω +dnωnis the inverse function offwith|ω| < r0wherer0is greater than the radius of the Koebe domain of the classf ∈C,then we have
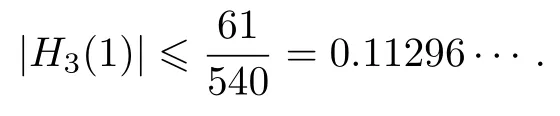
Proof.Similar approach as in the proof of Theorem 2.1. From (1.4), it follow that f ∈C can be written in the form

where p belongs to the class P. Equating coefficients in (2.8) yields

From (2.6) and (2.9), we get

From (2.10) and (1.2), we get

where

As above, it is enough to apply the triangle inequality and Lemmas 1.1 and 1.2.
 Communications in Mathematical Research2019年4期
Communications in Mathematical Research2019年4期
- Communications in Mathematical Research的其它文章
- Exact Solutions to the Bidirectional SK-Ramani Equation
- Global and Bifurcation Analysis of an HIV Pathogenesis Model with Saturated Reverse Function
- Global Existence and Blow-up for a Two-dimensional Attraction-repulsion Chemotaxis System
- Expanders, Group Extensions, Hadamard Manifolds and Certain Banach Spaces
- The Existence of Weak Solutions of a Higher Order Nonlinear Eilliptic Equation
- A Note on the Stability of K-g-frames
