The Existence of Weak Solutions of a Higher Order Nonlinear Eilliptic Equation

Liu Ming-ji and Liu Xu and Cai Hua

(1. School of Mathematics, Jilin University, Changchun, 130012)

(2. School of Applied Mathematics, Jilin University of Finance and Economics,Changchun, 130117)

Communicated by Li Yong

Abstract: In this paper, we show the existence of weak solutions for a higher order nonlinear elliptic equation. Our main method is to show that the evolution operator satisfies the fixed point theorem for Banach semilattice.

Key words: elliptic equation; Banach semilattice; fixed point; compressed mapping

1 Introduction and Main Result

In this paper, we consider the following elliptic problem:

where λ is a positive parameter, m ∈N, 0 < m <. We make the assumptions over V and h as:

(V) V (x) ∈C(RN, R+), and there exists an a ∈R such that

the index a describes the property of V near infinity, and we assume a > 2m.

(H) h : RN→R is a measurable function, and the function h(s) is nondecreasing on R, there exists a positive constant C such that h holds the growth condition:

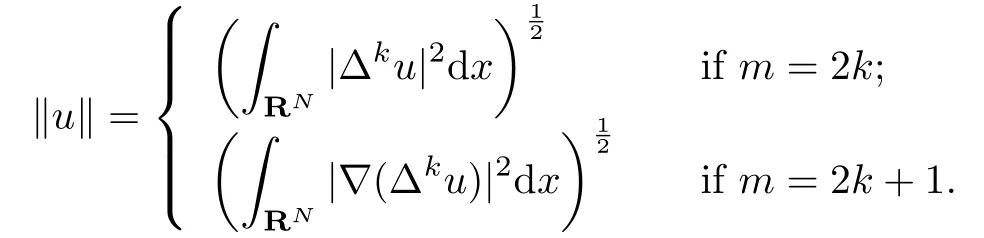
It is easy to see that the above norm comes from the scalar product

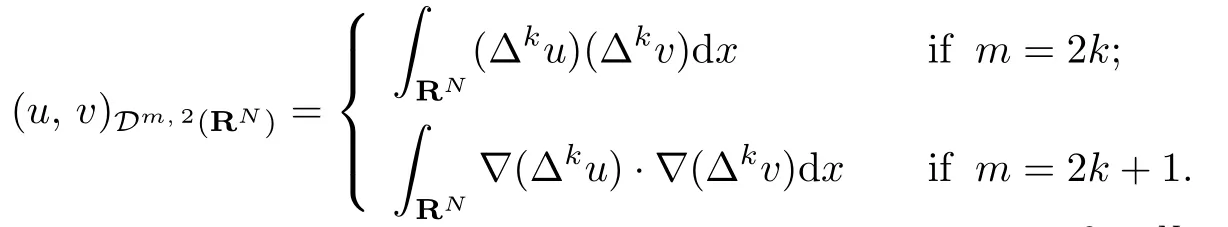
In this work, we consider our model problem in the working space Dm,2(RN).

The main result of the paper is the following theorem:

Theorem 1.1If the assumptions(V )and(H)hold,then there exists a positive constantλ∗> 0such that for any0 < λ < λ∗the model problem(Pλ)has a nontrivial weak solution.

There are many methods to study nonlinear elliptic equations, such as the theory of monotone operators, the Schauder’s fixed point theorem for compact mapping, the upper and lower solutions method, non-smooth critical point theories etc., we can see [1] for the choice of the method.

In this paper, we use the method introduced by Heikkil¨a[2]to show the existence of weak solutions of the elliptic problem, the main work is to show that the developed operator is increasing in order Banach spaces, then, due to the fixed point theorem, we get that the solution of the model problem is just the fixed point. The approach has been used in many work, one can see [3]–[9]. Here we give a solution in higher-order Sobolev space.

For the paper, the letter C is a positive constant which maybe variety at different lines.We denote the norm of the Lebesgue space Lp(RN) (1 < p < ∞) as

2 Preliminary

In this section, we give some preliminary results which are used later. Firstly, we give a special case of the result on Sobolev embedding which one can see [6].

Lemma 2.1The spaceDm,2(RN)is continuously embedding into the Lebesgue space

Next, we give the definition of weak solution of the problem (Pλ) in Dm,2(RN).

Definition 2.1A functionu ∈Dm,2(RN)is a weak solution of the problem(Pλ)if there holds

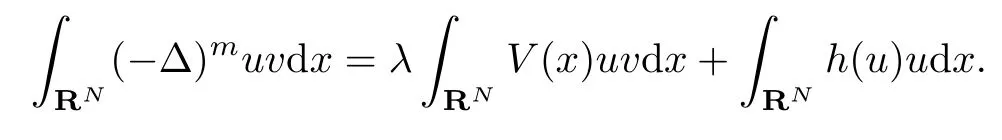
Due to the integral by part,the above equation implies

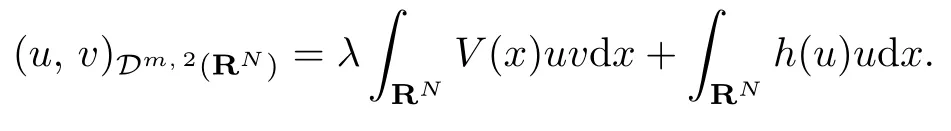
Now we give the concept of Banach semilattice, one can see [6]. Let X be a real Banach space. A nonempty set X+of X is said to be an order cone if the following conditions hold:

(i) X+is a convex and closed set;

(ii) for any u ∈X+and a real number β ≥0, βu ∈X+;

(iii) if u ∈X+and −u ∈X+, then u = 0.

A partial order in X derives from the order cone X+as: x ≺y if and only if (y−x) ∈X+,and (X, ≺) is called an ordered Banach space. If for any x, y ∈X, then inf{x, y} and sup{x, y} exist with respect to ≺, then we call X to be a lattice. Moreover, if for any x ∈X, we set x+= sup{x, 0} and x−= inf{x, 0}, the inequality ∥x±∥ ≤ ∥x∥holds, then we call (X, ∥ · ∥) to be a Banach semilattice.

Now suppose that (X, ≺) and (Y, ▹) are two ordered Banach spaces. We call an operator F : X →Y to be increasing if and only if for all x, y ∈X, x ≺y implies F(x) ▹F(y). A subset B of X is said to have fixed point property if every increasing operatorΛ: B →B has a fixed point.

Finally, we give the fixed point theorem due to Carl and Heikkil¨a[3]. We use this fixed point theorem to prove Theorem 1.1.

Theorem 2.1[3]SetXbe a Banach semilattice which is also reflexive. Then any closed ball ofXhas the fixed point property.

3 Proof of Theorem 1.1

In this section, we show the proof of Theorem 1.1. First we give a operator, and prove the operator is a contract mapping. For any λ > 0, we define the operator Tλ: Dm,2(RN) →(Dm,2(RN))∗as

where (Dm,2(RN))∗denotes the topological dual of Dm,2(RN). According to Riesz’s representation theorem, for u ∈Dm,2(RN) and λ > 0, there exists a unique element Lλu ∈Dm,2(RN) such that

Now we show that the operator Lλis a congruent mapping under some conditions.

Lemma 3.1Suppose that(V )and(H)hold. There exist two positive constantsλ∗andRsuch that for all0 < λ < λ∗,

holds,where

Proof.Set u ∈Dm,2(RN) and λ > 0. H¨older’s inequality implies

Now, due to the assumption (1.1), we know that if |x| > M, where M > 0 is large enough,then sup V (x)|x|a∼C, thus V (x) ≤C|x|−a, consequently,

where we used the continuity of the function V on the bounded domain {x ∈RN: |x| ≤M},and a > 2m. Next, by the condition (1.2), we have

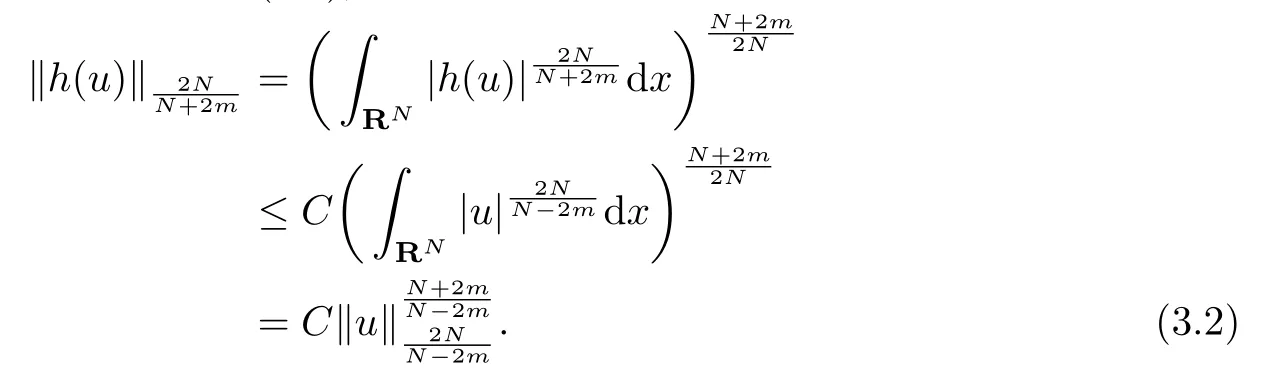
Combining (3.1), (3.2) and the embedding in Lemma 2.1

we obtain

where C1is a constant. Then we have

Now we choose 0 < R < 1 small enough, so that. We just choose

Then for all 0 < λ < λ∗,

Therefore we complete the proof of the lemma.

Now we show the proof of Theorem 1.1. We bring in the positive cone

to a partial order on Dm,2(RN) which is preserved by the operator Lλ. As in [6], we introduce another convex closed cone

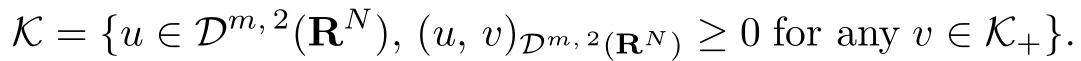
In [10], the dual cone of K+is

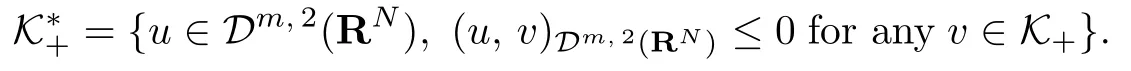
By the definition of the negative cone

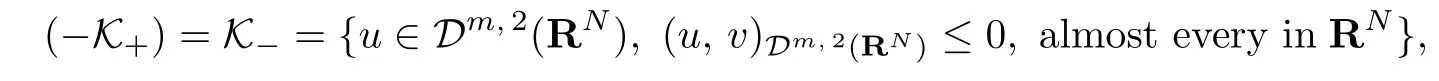
it is easy to see that

According to [6], we know that K is an order cone, and K induces a partial order in Dm,2(RN)as

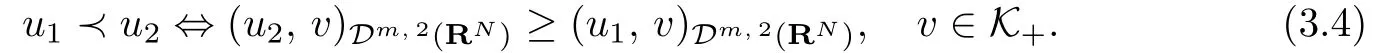
It is also known that K+is a convex closed cone of the Hilbert space Dm,2(RN) and Dm,2(RN) is a Banach semilattice.

Next we show that for any λ > 0, the operator Lλintroduced above is increasing from(Dm,2(RN), ≺) to (Dm,2(RN), ≺). Suppose that u1, u2∈Dm,2(RN) and they satisfy u1≺u2. Thus by (3.5), we have (u2−u1, v)Dm,2(RN)≥0 for any v ∈K+, which implies(u1−u2, v)Dm,2(RN)≤0 for any v ∈K+. By the relation (3.4), we have u1−u2∈⊂K−,which means u1≤u2, a.e., x ∈RN. Hence, due to V ≥0, λ > 0 and the assumption (H)over the function h, we obtain that

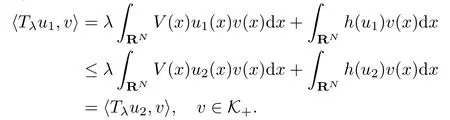
That means that for any v ∈K+, (Lλu1, v)Dm,2(RN)≤(Lλu2, v)Dm,2(RN), thus Lλu1≺Lλu2. Taking into Theorem 2.1 and Lemma 3.1 into account, we have that for any 0 < λ <λ∗, the operator Lλhas a fixed point, which is a weak solution of the problem (Pλ). And the weak solution is nontrivial due to the fact h≠ 0. Therefore we complete the proof of Theorem 1.1.