A Note on the Stability of K-g-frames
Xiang Zhong-qi
(College of Mathematics and Computer Science, Shangrao Normal University,Shangrao, Jiangxi, 334001)
Communicated by Ji You-qing
Abstract: In this paper, we present a new stability theorem on the perturbation of K-g-frames by using operator theory methods. The result we obtained improves one corresponding conclusion of other authors.
Key words: g-frame; K-g-frame; frame operator; stability
1 Introduction
A frame for a Hilbert space was discovered in 1950’s by Duffin and Schaeffer[1], which has made great contributions to various fields because of its nice properties, the reader can examine [2]–[8] for background and details of frames. G-frames, proposed by Sun[9],generalize the notion of frames extensively, which possess some distinct properties though they share many similar properties with frames (see [10] and [11]).
A K-frame is an extension of a frame, which emerged in the work on atomic systems for operators due to G˘avrut¸a[12], and the results involved show us that the properties of K-frames are quite different from those for frames owing to the linear bounded operator K(see also [13]–[16]).
The idea of G˘avrut¸a has been applied to the case of g-frames by Xiaoet al.[17]and thus providing us the concept of K-g-frames, which have already attracted many researchers’interest due to their potential flexibility (see [18]–[21] for example). In this paper we pay attention to the stability of K-g-frames, and the motivation derives from an observation on one stability result for K-g-frames, Theorem 4.1 in [21], recently obtained by Hua and Huang. In the proof the authors asserted that the frame operator of the involved K-g-frame is invertible on the whole space, which plays a key role in their proof to show the lower K-g-frame bound condition stated in the theorem. In reality, however, the invertibility of the frame operator of a K-g-frame is absent for the whole space, since a K-g-frame is not necessarily a g-frame (see Example 3.1 for details). The purpose of this paper is to provide an improvement to their result.
Throughout this paper, the notations H and K are reserved for two Hilbert spaces,and {Kj}j∈Jis used to denote a sequence of closed subspaces of K , where the index set J is finite or countable. The family of all linear bounded operators from H to K is designated as B(H , K ), which is abbreviated to B(H ) if H = K . The notation R(θ) designates the range of θ ∈B(H , K ).
Let ℓ2({Kj}j∈J) be the Hilbert space defined by

where the inner product is given by

For a sequence of linear bounded operators {Λj}j∈Jfrom H into Kj, let HΛbe the set defined by

2 Preliminaries
In this section we mainly collect some basic definitions and properties for K-g-frames.
Definition 2.1SupposeK ∈B(H ).One says that a family{Λj∈B(H , Kj)}j∈Jis aK-g-frame forHwith respect to{Kj}j∈Jif there exist0 < C ≤D < ∞such that

The constantsCandDare called,respectively,the lower and upperK-g-frame bounds.
Remark 2.1If K is equal to the identity operator on H , IdH, then a K-g-frame turns to be a g-frame.
In general, if {Λj}j∈Jsatisfies the inequality to the right in (2.1), we say that {Λj}j∈Jis a D-g-Bessel sequence for H with respect to {Kj}j∈J, associated with which there is a linear bounded operator, called the analysis operator of {Λj}j∈J, defined by

The adjoint operator

given by

is said to be the synthesis operator. A composition of U∗Λand UΛyields a positive and self-adjoint operator which we call the frame operator, given below

It is easy to check that SΛis invertible if and only if {Λj}j∈Jis a g-frame.
The following result tells us that we can naturally get a K-g-frame from a g-frame.
Proposition 2.1SupposeK ∈B(H ).Then every g-frame is aK-g-frame.
Proof.Let {Λj}j∈Jbe a g-frame for H with respect to {Kj}j∈Jwith bounds C, D and the frame operator SΛ. To prove that {Λj}j∈Jis a K-g-frame for H with respect to {Kj}j∈J,it only needs to show the lower bound inequality. For any f ∈H , we see from (2.3) that

and thus,

Now we compute that

It follows that

as desired.
Remark 2.2The converse of Proposition 2.1 is not true, please check Example 3.1.
Proposition 2.2[22]If Θ∈B(H , K )has closed range,then there exists a unique operator Θ†∈B(K , H )such that ΘΘ†Θ=Θ.
Lemma 2.1[23]Assume thatT : H →His a linear operator,and there are constantsλ, µ ∈[0, 1)satisfying

ThenT ∈B(H )and

3 The Main Result
The following result is presented in [21] as Theorem 4.1.
Theorem 3.1Suppose thatK ∈B(H )has closed range and{Λj}j∈Jis aK-g-frame forHwith respect to{Kj}j∈Jwith boundsCandD. Suppose that Γj∈B(H , Kj)for eachj ∈Jand there exist constantsλ1, λ2, µ 0such thatmax< 1and
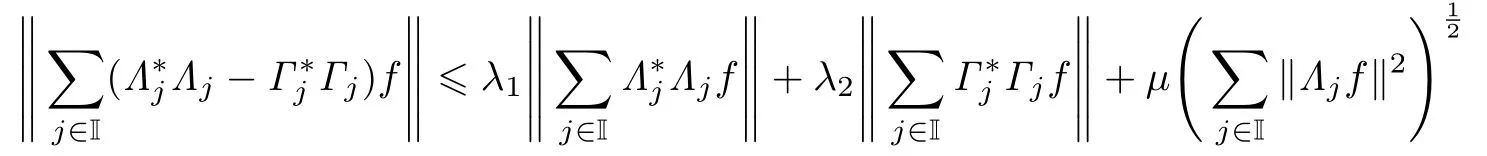
for any finiteI ⊂Jand anyf ∈H ,then{Γj}j∈Jis aK-g-frame forHwith respect to{Kj}j∈Jwith bounds

In the proof of the lower K-g-frame bound condition the authors of [21] asserted that the frame operator of the associated K-g-frame is invertible on H , implying that a K-g-frame is necessarily a g-frame, which is not true, as shown in the following example.
Example 3.1Let {ej}j∈Nbe an orthonormal basis for H and define

Clearly, K is well defined, linear bounded and self-adjoint. For j = 1, 2, 3,···, let Kj=and define linear bounded operatorΛj: H →Kjas follows:

It is easily seen that the adjoint operator: Kj→H is given by

For any f ∈H we have

Thus {Λj}j∈Nis a K-g-frame for H with respect to {Kj}j∈N.
We next show that {Λj}j∈Ndoes not satisfy the lower bound inequality of a g-frame.Assume on the contrary that there exists a constant C > 0 such that

Let k ∈N be a positive integer which is greater than. Noting that (2k−1)e2k−1∈K2k−1, we have
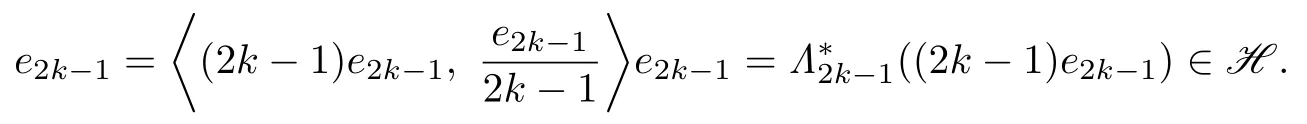
Therefore,
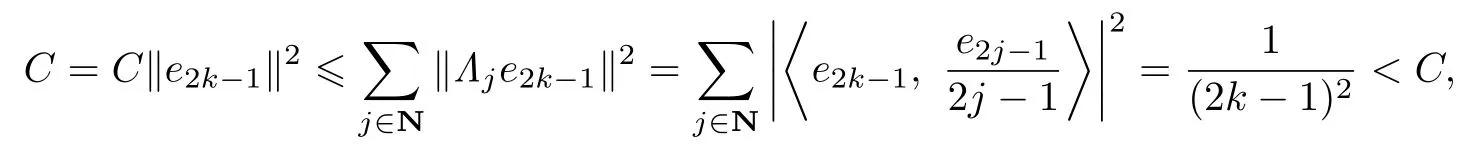
a contradiction.
Suppose that K ∈B(H ) and {Λj}j∈Jis a K-g-frame for H with respect to {Kj}j∈Jwith bounds C, D and the frame operator SΛ. From Example 3.1 we know that SΛis not an invertible operator on H in general. We show, however, that it can be invertible on the subspace R(K), provided K has closed range. Indeed, since R(K) is closed, from Proposition 2.2 it follows that

namely,


From this and taking into account that

we obtain
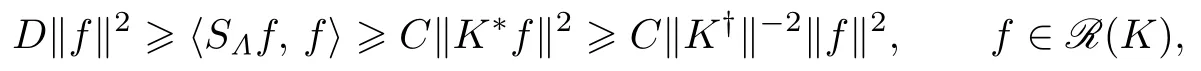
implying that SΛ: R(K) →SΛ(R(K)) is homeomorphous. Hence

Now we can improve Theorem 3.1 as follows.
Theorem 3.2Suppose thatK ∈B(H )has closed range and{Λj}j∈Jis aK-g-frame forHwith respect to{Kj}j∈J.LetC, DandSΛbe the bounds and the frame operator of{Λj}j∈J,respectively.Suppose that Γj∈B(H , Kj)for eachj ∈Jand thatR(K), HΓ⊂SΛ(R(K)).If there exist constantsλ1, λ2, µ ≥0such thatmax< 1andf

or any finiteI ⊂Jand anyf ∈H ,then{Γj}j∈Jis aK-g-frame forHwith respect to{Kj}j∈Jwith bounds

Proof.For any finite I ⊂J and any f ∈H we have

It follows that

where in the second inequality we apply the fact that



meaning that {Γj}j∈Jis a-g-Bessel sequence for H with respect to{Kj}j∈J. Note that for any f ∈H we also have

Then for each g ∈SΛ(R(K)), takingg instead of f in above equation we get

Hence by Lemma 2.1,

is invertible with

Now for any g ∈SΛ(R(K)),

Therefore,

Since every f ∈H has a composition as f = g + h, where g ∈SΛ(R(K)) and h ∈(SΛ(R(K)))⊥, and∈SΛ(R(K)), it follows that

Noting also that h ∈(SΛ(R(K)))⊥⊂(R(K))⊥, we have

Thus

Altogether we know that

for every f ∈H , and the proof is finished.
 Communications in Mathematical Research2019年4期
Communications in Mathematical Research2019年4期
- Communications in Mathematical Research的其它文章
- Exact Solutions to the Bidirectional SK-Ramani Equation
- Global and Bifurcation Analysis of an HIV Pathogenesis Model with Saturated Reverse Function
- Global Existence and Blow-up for a Two-dimensional Attraction-repulsion Chemotaxis System
- Expanders, Group Extensions, Hadamard Manifolds and Certain Banach Spaces
- The Existence of Weak Solutions of a Higher Order Nonlinear Eilliptic Equation
- Third Hankel Determinant for the Inverse of Starlike and Convex Functions
