Exact Solutions to the Bidirectional SK-Ramani Equation

Zou Jia-hui and Wang Yun-hu

(1. College of Science, University of Shanghai for Science and Technology, Shanghai, 200093)(2. College of Art and Sciences, Shanghai Maritime University, Shanghai, 201306)

Communicated by Gao Wen-jie

Abstract: In this paper, the bidirectional SK-Ramani equation is investigated by means of the extended homoclinic test approach and Riemann theta function method, respectively. Based on the Hirota bilinear method, exact solutions including one-soliton wave solution are obtained by using the extended homoclinic approach and one-periodic wave solution is constructed by using the Riemann theta function method. A limiting procedure is presented to analyze in detail the relations between the one periodic wave solution and one-soliton solution.

Key words: Hirota bilinear method; bidirectional Sawada-Kotera equation; extended homoclinic test approach; Riemann theta function

1 Introduction

In this paper, we focus on the following nonlinear evolution equation (NLEE)

which was formulated in [1] as a bidirectional counterpart of the classical Sawada-Kotera(SK) equation

It has been shown that the bilinear form of equation (1.1) is identical to the well-known Ramani equation (see [2]). Therefore, equation (1.1) is also called bSK-Ramani equation(see [3]). In [4], the quasi-multisoliton and bidirectional solitary wave solutions of bSKRamani equation (1.1) are obtained by using the Hirota’s direct method (see [5]). In [6], its periodic solitary wave solutions are obtained by means of Hirota’s direct method and ans¨atz function method. In [7], the Adomian decomposition method is also used to construct the soliton solutions and doubly-periodic solutions of bSK-Ramani equation (1.1).

It is well known that the Hirota’s direct method (see [5]) is a powerful tool to construct exact solutions for NLEEs. Once a NLEE is written in bilinear forms, then multi-soliton solutions and rational solutions can be obtained. In [8] and [9], the Hirota’s method is extended to directly construct periodic wave solutions of NLEEs with the help of Riemann theta functions. To our knowledge, there is no literature to investigate bSK-Ramani equation(1.1) by using Riemann theta functions. In this paper, based on a more general bilinear form of bSK-Ramani equation (1.1), we give some exact solutions by using the Riemann theta functions method (see [8]–[9]) and extended homoclinic test approach (see [6], [10]–[11]).

The organization of this paper is as follows. In Section 2, some exact solutions of bSKRamani equation (1.1) are obtained by using Hirota’s direct method and extended homoclinic test approach. In Section 3, one-periodic wave solution of bSK-Ramani equation (1.1)is obtained with the help of Riemann theta function method. Moreover, a limiting procedure is applied to analyze asymptotic behaviour of the one-periodic wave solution, it is proved that the one-periodic wave solution tends to the one-soliton solution. Some conclusions are provided in Section 4.

2 Extended Homoclinic Test Approach to bSK-Ramani Equation (1.1)

In [6], Liu and Dai obtained some exact and periodic solitary wave solutions of bSK-Ramani equation (1.1) with its bilinear form expressed as

where the bilinear operator D is defined by

By the following transformation

where u0is a constant solution of bSK-Ramani equation (1.1), then equation (1.1) can be translated into the following bilinear form

in which c is an integration constant. Assuming c = 0, yields

Based on the extended homoclinic test approach (see [6], [10] and [11]), we suppose that the solution of equation (2.5) takes the form

where ξj= κjx + ωjt + δj, and κj, ωj, cj(j = 1, 2, 3) are constants to be determined, δjare free constants. Substituting the ans¨atz equation (2.6) into the bilinear equation (2.5)and equating all the coefficients of different powers of e−ξ1, eξ1, cos(ξ2), sin(ξ2), cosh(ξ3),sinh(ξ3) and constant term to zero, we get a set of algebraic equations for κj, ωj, cj. By solving this system with the aid of Maple, we get the following results:

Case 1.

By choosing κ2as a real number and c3= 1, f can be written as

which corresponds to one-periodic solution of bSK-Ramani equation (1.1) as

When κ2= ik2, k2is a real number and c3= 1, f can be written as

which corresponds to one-soliton solution

it allows wave velocity different from the ones

with phase variable

in [1].

Case 2.

When u0> 0, f can be written as

Substituting expression (2.14) into (2.3), we obtain

When c3= 1, we obtain the one-soliton solution

When u0< 0 and c3= 1, f can be written as

which corresponds to one-periodic solution

In Case 2, it is clear that the amplitude and wave speed are completely determined by the constant solution u0.

3 One-periodic Wave Solution and Asymptotic Properties to bSK-Ramani Equation (1.1)

3.1 Construction of One-periodic Wave Solution

Nakamura[12]-[13]developed a direct way to construct a kind of quasi-periodic solutions of NLEEs via Hirota bilinear method and Riemann theta function. More recently, this method is extended to investigate NLEEs include both continuous and discrete ones (see [8], [9],[14]–[16]). In the following, we construct the one-periodic wave solution of bSK-Ramani equation (1.1) by this method and discuss its asymptotic property in detail.

In the process of constructing quasi-periodic wave solutions, the nonzero constant c in(2.4) plays an important role. The Riemann theta function of genus N reads

where the integer vector n = (n1,··· , nN)T∈ZN, and phase variable ξ = (ξ1,··· , ξN)T∈CN. For two vectors f = (f1,··· , fN)Tand g = (g1,··· , gN)T, their inner product is defined by

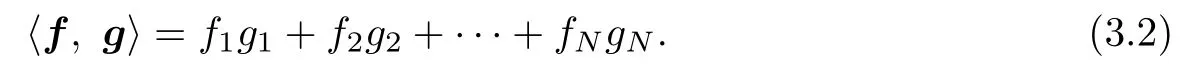
When N = 1, the Riemann theta function (3.1) becomes

where ξ = κx + ωt + δ and τ > 0. To construct one-periodic wave solution, the function f in (2.4) can be taken as

It is well known that the Hirota operator D has the following property:

where G(Dx, Dt) is a polynomial about Dxand Dt. Substituting expression (3.4) into (2.4)with (3.5) leads to

where the coefficient of e2πim′ξis denoted as

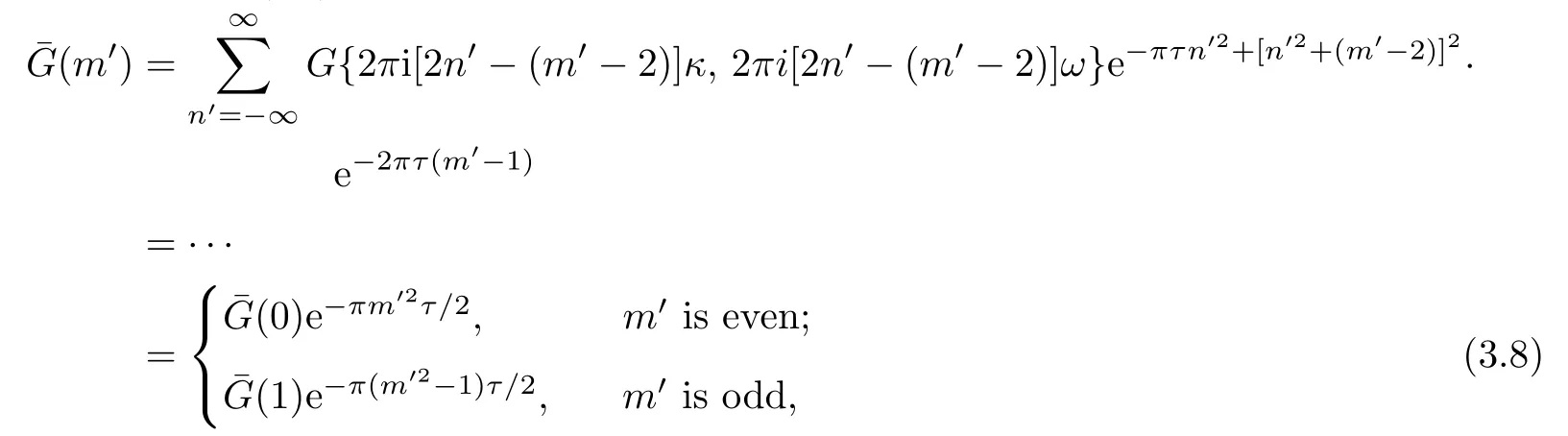
are satisfied, then it follows that(m′) = 0, m′∈Z, and the function (3.4) is just the solution for (2.4), namely,

Combining (3.7) and (3.9) yields

By introducing the notations as

then system (3.10) and (3.11) are simplified into a linear system for the frequency ω and the integration constant c and η, namely

There are only two constraint equations with three constants ω, c and η in system (3.13),however, thanks to the third constraint equation

we have

with

Now we obtain a one-periodic wave solution of bSK-Ramani equation (1.1)

where ϑ(ξ) and ω are given by (3.4) and (3.15), respectively. The other parameters κ, δ, τ,u0are free. Fig. 3.1 shows the one-periodic wave (3.17) for proper choices of parameters.

Fig. 3.1 A one periodic wave of bSK-Ramani equation (1.1) via expression (3.17)

3.2 Asymptotic Property of One-periodic Wave Solution (3.17)

In the following, we consider asymptotic properties of the one-periodic wave solution (3.17).Since both the coefficient matrix and the right-side vector of system (3.13) are power series of λ, its solution (ω, η, c)Tcan be written as a power series of λ. We can solve system (3.13)through small parameter expansion method, the general procedure is described as follow.We write the system (3.13) into power series of λ:

where

from which we can recursively get each vector Xk, k = 0, 1,··· .

If the matrix A0is reversible, solving relations (3.20) yields

If A0and A1are not reversible, but they take the following form

considering the third constraint equation

and comparing the coefficient of same power of λ in (3.22), we get

Solving relations (3.20) with (3.21) and (3.23) yields

where V(I)and V(II)denote the the first and second component of a two-dimensional vector V respectively, and

The relation between the one-periodic wave solution (3.17) and the one-soliton solution(2.12) can be established as follows.

With the help of (3.12) with (3.18), we write aij, bi, i = 1, 2, j = 1, 2, 3 as the series of λ

then, we have

and

Substituting (3.26) and (3.27) into (3.24), we get Xk(k = 0, 1, 2,···), and thus

which implies that by setting u0= 0

To show that the one-periodic wave (3.17) tends to the one-soliton solution (2.12), under the transformation

the theta function (3.4)

can be written as

Combing (3.28) and (3.29) deduces that

or, equivalently,

(3.32) immediately leads to

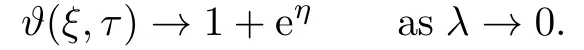
From above, we conclude that the one-periodic wave (3.4) tends to the one-soliton solution(2.12) as the amplitude λ →0.

4 Conclusions

The investigation on various exact solutions of NLEEs is very important in nonlinear science(see [17]). In this paper, based on the bilinear equation (2.4), the extended homoclinic test approach and Riemann theta function method are applied to construct exact solutions of the bSK-Ramani equation (1.1), respectively. With the help of the Riemann theta function and Hirota bilinear method, the one periodic wave solution (3.17) of the bSK-Ramani equation(1.1) is obtained. A limiting procedure is presented to analyze asymptotic behaviour of the one-periodic wave, it is proved that the one-periodic wave solution (3.17) tends to the one-soliton solution (2.12) under small amplitude limit. It should be noted that the system(3.13) is different from the general form in [8]–[9], [14]–[16] and [18]–[19]. However, it is difficult to construct the two-periodic wave solution of the bSK-Ramani equation (1.1), the reason is that the term D2tin bilinear equation (2.4). How to construct two-periodic wave solution for this type of bilinear equation by Riemann theta function method is worthy of further study.