The Homotopy Perturbation Renormalization Group Method to Solve the WKB Problem with Turn Points
Lü Yue, Zhao Xu-tong and Liu Ming-ji
(School of Mathematics, Jilin University, Changchun, 130012)
Communicated by Li Yong
Abstract: In this paper, we give the homotopy perturbation renormalization group method, this is a new method for turning point problem. Using this method, the independent variables are introduced by transformation without introducing new related variables and no matching is needed. The WKB approximation method problem can be solved.
Key words: homotopy movement; renormalization group method; turn point WKB problem
1 Introduction
Perturbation method is widely used in solving nonlinear problems (see [1]), but for some problems the expansions of solutions are inconsistent. In order to overcome inconsistency,scholars have developed many singular perturbation techniques, and WKB method (see [2]–[3]) is one of the effective methods. WKB approximation method theory is a well-known powerful tool for obtaining global approximate solutions of linear differential equations.Many linear problems often solved by boundary layer theory can also be solved by WKB theory. The limitation of the WKB method is that it can only be applied to linear equations. The standard WKB approximation fails near the turning point. By using Langer or Liouville-green transformation, an effective expansion including turning points can be obtained. However, for transformations such as Liouville-green and Langer, interdependent scaling variables are introduced into the transformation process. These variables are not easy to select, and also make the calculation cumbersome. In 1998, He[4]combined the perturbation method with the homotopy method and proposed the homotopy perturbation method. The homotopy perturbation method can be used to solve the nonlinear problems effectively (see [5]–[7]). In order to overcome the above difficulties, inspired by the perturbed renormalization group theory (see [8]–[9]) and the homotopy perturbation method,we propose the homotopy perturbation renormalization group method in this paper. We use homotopy renormalization group method by independent variables through transformation to easily solve the problem of WKB approximation without introducing new related variables and matching. Therefore, many WKB approximation method or multi-scale analysis of dynamics quantum problems can also be solved by the homotopy renormalization group method. In this paper, we use homotopy renormalization group method to solve the WKB problem with turning point.
2 The Homotopy Perturbation Renormalization Group Method
In 1915, Gans[10], a physicist, studied the propagation of light in inhomogeneous media and got typical equation from the Maxwell equation. We consider the following typical equation of WKB problem with turning point:

where ϵ is a small parameter.
We make the following assumptions:
(C1) The equation (2.1) has solutions under the initial condition (2.2);
(C2) There are isolated zeros at x = 0 of Q(x), let Q(x) = xαφ(x), where φ is a positive function.
The system (2.1)–(2.2) is studied by using homotopy permutation renormalization group method. We firstly construct uniform effective evolutionary expansion as the solution of equation (2.1). We introduce new independent variables t, bydx, we have

The equation (2.1) is transformed into

where

When x →0, t ∼x, so S is bounded near x = 1. To simplify, we consider the case of α = 1.
We study the system (2.4) by homotopy perturbation renormalization group method,and construct the uniformly valid asymptotic expansion of its solution.
Define the following auxiliary linear operator:

the operator has property
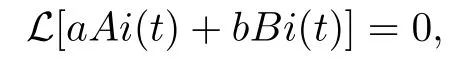
where a and b are constants and Ai and Bi are Airy functions. For (2.4), when ϵ →0 we consider the conditions u(+∞) = 0 without Bi(t). We take

as the initial guess solution of u(t), where C0is a constant, it is determined by the initial condition. We define non-linear operator

where p ∈[0, 1]. Construct homotopy mapping
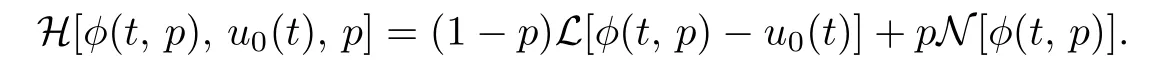
Let

We have homotopy equation

When the embedded variable p increases from 0 to 1, the value of ϕ(t, p) is continuously from the initial guess solution of u0(t) to the solution of the original equation u(t). We write the solution of the equation ϕ(t, p) in series form with respect to p,

Then the approximate solution of equation (2.4) is

We compare the coefficients p at both ends of the homotopy equation (2.6), we get

Put u0(t) = C0Ai(t) into (2.7), we have

So the first order approximate solution is

when t −t0→+∞,is limited. In order to make the expansions uniformly valid, we need to eliminate inconsistencies, and makerenormalized.
We introduce the free parameter τ, make transformation

where Zn, n = 1, 2,··· is a renormalization constant.
The term τ can be eliminated step by step for ϵ, and the renormalization constants can be determined. The decomposition integral interval is from t0to τ and from τ to t.
The first order approximate solution (2.9) is obtained

We eliminate the integral term from τ to t0, and determine the coefficient
10. None but a real Princess could have had such a delicate sense of feeling: While the modern implication of such a princess would be a high maintenance woman, another possible interpretation7 is that the woman is full of compassion15.
then the first order approximate solution is

There is no variable τ in the expansion of the original problem, so= 0. We have

For solving the renormalization group equation, let τ = t and t0= 0. We can get

Replace t = f(x), then the uniformly valid asymptotic solution of the equation (2.1) is obtained as follows.

where C(0) is determined by the initial value condition,

We find that the expression of C(t) contains the Airy function Ai and Bi, the results obtained by the homotopy perturbation renormalization group method are different from standard Langer formula. Notice that the new variable t is a function of ϵ, and for given x,when ϵ →0, t → ∞. From the asymptotic properties of Airy functions Ai and Bi, when t → ∞, Ai′(t)Bi(t) ∼ −π. So the result (2.12) contains the standard result

So we get the following theorem.
Theorem 2.1Assumptions(C1)and(C2)are valid, u(x)is the solution of(2.1).Then

whereAiandBiare Airy functions,
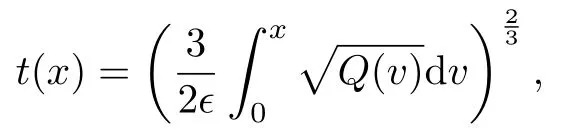
C = C(t, C(0), ϵ)is the solution of renormalization group equation

whereC(0)is determined by the initial condition(2.2).
3 Example
We consider the following time-dependent vibration systems with elastic constants

where ϵ is a small parameter. When t → ∞, the standard perturbation theory is invalid.Multiscale analysis can eliminate long-term behavior, however multiple time scales must be chosen as: τ0= t, τ1=, τ2= ϵt, ··· . Because the frequency of vibration depends on time, the conventional telescopic coordinate method fails. We find that O(), homotopy perturbation renormalization group method can provide uniformly valid solutions. It can be directly separated from the renormalization group process without specifying the time scale of slow change. But because of the singularity at ϵt = 1, it cannot give results that depend on the order of ϵt = 1. This problem is a WKB problem with turning point.
We use the homotopy perturbation renormalization group method to consider the results(3.1) depending on the order of ϵ−1.
Let x = ϵt. We convert the equation (3.1) into

where Q(x) = x−1, x = 1 is a first-order turning point. We introduce independent variables

so

The equation (3.3) is transformed into

where

From Theorem 2.1, the renormalization group equation is

We solve the renormalization group equation. Let τ =. We get

the uniform asymptotic expansion of (3.3) is

where C(0) is determined by the initial value condition. We replace x = ϵt, and get a uniform asymptotic expansion of (3.1).
 Communications in Mathematical Research2019年4期
Communications in Mathematical Research2019年4期
- Communications in Mathematical Research的其它文章
- Exact Solutions to the Bidirectional SK-Ramani Equation
- Global and Bifurcation Analysis of an HIV Pathogenesis Model with Saturated Reverse Function
- Global Existence and Blow-up for a Two-dimensional Attraction-repulsion Chemotaxis System
- Expanders, Group Extensions, Hadamard Manifolds and Certain Banach Spaces
- The Existence of Weak Solutions of a Higher Order Nonlinear Eilliptic Equation
- A Note on the Stability of K-g-frames
