Univalent Criteria for Analytic Functions Involving Schwarzian Derivative
Hu Zhen-yong, Wang Qi-han, He Liang-miao and Long Bo-yong
(School of Mathematical Sciences, Anhui University, Hefei, 230601)
Communicated by Ji You-qing
Abstract: In this paper, some new criteria for univalence of analytic functions defined in the unit disk in terms of two parameters are presented. Moreover, the related result of Aharonov and Elias (Aharonov D, Elias U. Univalence criteria depending on parameters. Anal. Math. Phys., 2014, 4(1-2): 23–34) is generalized.
Key words: analytic function; univalent function; Schwarzian derivative; univalent criteria
1 Introduction
An analytic function f(z) is said to be univalent in D = {z, |z| < 1} if it is one-to-one in D. As usual, for some simple analytic functions we may judge easily if it is univalent by definition. In fact, we are often faced with complicated analytic function, and it is hard to determine whether to be univalent. Therefore, judging only by definition is not enough. This allows scholars to explore other univalent criteria. Recently, some new univalent criteria for analytic functions have been established in [1]–[4].
The Schwarzian derivative of a locally univalent analytic function f(z) is defined by

The status of Sf(z)in the study of univalence is very important. Some classical univalent criteria over the Schwarzian derivative are introduced in the following. Nehari[5]proved that if

or

then f(z) is univalent in D. Later, Hille[6]proved the criterion (1.1) is sharp. Pokornyi[7]stated the criterion

But this proof of the result is due to Nehari[8].
In the spirit of Steinmetz[9], Aharonov[10]defined a result of sharpness of univalent criteria.
Theorem 1.1A criterion for univalence of the form|Sf(z)| 2p(|z|) (z ∈D)is sharp,if for an analytic functionf(z),the conditionsSf(x)2p(x),wherex ∈(−1, 1),andSf(x)≠ 2p(x)imply thatf(z)is not univalent inD.
Nehari[8]proved the following theorem, which provides a method to establish new results on univalent criteria.
Theorem 1.2Suppose that
(a) p(x)is a positive and continuous even function forx ∈(−1, 1);
(b) p(x)(1 −x2)2is nonincreasing forx ∈(0, 1);
(c)the differential equation

has a solution which does not vanish in−1 < x < 1.Then,any analytic functionf(z)inDsatisfying|Sf(z)| 2p(|z|)is univalent inD.
In view of Theorem 1.2, the univalent criteria (1.1), (1.2) and (1.3) can be given by

respectively.
Let p(z) be analytic in D and consider the analytic differential equation

Further, let u(z) and v(z) be two linearly independent functions (solutions of (1.5)). Under the assumptions of Theorem 1.2, if p(z) is self majorant (an analytic function p(z) in the open D is said to be self majorant, if |p(z)| p(|z|) for all z ∈D), then

satisfies

and f0(z) is univalent. Noting that

and

where W[u(z), v(z)] is the Wronskian determinant of u(z) and v(z), c1is a constant. Thus,we rewrite (1.6) as follows

Integrating on both sides of (1.7), we obtain

where c1, c2are constants. Thus, a special univalent function

is concluded.
Moreover, Steinmetz[9]proved that if p(z) is self majorant and

where y(x) is given by (1.4), then the criterion |Sf(z)| 2p(|z|) is sharp.
Nehari[11]proved a general condition for univalence of analytic functions in D as follows.

The criterion can be generated by the function

As to Schwarzian derivative of analytic functions, we refer to [12]–[15] for more details.
In the next section, we want to find a general p(x). In view of this point, we consider that

where y(x) is given by (1.4), a ∈, k is a parameter. In addition, for x ∈(−1, 1),Q(x, k)≠ 0 and is even, Q′′(x, k) is continuous for x ∈[−1, 1]. According to the fundamental conditions, we give a genernal p(x). Furthermore, we present some special p(x).
2 Main Results
Theorem 2.1Let

where, kis a parameter with
(i)Forx ∈(−1, 1), Q(x, k)≠ 0and is even;
(ii) Q′′(x, k)is continuous forx ∈[−1, 1];
(iii) p(z)is self majorant,wherez ∈D,andp(x)(1−x2)2is nonincreasing forx ∈(0, 1).Furthermore, iff(z)is an analytic function inDsatisfying|Sf(z)| 2p(|z|),thenf(z)is univalent inD,and the result is sharp.
Proof.Let


A tedious calculation yields (2.1) from the differential equation (1.4).
Let

Then, under the condition (ii), it is easy to see that

Combining (iii), we know that

This means that
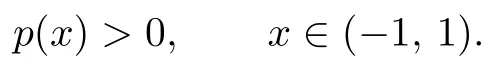
In addition, for x ∈(−1, 1), by Q(x, k)≠ 0 and (ii), it follows that p(x) is continuous for x ∈(−1, 1). Obviously, from (2.1), we can get that Q(x, k) is even for x ∈(−1, 1) implies that p(x) is even for x ∈(−1, 1). By (iii) again, according to Theorem 1.2, we know that f(z) is univalent in D.
Next, we prove the sharpness of the theorem.
For x ∈(−1, 1), by (ii) and Q(x, k)≠ 0, we have that there exists an M > 0 such that

Thus, combining

Note that p(x) is abstract in Theorem 2.1. The following results give some concrete p(x).
Theorem 2.2Let

where

Iff(z)is an analytic function inDsatisfying

thenf(z)is univalent inD.Moreover,the result is sharp.
Proof.Let

Then Q(x, k) satisfies the conditions (i) and (ii) of Theorem 2.1. Thus, applying (2.1), we can get (2.2). A straightforward calculation gives

Using x2= t, then (2.4) is equivalent to the following

it follows

Let

In order to apply Theorem 2.1, we firstly show that


When k≠ 0, note that
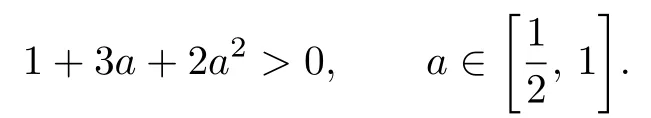
According to the graph of equation (2.5), if 0 < k < 1, then the symmetric axis t => 1 of the graph of equation (2.5). Obviously,

means that (2.6) holds. It follows

If k < 0, then the symmetric axis t =< 0 of the graph of equation (2.5), and

means that (2.6) holds. It follows

Thus, we obtain (2.3) from above analysis.
Next, we need to prove p(z) is self majorant.
In fact, it is obvious from the proof of Example 2.1. This completes the proof of theorem.
Remark 2.1According to Theorem 2.2, when a = 1, we can get that

Thus Theorem 2.2 reduces to Theorem 1 of [10].
Example 2.1Let

Proof.We rewrite (2.2) as

According to the conditions, whenand, we have


This means that all Taylor coefficients of p(z) are positive. Thus,

and the rest follows from Theorem 2.2.
Although the following result is also obtained by using Theorem 2.1, here we do not consider its sharpness.
Theorem 2.3Let

where.Iff(z)is an analytic function inDsatisfying|Sf(z)| 2p(|z|),thenf(z)is univalent inD.
Proof.Choosing Q(x, k) = (2 + x2)k, we can obtain (2.7) easily from (2.1). Let x2= t.Then a direct computation gives

it follows that

Let
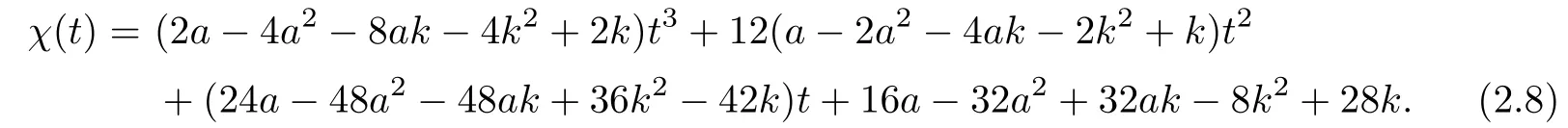
Applying Theorem 2.1, we have to prove that

We first consider the following three necessary conditions:

It follows that

From (2.8), we calculate

Using (2.9) and (2.10), if χ(t) is convex in t ∈(0, 1), i.e., χ′′(t) 0, then it is enough to see that

To make χ(t) convex. Now we only need

which is equivalent to

In view of (2.11), we conclude that

This completes the proof of theorem.
Remark 2.2We add another parameter to Q(x, k), i.e., we consider L(x, A, B), where A, B are positive parameters. If we write

where A > 0, in specially, let k =, then it is equivalent to the case of Theorem 2.2.Moreover, if we let

then it is Theorem 2.1 of [16] when A = 1. While, in Theorem 2.3 we consider another case when A = 2. In fact, it is interesting to consider the cases for fixing every A > 0.
 Communications in Mathematical Research2019年4期
Communications in Mathematical Research2019年4期
- Communications in Mathematical Research的其它文章
- Exact Solutions to the Bidirectional SK-Ramani Equation
- Global and Bifurcation Analysis of an HIV Pathogenesis Model with Saturated Reverse Function
- Global Existence and Blow-up for a Two-dimensional Attraction-repulsion Chemotaxis System
- Expanders, Group Extensions, Hadamard Manifolds and Certain Banach Spaces
- The Existence of Weak Solutions of a Higher Order Nonlinear Eilliptic Equation
- A Note on the Stability of K-g-frames
