基于B样条的支持向量分位数回归

杨联强，蔺一鸣，唐燕武

（1.安徽大学数学科学学院，安徽合肥230601；2.安庆师范大学数学与计算科学学院，安徽安庆246133）

支持向量机（SVM）首先由Vapnik[1]及其团队在AT&T Bell实验室提出，作为数据分析中分类和回归的强有力工具，其拥有优良的特性及完善的理论和算法[2-3]，因而得到广泛应用。相比于均值回归，分位数回归受异常值的影响较小而具有很好的稳健性，且能更完整地描述随机变量的分布特征，因此被回归分析普遍采用[4]。特别地，近几年学者们对支持向量分位数回归做了很多工作，综合了两者的优势特征，使之成为非常流行的回归分析工具[5-8]；同时更新的支持向量分位数回归方面的研究也得到进一步发展[9-10]。B样条最初由Schoenberg[11]提出，其分片多项式的构造、保持一定的连续性等性质使其拟合性能优越，后又由de-Boor给出著名的递推定义，使其计算快捷简单，从而成为数值分析、计算机图形学、函数逼近等领域强大的基本工具[12]。分位数回归的本质是对分位数函数的拟合，目前大多数用于分位数回归的基函数是各种核函数，例如高斯核函数、径向基核函数等，却少见将B样条用于分位数回归的研究。本文将B样条基函数用于支持向量分位数回归中，首先给出基于B样条的支持向量分位数回归模型，然后通过转化为对偶问题给出模型的求解过程，最后给出模拟和实际应用结果。

1 基于B样条的支持向量分位数回归

设(X1,Y1),(X2,Y2),…,(Xn,Yn)是来自二元总体(X,Y )的一组样本且X ∈[a,b]。 选取节点a=t1＜t2＜…＜tk= b 来构造次数为p 的B 样条基函数，则用作回归的基函数有k+p-1 个[12]，记B(Xi)=(B1(Xi),B2(Xi),…,Bk+p-1(Xi))T。设qτ(Xi)=WTB(Xi)是在给定Xi情况下Yi的τ(τ ∈(0,1))分位数，W 为系数向量，则基于B样条的支持向量分位数回归的目标函数定义如下：

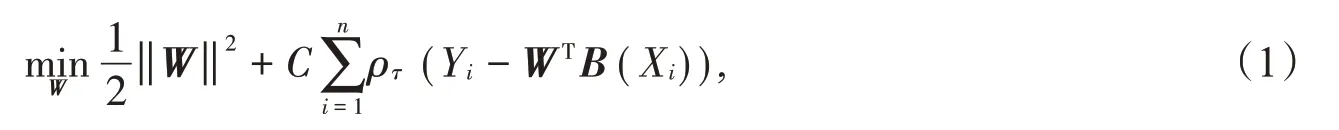
并使得Yi-WTB(Xi)≤ξi,WTB(Xi)-Yi≤ξ*i,ξi,ξ*i＞0，其中C是正则化参数，ρτ(r)为分pin-ball损失函数，ρτ(r)=(τ-1)rI(r ≤0)+τrI(r ＞0)。

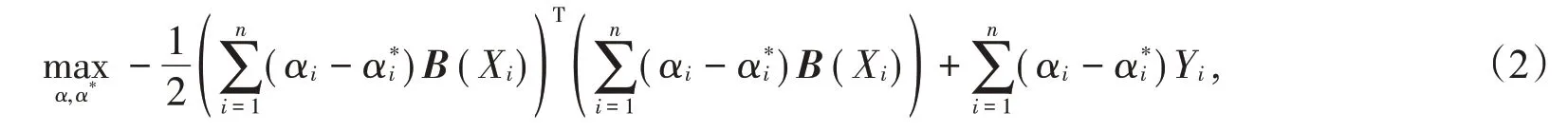
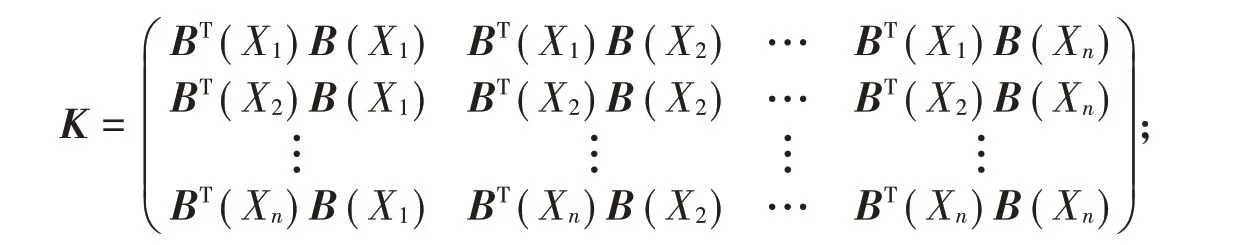
再通过R中的命令ipop(D,H,A,b,I,u,r)求解(2)式中则估计的分位数为

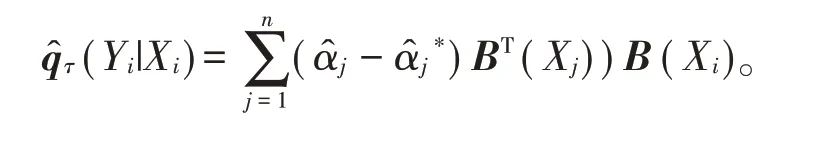
2 模 拟

通过两个模拟来展示B样条支持向量分位数的拟合效果。因为B样条能通过节点来局部控制函数形状，所以选取的两个模拟一个函数较为波动，另一个较为光滑。对于较为波动的函数，需用更多的节点来达到局部控制的效果，而较为光滑的函数则需要用较少的节点即能达到光滑的作用。两个模拟中的样条次数均为3。

例1设Y =e-7.5Xcos，其中X 在[0,1]区间上等间隔选取100 个样本点，数据如图1(a)所示。等间隔选取10个节点，并估计了在C=10,40两种情况下τ=0.05,0.25,0.5,0.75,0.95的分位数估计结果，如图1(b)，1(c)所示。

例2设Y =4X+sin+，其中X 在[0,2]区间上等间隔选取200 个样本点，数据如图2(a)所示。等间隔选取5个节点，估计了在C=5,10两种情况下τ=0.05,0.25,0.5,0.75,0.95的分位数估计结果，如图2(b)，2(c)所示。

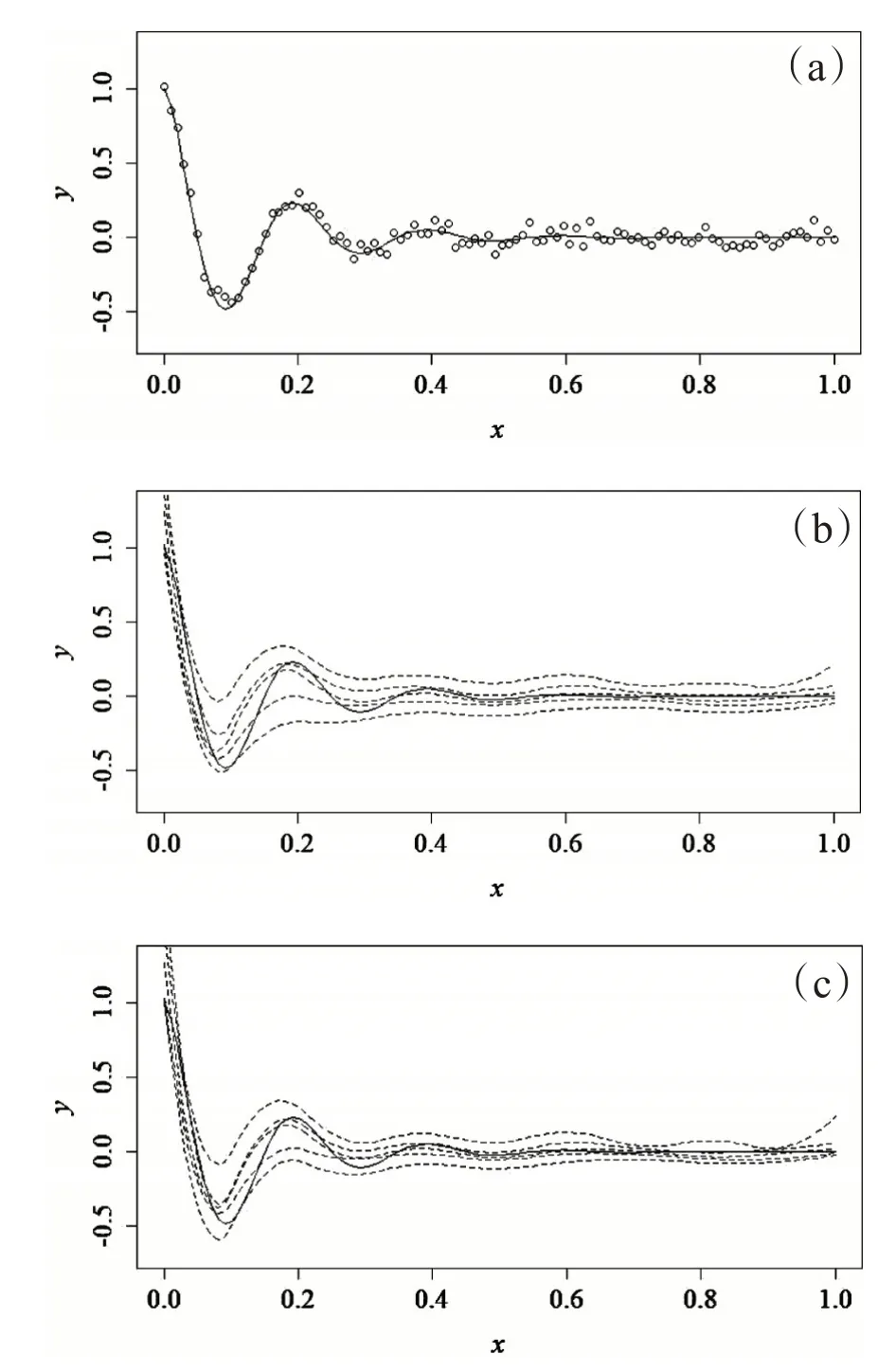
图1 例1真实函数（实线）、散点图及分位数估计（虚线）

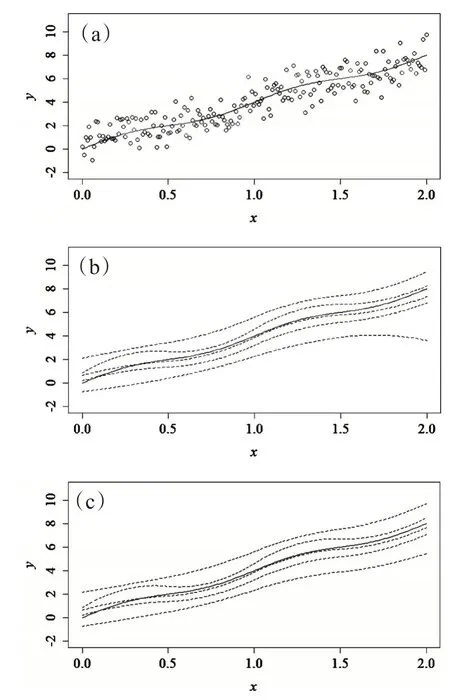
图2 例2真实函数（实线）、散点图及分位数估计（虚线）

3 应 用

选取R语言中cars包里的数据：1920年50组汽车速度（v/(km·h-1)）和刹车距离(s/m))的数据，通过B样条支持向量分位数回归对其进行分位数估计。因数据量较少且数据趋势较为光滑，所以这里等间隔选取3个节点来进行拟合，结果如图3所示。

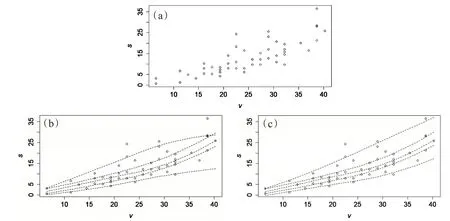
图3 （a）cars数据散点图；（b）、（c）分别为C=40，100时的0.05，0.25，0.5，0.75，0.95分位数估计

4 总 结

本文基于B样条，利用其拟合函数时表达能力强、可灵活调节等优点，将其作为支持向量分位数回归的基函数，构造了支持向量分位数回归模型。通过拉格朗日函数将模型求解的原始优化问题转化为对偶问题，再通过调用R中二次规划的程序包对其进行求解。模拟显示，本文方法给出的分位数估计表现良好，能比较完整地表示响应变量的条件分位数变化状况。但是，本文未系统讨论如何选取最优的调节参数，这是一个比较复杂的问题，涉及样条的次数、节点个数和位置以及惩罚参数的大小，这些理论工作有待进一步的研究。