2P-哈密尔顿二部连通图的能量条件

徐 弈，王礼想，舒阿秀

（安庆师范大学数学与计算科学学院，安徽安庆246133）

一个哈密尔顿图，是指包含一个过所有顶点的圈的图。如果图G中任意两顶点都有一条哈密尔顿路相连，则称G是哈密尔顿-连通的。如果平衡二部图G中不在同一分部中的任意一对顶点都有一条哈密尔顿路相连，则称G是哈密尔顿二部连通的。若一个平衡二部图G删除一个阶为2P的平衡子集后的子图是哈密尔顿二部连通的，则称G是2P-哈密尔顿二部连通的。由此可以看出，当p=0时，所表达的就是平衡二部图的哈密尔顿二部连通性。

图的哈密尔顿问题的研究一直是一个经典而又困难的问题，近年来研究这类问题的文献较多，而最近提出了一种新思想，即用能量刻画图的一些性质，亦取得了一些成果。如李饶在文献[1-2]中给出了用能量刻画无向简单图性质的一些条件；余桂东等在文献[3]中用带有最大度的能量刻画了无向简单图的哈密尔顿性。基于这些研究，本文用补图的能量给出了一个平衡二部图是2P-哈密尔顿二部连通的一个充分条件。

设G= ( )X,Y；E 是一个平衡二部图，它的k 闭包定义为将所有度和大于等于k 的顶点对(x,y)连接起来，其中x ∈X,y ∈Y，记为clk(G)。下面先介绍一些相关引理。

引理1[4]设P ≥0，G是一个2n阶平衡二部图。G是2P-哈密尔顿二部连通的当且仅当cln+p+2(G)是2P-哈密尔顿二部连通的。

引理2[5]设e是图G的任意一条边，则有左边等号成立当且仅当e是图G的一条孤立边，右边等号不成立。

引理3[6]设G 是一个n 阶图，有度序列d1≤d2≤···≤dn，则λ2(G)≥等号成立当且仅当G是正则图或者二部半正则图。

引理4[7]设G是一个二部图，则有λ(G)≤

定理1设G=是一个平衡二部图，满足=n ≥p+3。若

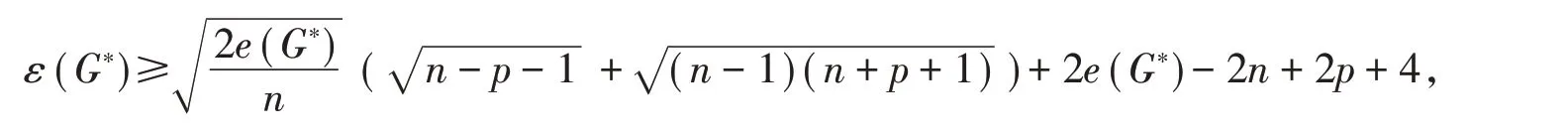
则G= ( X,Y；E )是2P-哈密尔顿二部连通的。

证明设G= ( X,Y；E )是一个满足定理条件的平衡二部图。如果G不是2P-哈密尔顿二部连通的，则由引理1，图H =cln+p+2(G)也不是2P-哈密尔顿二部连通的，因而，H不是完全二部图。由闭包的性质可知，H中任意一对不相连的顶点对(x,y)（其中x ∈X,y ∈Y）有dH(x)+dH(y)≤n+p+1。这意味在H的补图H*中，任意一对相连顶点对(u,v)都有dH*(u)+dH*(v)=n-dH(u)+n-dH(v)≥n-p-1，因而得出

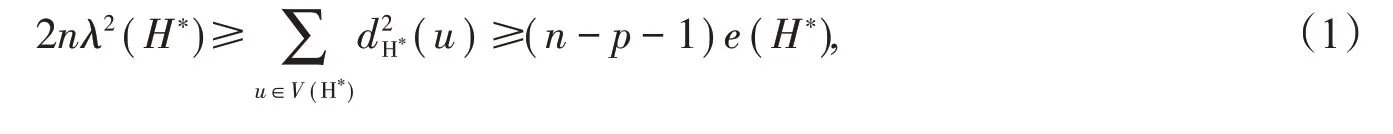
结合（1）式和引理4，可得

因为H*是平衡二部图，所以λ(H*)=-λ1(H*)。由图能量的定义和Cauchy-Schwartz不等式得

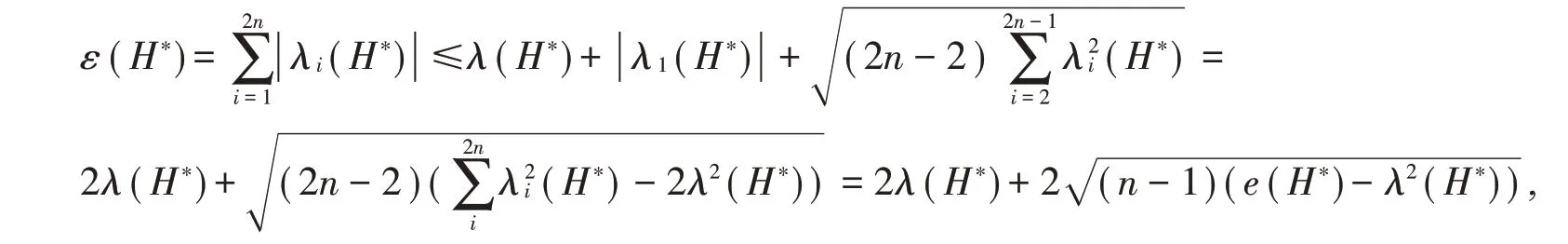
等号成立当且仅当λ2(H*)=···=λ2n-1(H*)。

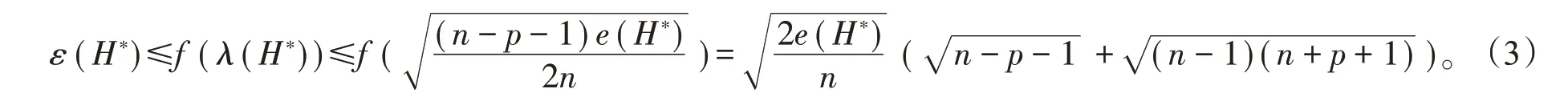
令s=e(G*)-e(H*)，因为H非空，所以至少有一对相邻顶点满足dH(x)+dH(y)≤n+p+1，则

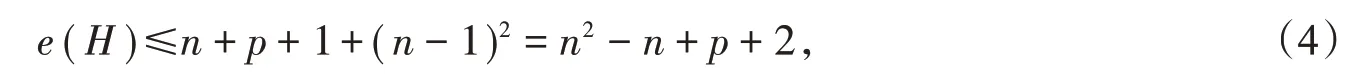
因 而s=e(G*)-e(H*)=e(H)-e(G)≤e(H)-(n2-e(G*))≤e(G*)-n+p+2。由 引 理2，可 以 找 到ε(H*)和ε(G*)之间的联系，即

又因为e(H*)≤e(G*)，代入（3）式可得

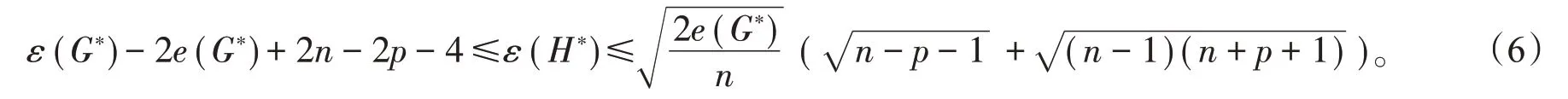
等式（1）成立当且仅当G 是正则图或者二部半正则图，等式（4）成立e(H)=n+p+1+(n-1)2，等式（5）成立当且仅当G有s条孤立边，相互矛盾，因而（1）、（2）、（4）、（5）式等号不能同时成立，所以（6）式等号取不到，因而

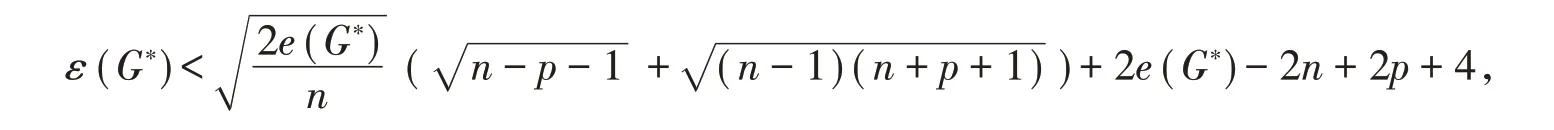
这与假设矛盾，因而定理成立。