基于子空间追踪的广义空间调制系统检测算法

杜力,张国华,刘文龙

(1.山西省交通规划勘察设计院,山西 太原 030012;2.山西省信息产业技术研究院有限公司,山西 太原 030012;3.大连理工大学 信息与通信工程学院,辽宁 大连 116024)

0 引言

空间调制(spatial modulation,SM)[1-4]是一种新的多输入多输出传输技术,该技术仅允许一根发射天线激活,并且利用天线的索引序号传输部分信息。这样不但避免了天线间同步以及天线间干扰的问题,还能够降低接收端信号检测的难度。为了进一步提高频谱效率,允许多根发送天线同时激活用于数据传输的广义空间调制(generalized spatial modulation,GSM)技术被提出[5-6]。

最大似然(Maximum-Likelihood,ML)检测算法通过穷尽搜索联合的激活天线索引以及激活天线发送的调制符号能够实现最优的检测性能。然而,该方法所需要的计算复杂度极高,导致其无法在实际中应用。针对这一情况,复杂度低的次优检测算法相继被提出。利用线性检测算法分别检测激活天线索引序号和激活天线发送的符号向量的方法被提出[6-8]。文献[9]中,一种复杂度低的球形译码检测算法被提出,该算法能够实现近似最优的性能,然而它的计算复杂度仍然太高,不适用于大规模GSM系统。在文献[10]中,针对大规模GSM系统,提出了一种分块排序最小均方误差检测算法能够实现近似最优的性能,并且相比于[9]中的检测算法计算复杂度有很大的降低。在文献[11]中提出了一种分层叠加编码的迭代检测算法能够实现接近ML检测的性能,并且计算复杂度降低81.25%。

此外,考虑到GSM信号的稀疏特性,压缩感知理论[12-14]已经被用于降低接收端信号检测的复杂度。文献[15]和[16]分别提出了一种稀疏重构检测算法和改进的压缩感知检测算法,能够以较低的复杂度获得较好的检测性能,充分体现了压缩感知理论在GSM系统检测中的应用前景。随后,基于压缩感知匹配追踪的SM匹配追踪检测算法[17]以及基于贝叶斯压缩感知的检测算法[18]被相继提出。在本文中,提出了一种基于压缩感知理论子空间追踪的检测算法。仿真结果表明, 所提出的检测算法较ML算法能够极大地降低计算复杂度, 并实现较好的检测性能。

1 系统模型

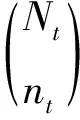
x(Ii,s)=[…,0,…si1,0,…,0,sint,0,…]T,

(1)

其中,(i1,…int)代表激活天线的索引序号。随后,发送信号通过空间信道进行传输到达接收天线。假设信道矩阵H∈Nr×Nt可以表示为:

(2)

其中,hi,j表示从第j根发送天线到第i根接收天线间的信道衰落系数。信道矩阵H中各元素相互独立,且服从均值为0,方差为1的复高斯分布。在接收端,接收信号向量y∈Nr×1可以表示为:

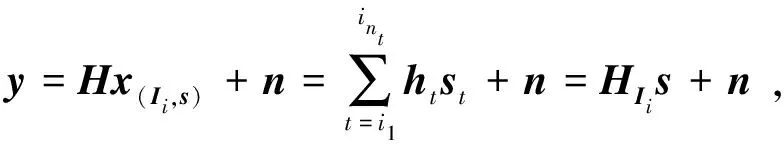
(3)

其中,HIi=(hi1,hi2,…,hint)是信号矩阵H包含nt列的子矩阵。s=(si1,…,sint)是激活天线的发送符号。n∈Nr×1高斯噪声向量,均值为0,方差为σ2。根据式(3),GSM-MIMO系统的ML检测算法可以表示为:

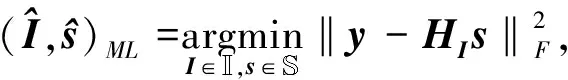
(4)

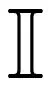
2 基于子空间追踪的检测算法

由式(1)可知,在GSM系统发送信号向量x(Ii,s)中,只有nt个非零元素,余下Nt-nt个元素都是0,且nt≪Nt,因此x(Ii,s)具有很强的稀疏特性。这使得将压缩感知理论用于求解GSM系统的检测问题成为可能。

压缩感知理论模型如下所示:

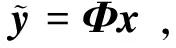
(5)

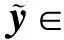
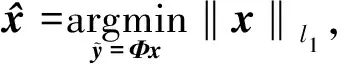
(6)

在GSM-MIMO系统的信道矩阵H刚好服从高斯分布,恰好满足RIP特性。这也是将压缩感知理论应用于GSM-MIMO系统中的一个重要的先决条件。在本文中,将压缩感知理论子空间追踪算法[19]的思想应用到GSM-MIMO系统的信号检测当中。子空间追踪算法的主要思想是:选出nt个合适的原子构成支撑集,然后利用回溯法去寻找比当前支撑集中更合适的原子,从而删除并且增加某些原子。整个迭代过程持续到前后两次迭代中,支撑集的原子不再发生变化。

首先,根据信道矩阵列向量与接收向量的内积,对天线索引进行第一次排序,如下所示:

[l11,l12,…,l1Nt]=argsort(|HHy|) ,

(7)

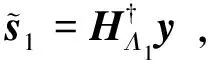
(8)

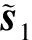
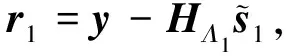
(9)

利用残差向量,得到一组新的天线索引序号,如下所示:

[l21,l22,…,l2Nt]=argsort(|HHr1|) ,

(10)

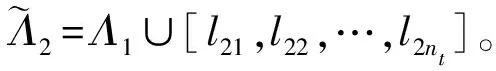
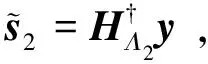
(11)

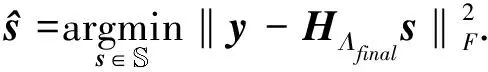
(12)

本文提出的算法主要复杂度集中在利用SP算法确定被激活天线索引,需要O(NtNrlognt) 的计算复杂度。随后,利用ML检测算法求解式(12),需要O(Mnt)的计算复杂度。因此,提出的算法最多需要O(NtNrlognt)+O(Mnt)的计算复杂度。

3 仿真结果及性能分析

为了验证本文提出算法的性能,采用matlab软件,在不同的调制方式和不同天线条件下对其进行仿真,并与ML、迫零(ZF, Zero forcing)、匹配滤波(MF, Matched filter)以及最小均方误差(MMSE, Minimum mean square error)等检测算法的误码率及算法运行时间进行比较。

3.1 仿真结果

图1给出了GSM-MIMO系统在数字调制方式采用BPSK的情况下,本文提出的SP-based算法与其他检测算法的误比特率(BER,Bit error ratio)性能比较。其中,图1(a)给出了Nt=10,Nr=10,nt=2场景下的BER性能曲线。图1(b)给出了Nt=50,Nr=20,nt=2场景下的BER性能曲线。如图1(a)所示,当天线规模较小时,提出的算法的BER性能与ZF算法及MMSE算法检测性能接近。由于提出算法对系统稀疏性有一定要求,因此,当天线规模较小时,提出算法的BER性能不能让人满意。如图1(b)所示,当天线规模较大,提出的检测算法的BER性能有明显提升。

图2给出了Nt=60,Nr=30,nt=2,数字调制方式采用4-QAM调制,提出算法与其他算法随信噪比变化的BER性能比较。如图2所示,提出的算法的BER性能优于其他算法,且随信噪比增加,BER性能有显著的提高。

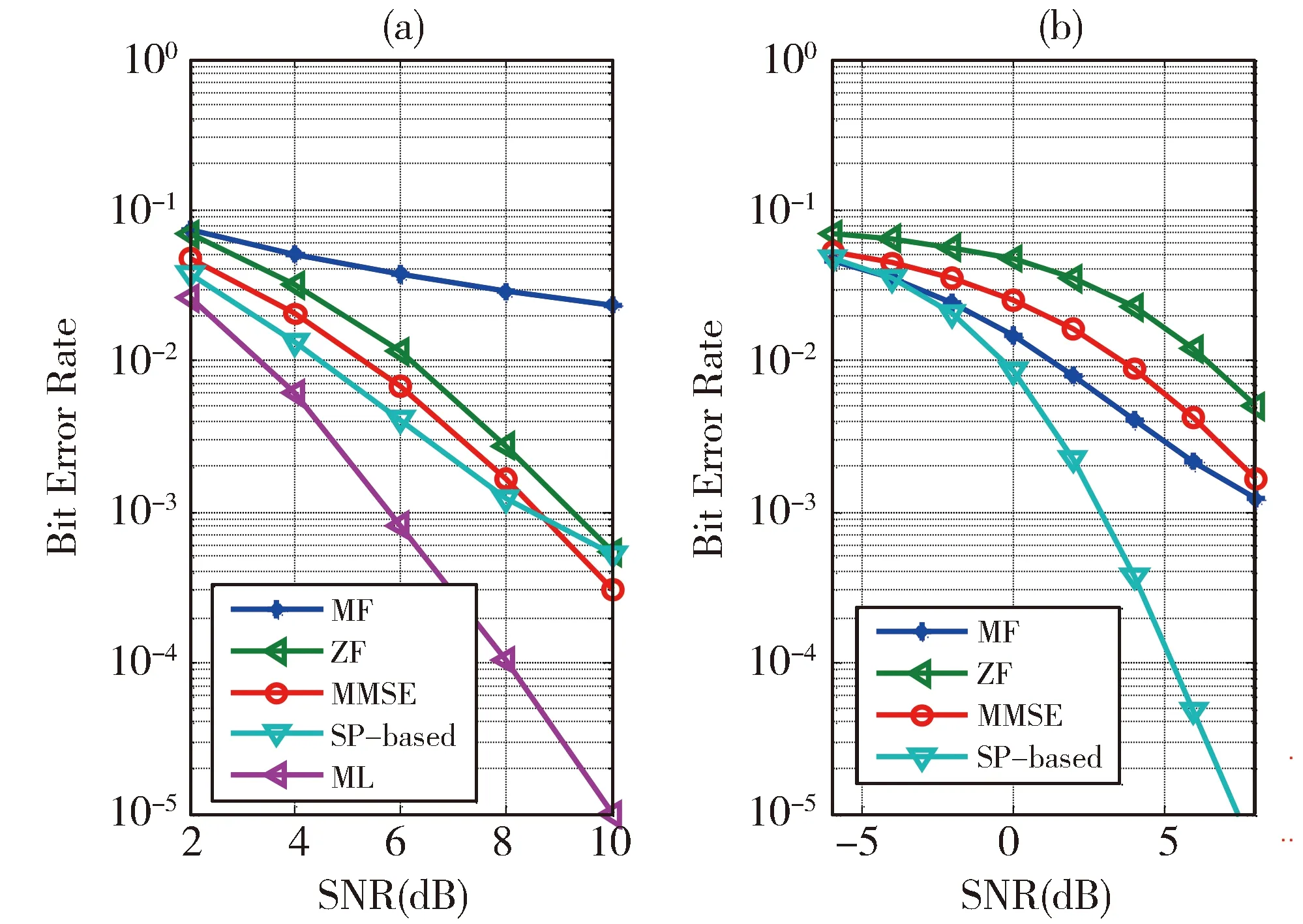
Fig.1 BER performance of SP-based and other detectors with BPSK modulation图1 BPSK调制下,SP-based算法与其他算法的BER性能

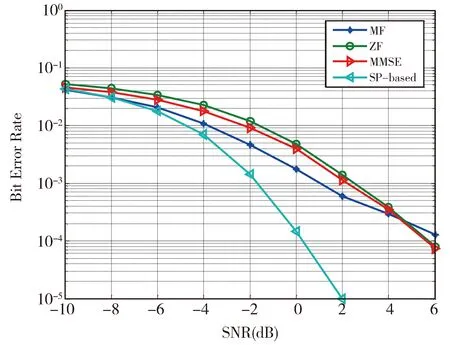
Fig.2 BER performance of SP-based and other detectors with 4-QAM modulation图2 4-QAM调制下,SP-based算法与其他算法的BER性能

表1给出了上述仿真实验所涉及算法在对应的3种仿真场景下的运行时间(运行10万次,单位:秒),其中实验1对应图1(a)的仿真场景,实验2对应图1(b)的仿真场景,实验3对应图2的仿真场景。如表1所示,提出算法运算复杂度多数情况下低于ML检测算法,ZF检测算法以及MMSE检测算法。

表1 三种实验场景下, SP-based算法与其他算法需运行时间(运行10万次)(s)

4 结论

针对ML检测在GSM-MIMO系统中计算复杂度过高的问题。本文提出了一种低复杂的基于子空间追踪的(SP-based)检测算法。该算法考虑GSM信号的稀疏特性,将压缩感知理论中子空间追踪算法回溯校验的思想应用于GSM-MIMO系统的信号检测。仿真实验证明了提出的算法的性能。