基于重叠网络的传染病动力学模型及分析

刘桂荣,韩立钦

(山西大学 数学科学学院,山西 太原 030006)

0 引言

近年来,复杂网络上的传染病动力学研究已越来越多,对疾病的预防和控制做出了很大的贡献,见文献[1-15]。然而，这些成果大部分是基于单层网络。事实上，两种疾病在同一群体内传播,一种疾病的传播会影响另外一种疾病的传播，如HIV能提高肺结核的发病率，这时用重叠网络来刻画更加符合实际。

文[16]在重叠网络上考虑了两种传染病的传播动力学，并假设一种疾病会影响所有个体对另一种疾病的感染率，进而建立了两个基于节点的不耦合的马尔可夫方程。利用矩阵特征值理论获得了两种疾病的传播阈值。理论结果表明，一种疾病的传播会影响另外一种疾病的传播阈值。显然，文[16]的建模机理是不合理的。事实上，只有当一个个体感染上一种疾病时，才会影响该个体对另外一种疾病的感染率。反之，如果一个个体没有感染上一种疾病，就不会影响该个体对另外一种疾病的传染率。

基于这个背景，本文将建立一个基于重叠网络和节点的两个耦合的马尔可夫方程，并研究其传播阈值。

1 模型建立

考虑两种传染病在一个群体中的传播。如图1所示,根据第一种疾病的传播方式，将这个群体中的每一个个体看作一个节点,个体之间的接触看作连边，形成网络H1;同样地,根据第二种疾病的传播方式，形成网络H2。也就是，第一种疾病在网络H1中传播;第二种疾病在网络H2中传播。

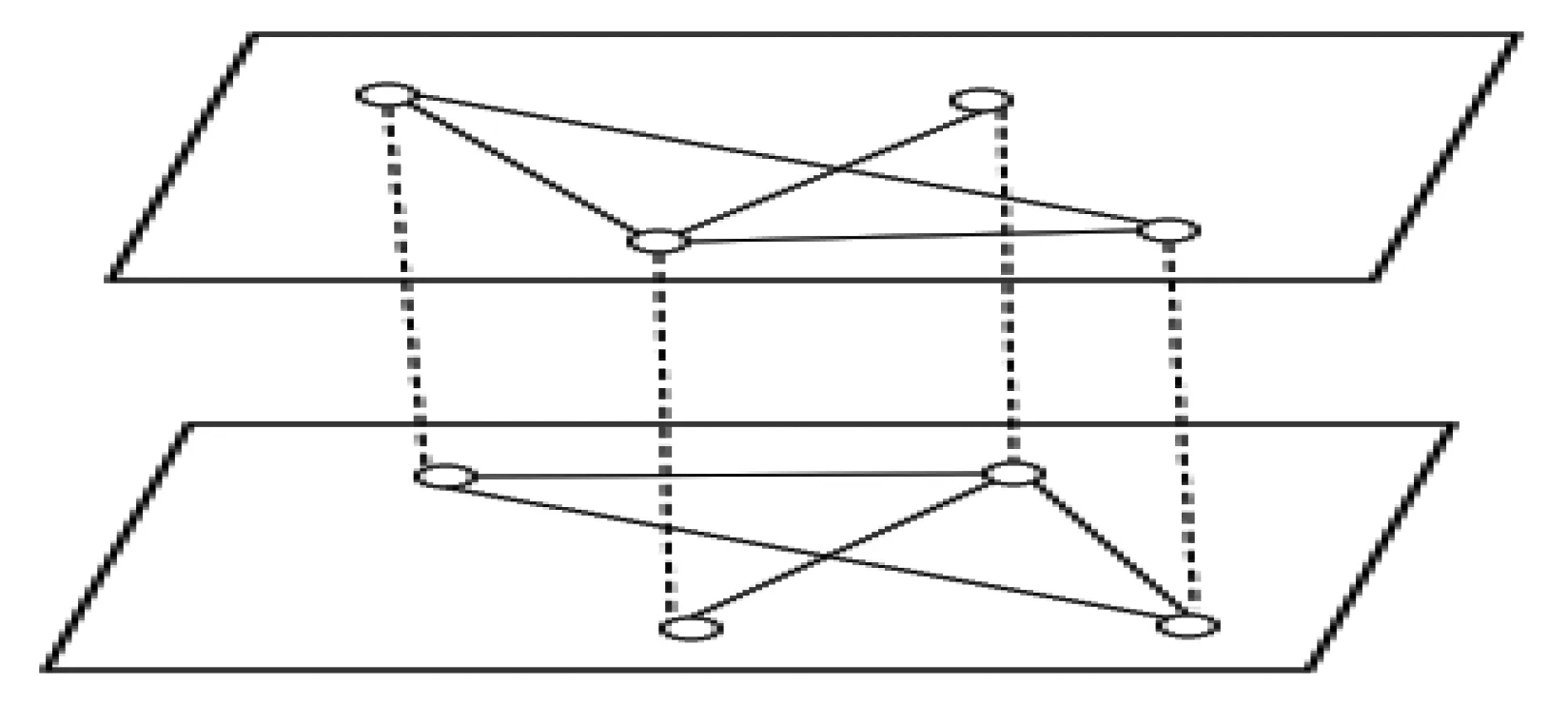
Fig.1 Overlapping network H1 and H2图1 重叠网络H1与H2

设重叠网络有N个节点。记网络H1,H2的邻接矩阵分别为A=(aij)N×N,B=(bij)N×N当网络中只有第一种疾病传播时,β1表示网络H1中染病节点传染易感节点的传染率,μ1表示H1中染病节点的恢复率。相似地，当网络中只有第二种疾病传播时，β2表示H2中染病节点传染易感节点的传染率;μ2表示H2中染病节点的恢复率。在重叠网络中，一层中一个易感节点的感染率会受到另一层中该节点染病状态的影响，k1>0为H1中一个易感节点的感染率受H2中该节点染病状态的影响系数;k2>0表示H2中一个易感节点的感染率受H1中该节点染病状态的影响系数。例如，如果在H1中的一个易感节点没有感染第二种疾病(或感染第二种疾病),那么当该节点在H1中与染病节点接触时，传染率为k1β1，其中k1=1(或k1≠1);如果在H2中的一个易感节点没有感染第一种疾病(或感染第一种疾病)，那么当该节点在H2中与染病节点接触时，传染率为k2β2,其中k2=1(或k2≠1)。此外，01表示第二种疾病促进第一种疾病的传播。关于k2的不同取值情形，有类似的解释，pk,i(t)(k=1,2)表示第k层网络中第i个节点在t时刻是染病者的概率。

根据上述传播机理,可建立基于节点的马尔可夫方程组:

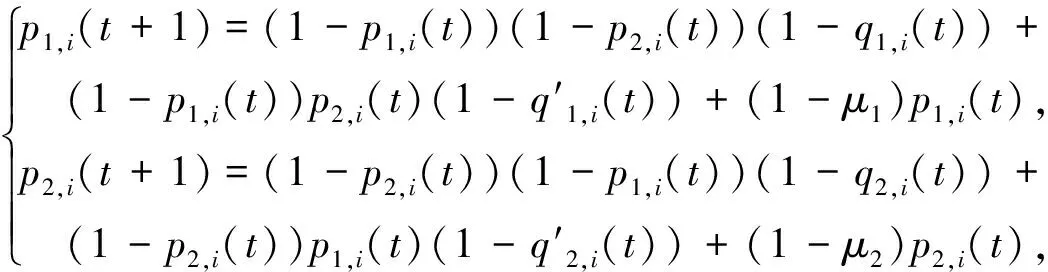
(1)

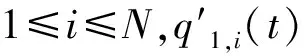
(2)

与

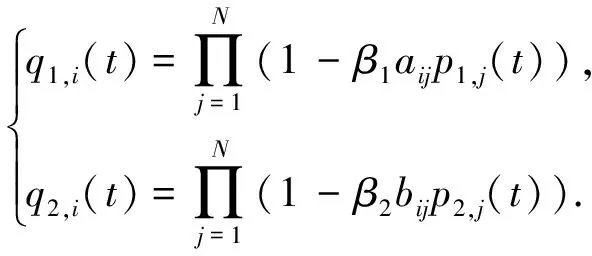
(3)

在(1)中,第一个式子右端的第一项表示t时刻，第i个节点在网络H1和H2中都是易感者时，该节点被H1中邻居感染的概率;第二项表示t时刻，第i个节点在网络H1中是易感者，在H2中是染病者时，该节点被H1中邻居感染的概率，第三项表示H1中第i个节点在t时刻为染病者且没有恢复的概率。(1)中第二个式子，有类似的解释。

由于系统最终会达到稳定状态,则网络H1中疾病与H2中疾病的最终感染率ρ1，ρ2分别为:

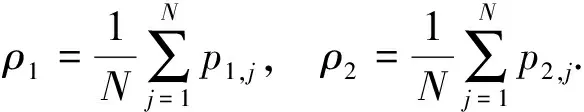
(4)

2 主要结果

为了研究(1)的平衡点, 考虑下列代数方程组

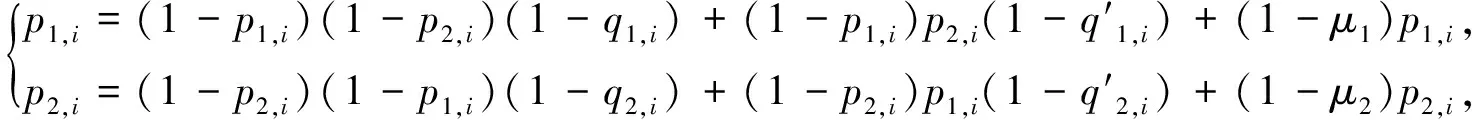
(5)

其中

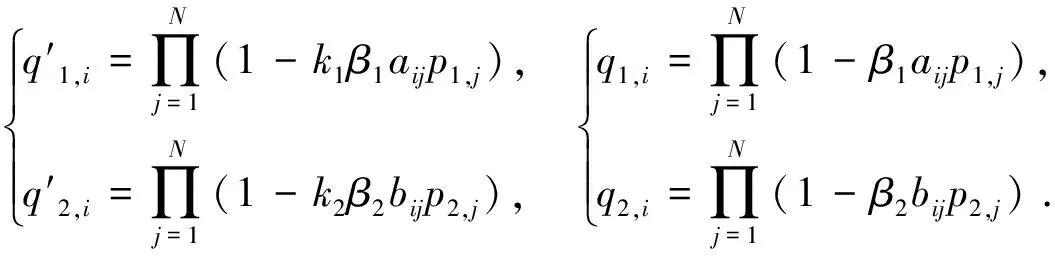
(6)

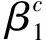
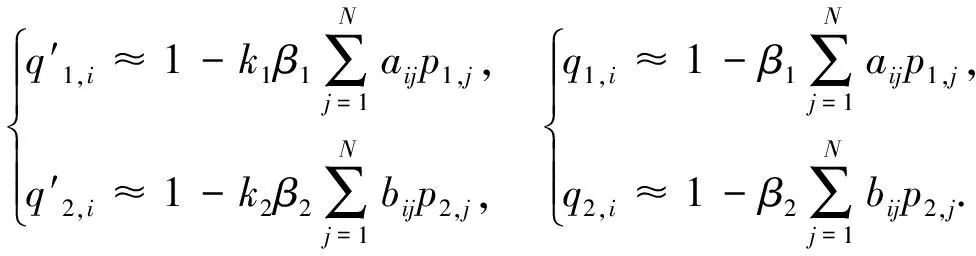
(7)

将(7)式代入(5)式, 忽略二次项可得:

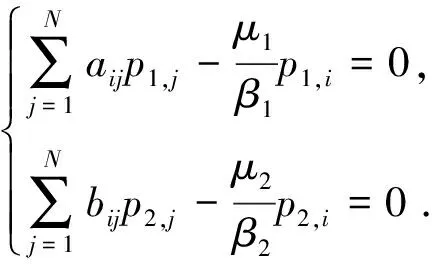
(8)

令P1=[p1,1,p1,2,…,p1,N]T,P2=[p2,1,p2,2,…,p2,N]T从而(8)式可以写成:

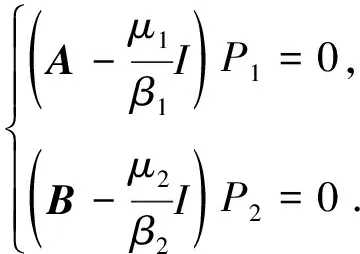
(9)

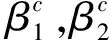
(10)

其中Λmax(A)代表邻接矩阵A的最大特征值,Λmax(B)代表邻接矩阵B的最大特征值。

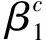
3 数值模拟

在数值模拟中,每层网络将分别由800个节点组成,且服从幂律分布,分布指数为2.5。我们将感染率初始值设为0.05,恢复率μ1=0.6,μ2=0.4.

令k1=4,k1=2.重叠网络中网络H1在不同k1的取值下,最终感染率ρ1随传染率β1变化对比图,见图2。

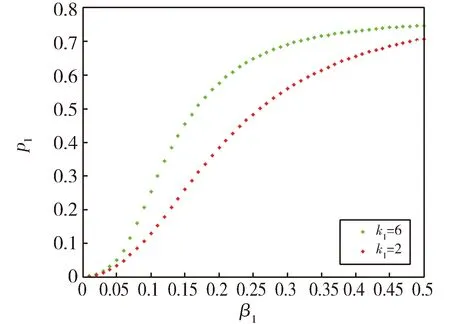
Fig.2 Diagram of ρ1 with β1 in H1图2 网络H1中,ρ1随β1变化的对比图

令k2=0.6,k2=0.4.重叠网络中网络H2在不同k2的取值下,最终感染率ρ2随传染率β2变化对比图,见图3。

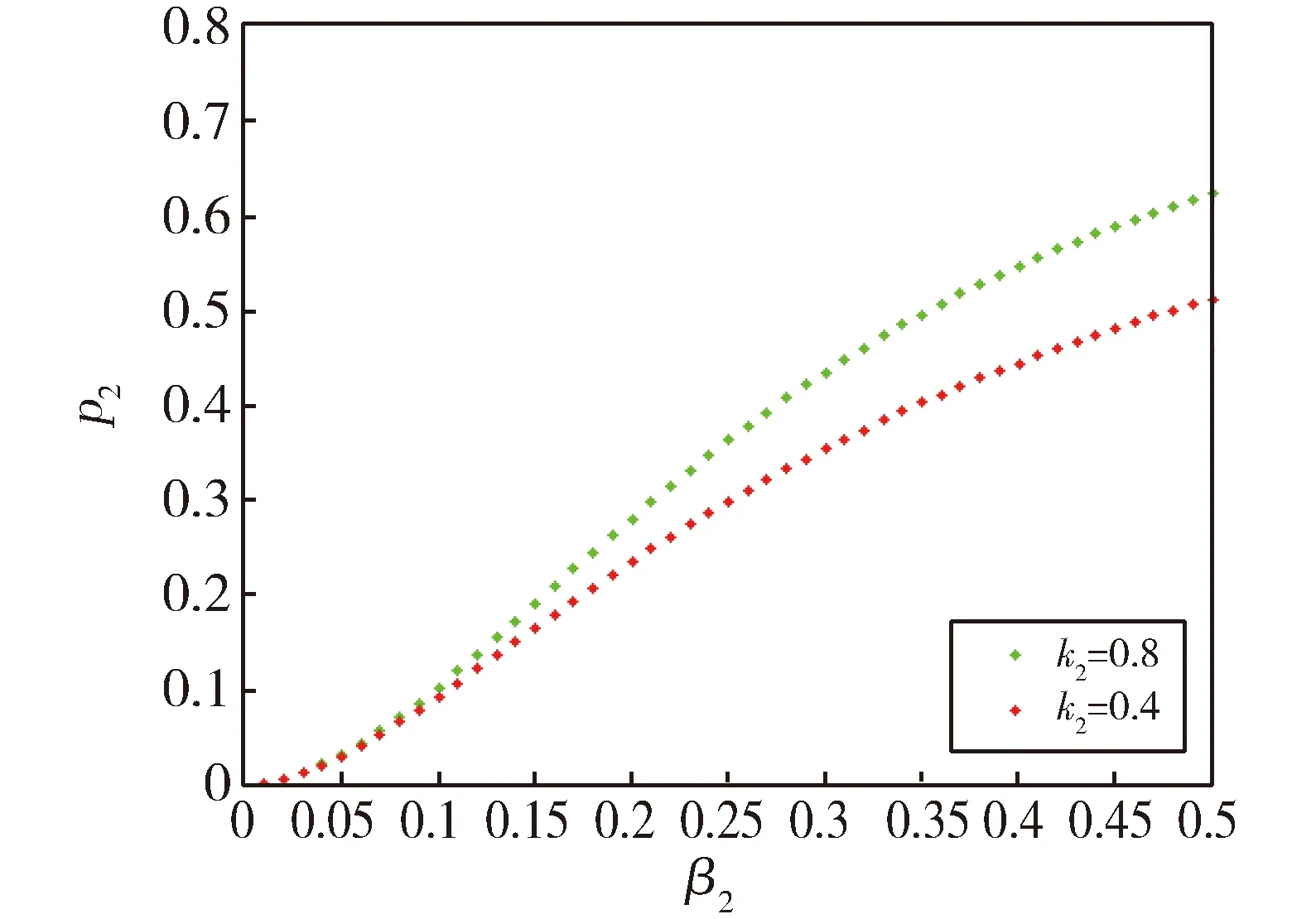
Fig.3 Diagram of ρ2 with β2 in H2图3 网络H2中,ρ2随β2变化的对比图

从图2和图3的数值模拟结果可以看出,虽然ki(i=1,2)的取值不同，但两种疾病的传播阈值是相同的。此外，随着ki(i=1,2)的增大,网络的最终感染率ρi(i=1,2)也随之增大。进而,一种疾病的传播会影响另外一种疾病的染病规模。