高速铁路多节拍组合运行图优化模型与算法
周文梁,姜 敏,薛利娟
中南大学交通运输工程学院,湖南长沙 410075
节拍式列车运行图具有规律性强、使用灵活及方便旅客出行与车站工作组织等优点,在日本、欧洲的一些国家得到广泛应用.PEETERS[1]提出周期事件规划问题(periodic event scheduling problem,PESP)模型和周期性列车运行图编制(cycle periodicity formulation,CPF)模型;CAIMI等[2]在此基础上提出周期运行图的弹性PESP模型;汪波等[3-4]借助网络约束图及周期势差模型,以列车停站时间最少为目标,建立城际铁路与城轨周期运行图优化方法;谢美全等[5]考虑列车周期性运行约束,建立基于定序的周期性运行图优化方法;贾晓秋等[6]构建了高速铁路周期列车运行图的多目标模型,并设计基于job-shop的遗传算法;李传宾[7]基于矩阵表示和极大代数法设计高速铁路(即高铁)周期列车运行图优化方法.
周期列车运行图虽能提供旅客规律化的运行列车以方便旅客出行,然而在其编制过程中,通常是基于高峰期出行需求确定该时段列车时刻表,通过进一步复制和删除非高峰时段部分列车而获得全天列车运行图.如此一来,列车原本严格的等时间间隔周期运行规律将在一定程度上被破坏.为使列车运行具有严格的等间隔运行规律,能够使不同时段列车运行数量与出行需求量相适应,本研究基于列车多节拍协同运行方式,将具有相同起点、终点、停站方案以及速度等级的列车归为一个节拍单元.同节拍单元列车以严格的等时间间隔周期运行,而不同节拍单元列车可具有不同的运行时间间隔,进而协调优化各节拍单元列车运行的时间间隔及其车站到达与出发时间,由此获得的列车时刻表,不仅具有严格的等时间间隔运行规律,还能使不同时段的列车运行数量与出行需求量相适应.
1 优化模型
考虑由K个车站与K-1个复线区间构成的高铁线路L=(S,E)上多节拍单元列车运行图优化问题,其中,S为线路车站序列;E为线路区间集.为简便起见,该问题研究基于以下假设.
假设1车站简化为具有停车能力属性的节点,不考虑列车在车站运行路径,但要求车站同一时间内的停留列车数量不能超过该站停车能力.
假设2线路仅运营多个节拍式运行列车,不包含非节拍运行列车.
假设3同节拍单元列车采用相同的车底或动车组,所有同节拍列车具有相同定员.
这种多节拍组合运行方式能够使得各节拍单元列车严格按某固定时间间隔周期性运行,以方便旅客乘车出行,而且能够通过协调各节拍单元首列车始发时刻及其运行时间间隔,使得客流高峰期组织运行更多列车,而在客流低峰期运行少量列车以适应不同时期客流需求的变化.
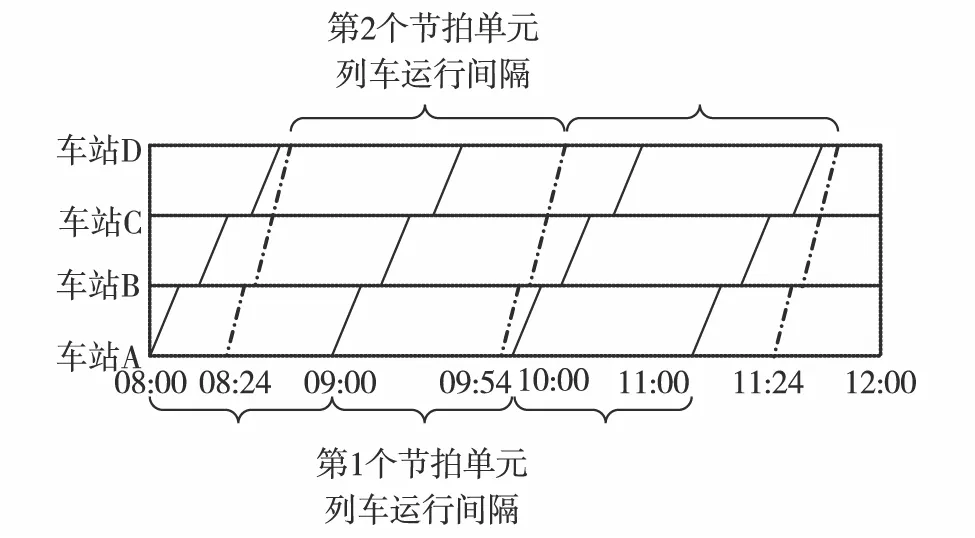
图1 由2个运行节拍单元构成的列车运行图Fig.1 A train schedule with two period-types of trains
多节拍单元列车运行图优化旨在优化各节拍单元列车运行时间间隔、以及各节拍单元列车在车站的到达与出发时刻,使其在满足各类运营与行车时间标准条件下,所有节拍单元列车总旅行时间达到最小.该优化问题所涉及到的相关参数符号定义如表1,决策变量与辅助变量的定义如表2.
以最小化所有节拍单元列车旅行时间之和为目标,实现多节拍列车组合运行时刻表优化,其具体模型为
(1)
该模型满足以下7组约束条件:
1)同节拍单元列车等间隔运行约束.
aw, f+1(i,j)=aw, f(i,j)+Tw, ∀w;f=1,2,…,mw-1; (i,j)∈Ew
(2)

表1 符号定义
dw, f+1(i,j)=dw, f(i,j)+Tw,∀w;
f=1,2,…,(mw-1); (i,j)∈Ew
(3)
约束式(2)和(3)确保节拍单元w两相邻列车的到达(出发)时刻的时间间隔长度为Tw.
2)列车发车达到最低客座率约束.
(4)

表2 决策变量与辅助变量的符号定义
aw, f+1(rw,j)-aw, f(rw,j)≥RTw(aw, f(rw,j)),
∀w;f=1,2,…,mw-1; (rw,j)∈Ew
(5)
3)区间运行时分标准与最小停站时间约束.
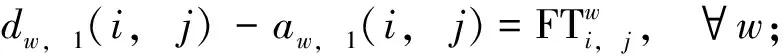
(i,j)∈Ew
(6)
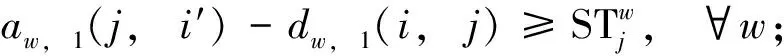
(i,j),(j,i′)∈Ew
(7)
约束式(6)与(7)分别确保节拍单元w首列列车区间运行时间与车站停站时间分别不低于其相应的最小值.
4)列车间最小安全到达与出发时间间隔约束.
aw′, f′(i,j)+ATi, j,
∀[w,f]≠[w′,f′]; (i,j)∈Ew∩Ew′
(8)
dw′, f′(i,j)+DTi, j,
∀[w,f]≠[w′,f′]; (i,j)∈Ew∩Ew′
(9)
约束式(8)保证节拍单元w第f列列车与节拍单元w′第f′列列车进入区间(i,j)的时间间隔不小于最小安全间隔ATi, j,离开区间(i,j)的时间间隔不小于最小安全间隔DTi, j.
同理,约束式(9)确保节拍单元w第f列列车与节拍单元w′第f′列列车离开区间的时间间隔不小于最小安全间隔DTi, j.
5)车站最大同时停留列车数约束,即车站停车能力约束.
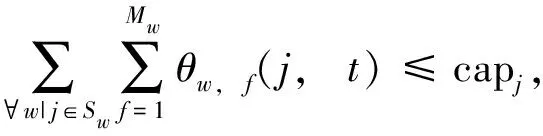
∀j∈S;t=1,2,…,T
(10)
约束式(10)保证了车站j在任意时刻t停留的列车总数不会超过其停车能力capj.
6)列车到发时间取值范围约束.
1≤aw,f(i,j)≤T, ∀w;
f=1,2,…,mw; (i,j)∈Ew
(11)
1≤dw,f(i,j)≤T, ∀w;
f=1,2,…,mw; (i,j)∈Ew
(12)
约束式(11)和(12)分别使得列车进入和离开区间的时间均在列车运营时间1~T以内.
7)决策变量间一致性约束.
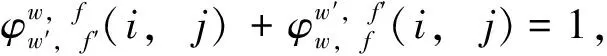
∀[w,f]≠[w′,f′]; (i,j)∈Ew∩Ew′
(13)
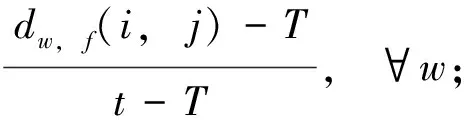
f=1,2,…,mw;t=1,2,…,T; (i,j)∈Ew
(14)
[1-ρw, f(i,j,t)]×M,∀w;
f=1,2,…,mw;t=1,2,…,T;
(i,j),(j,i′)∈Ew
(15)
θw, f(j,t)≤ρw, f(i,j,t), ∀w;
f=1,2,…,mw;t=1,2,…,T; (i,j)∈Ew
(16)

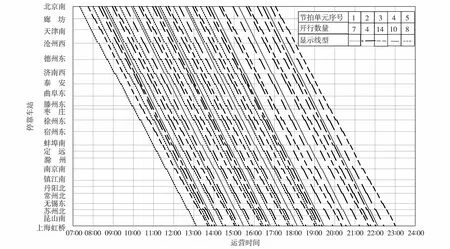
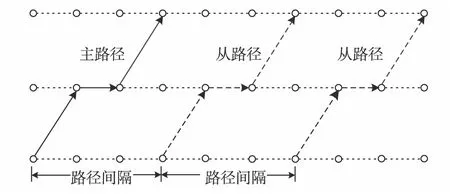
约束式(15)和(16)共同确保仅当列车[w,f]在车站j的到发时间满足dw, f(i,j)≤t 本节设计交叉元启发算法求解模型.首先,基于初始化的概率参数随机生成多个解编码,基于每个解编码采用多路径搜索算法生成一个多节拍运行时刻表;其次,衡量各个体解对应列车时刻表质量,按一定比例挑选其中的精英解;最后,根据挑选出来的精英解更新概率参数,并以此概率随机生成新的个体解编码.通过如此反复改进概率参数,使较高质量个体解编码能以更高概率生成,而较差质量个体解编码因其生成概率较低而逐将淘汰. 图2为解编码示意图,每个节拍单元包含优先权值、以整数表示的始发时刻与运行间隔3个基因位.其中,优先权值决定了节拍单元列车铺画的先后顺序;始发时刻与运行间隔分别确定了首列车发车时刻与运行时间间隔. 图2 解编码示意图Fig.2 The schematic diagram of solution encoding 每个节拍单元列车基因值通过离散概率分布函数生成.记αw,r,n为第n次迭代中节拍单元w列车选择优先权Qw=r的概率,此时,r=1,2,…,W;βw,r,n与γw,r,n分别为第n次迭代中节拍单元w列车选择始发时刻dw=t与运行时间间隔Tw=Δt的概率. 初始化时,各节拍单元列车基因所有取值的选择概率相同,然后基于精英解更新,使精英解中基因值能以较高概率进入后续个体解编码,具体方法(以参数βw,r,n为例,其他参数类似)为 (1-ρ)·βw,r,n-1 (17) 其中,GS为每次迭代种群中个体数量;σ为选择精英解的比例;ES为当前迭代选中的精英解集合;Tw(n,k)表示第n次迭代中第k个解中节拍单元w参数Tw的取值;参数ρ为权衡系数. 对每个节拍单元,定义其首列列车运行路径为主路径,其余列车运行路径为从路径,主路径与从路径起点时刻间隔称为路径间隔,如图3. 图3 节拍单元列车运行的主路径、从路径及路径间隔示意图Fig.3 Headways between primary path and subordinate path of a period-type 算法开始时,仅初始化所有备选起始节点的标号集,而其余节点标号在之后的路径搜索过程中根据需要添加.当搜索节拍单元w列车路径时,起始节点标号初始化如下 (18) tn+(mw-1)×Γ+Rw≤T (19) 其中, Rw表示节拍单元w列车按区间最小运行、车站最小停站时间运行所花费的总旅行时间. 接下来,算法需通过不断生成新标号,更新既有标号值搜索从起点到各节点总费用最少的主路径与间隔值,具体过程为 步骤1逐一选择标号集Bnew中标号,对于当前标号b, 根据其与前序标号的对应车站及停站时间,更新其后续节点标号如下: 步骤2令Bnew=Bupdate, 从Bupdate中选择标号值最小的标号b*, 令ηb*=1、Bupdate=Ø. 若标号对应节点车站为列车终点站,则停止算法计算;否则,重复以上步骤更新节点标号. 在以上路径搜索中,为避免当前节拍单元列车路径与已确定列车路径产生作业冲突,任何搜索到的主路径与从路径均不可包含:① 之前已确定节拍单元列车路径所含有向弧;② 若被使用将与第1类有向弧违背最小安全到达时间间隔或最小安全出发时间间隔约束的有向弧. 算法一旦满足以下任一条件便终止迭代. 1)对任意节拍单元列车,βw,r,n与γw,r,n>(1-ω)或<ω. 同样,εw,r,n与εw,r,n>(1-ω)或<ω, 其中,ω为一很小正数值, 通常取ω=0.01; 2)从算法开始所获得的最优个体解对应的目标函数值连续μ次迭代未发生改进; 3)当前迭代次数达到给定最大迭代次数nmax. 考虑由6个车站、5个复线区间线路,运营时间为[1,180] min,且各区间最小安全出发、到达间隔为3 min.所有列车均从线路端点站出发到达另一端点站,停车随机确定,且最小停车时间为1 min. 图4 算法计算时间CT与Gap随节拍单元数量的变化关系Fig.4 The change relation of CT and Gap with the number of period-types 图4(a)与(b)分别给出当节拍单元平均列车数为3~7列时,算法计算时间(CT)与目标函数与最优值相对差距(Gap)随节拍数量增加的变化.显然,CT呈先慢后快增长趋势.如在平均列车数为4时,节拍单元数量从2增至4,计算时间增幅较小,但之后却大幅增加.另外,节拍单元平均列车数越少,计算时间增速反而较大,主要原因是在平均列车数量较少时,每个节拍单元列车可搜索的路径范围与时间间隔值均较多,导致更多的计算时间.由图4(b)可知,随节拍单元数量增加,算法基本能搜索到最优解,仅在平均列车数为7列、节拍单元为4时,没有搜索到最优解,此时Gap约为10%. 图5 算法计算时间CT与Gap随节拍单元平均列车的变化关系Fig.5 The change relation of CT and Gap with the increase of average train number of period-types 图5(a)与(b)分别给出不同节拍单元数量时,CT与Gap随着节拍单元平均列车数增加的变化关系.由图5(a)可知,随着节拍单元平均列车数量的增加,CT反而下降.主要原因是算法并不需要为同节拍单元列车逐列搜索路径,而只需寻找具有开行间隔属性的出行路径,反而节拍单元平均列车数越少,首列列车路径的搜索时间范围与对应的列车运行间隔范围越大,计算时间越多.由图5(b)可知,在节拍单元平均列车数较少时,Gap均为0,但当继续增加至6以后,Gap具有一定的波动性,最大值接近18.0%. 图6(a)与(b)分别给出当节拍单元平均列车数为3~6列时,CT与Gap随高、中速节拍单元数量之比增加的变化关系.由图6(a)可知,在节拍单元平均列车数为5列或6列时,高、中速节拍单元数量之比变化对计算时间影响较大,但当节拍单元平均列车数为3列或4列时,算法计算时间变化范围相对较小.由图6(b)可知,在节拍单元平均列车数较少时,Gap一直保持为0;而当节拍单元平均列车数为6列时,Gap达到最大值29.6%、最小值1.4%.由此可见,在节拍平均开行列车数量较少时,高、中速节拍单元列车混行对CT与Gap影响均较小;但当节拍平均列车数量较大时,将导致CT与Gap增加. 图6 算法计算时间CT与Gap随高、中速节拍单元数量比的变化关系Fig.6 The change relation of CT and Gap with the rate increase of high-speed to middle-speed period-type 以京沪高铁线路为例,仅考虑北京南至上海虹桥的节拍列车,暂不考虑其他非节拍列车.假定共有5个节拍单元列车,其列车数量及停站序列见表3,运营时间为07∶00—24∶00,且在各区间的最小安全出发、到达时间间隔分别为5 min和6 min. 表3 各运行节拍单元列车停站序列以及运行数量Table 3 The number of trains and stop sequences of each period-type train 为方便记忆列车运行时刻,以10 min的整倍数作为列车运行时间间隔的可能取值.经4.31 h的计算后,获得列车运行图如图7,此时,Gap为6.8%. 由图7可知,每个节拍单元列车均按所确定的时间间隔等间隔运行,通过协调各节拍单元列车最早发车时间与时间间隔使得全天不同时段具有不同数量的列车,以满足不同时段旅客需求.经比较发现,具有较多数量列车节拍单元的运行时间间隔相对较小,反之相对较大,从而使列车尽可能分散到全天运营时间范围内,避免列车集中运行. 本研究以最小化列车总旅行时间为目标,构建多节拍单元列车协同运行时刻表优化模型.在定义主路径、从路径及路径间隔等概念的基础上,将交互熵原理与多路径组合搜索算法相结合,设计了时刻表优化的元启发式算法. 本模型与算法暂未考虑客流因素,今后研究需进一步将客流因素反映到模型与算法中.此外,关于车站到发数量、车站路径选择限制的考虑、以及将本方法推广到小规模轨道网络同样是需要进一步研究的内容. 图7 07∶00—24∶00以10 min的整数倍为运行间隔的多节拍列车运行图Fig.7 The multi-periodic train timetable based on setting train operation period as the integer multiples of 10 min during 07∶00 to 24∶002 算法设计
2.1 解编码及其生成法

2.2 基于给定解编码的多节拍列车时刻表生成算法
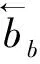
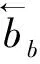
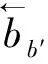
2.3 算法终止条件
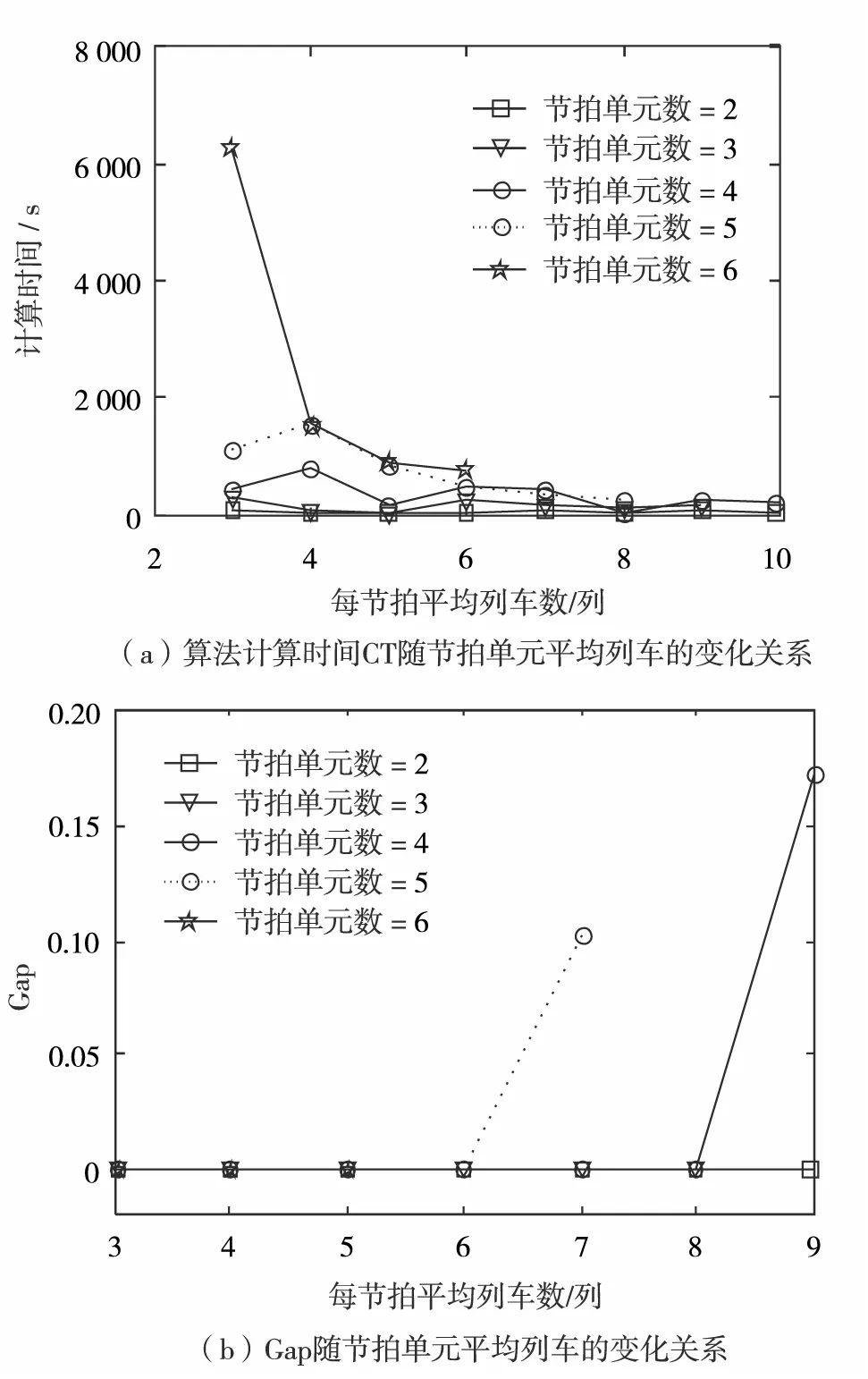
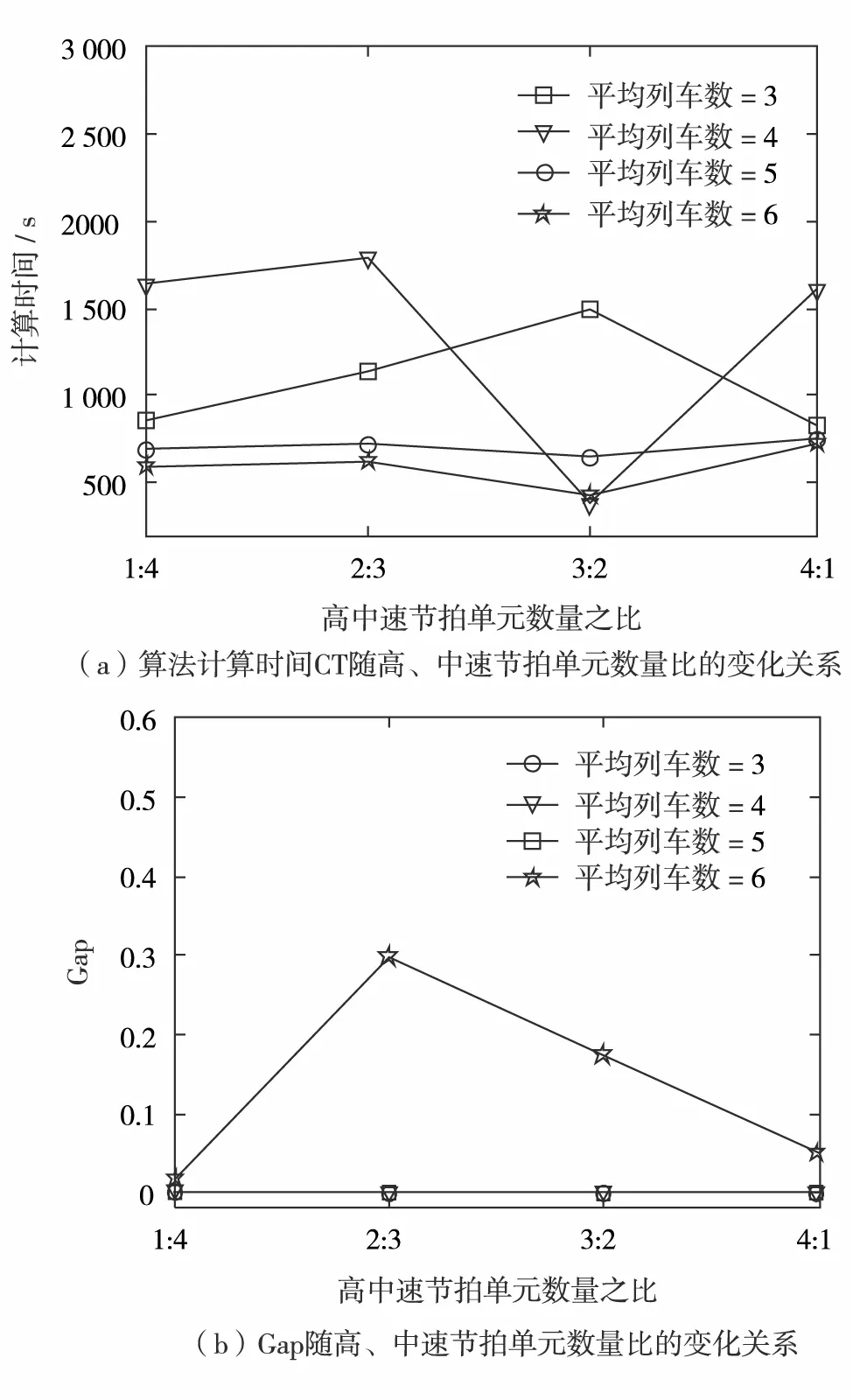
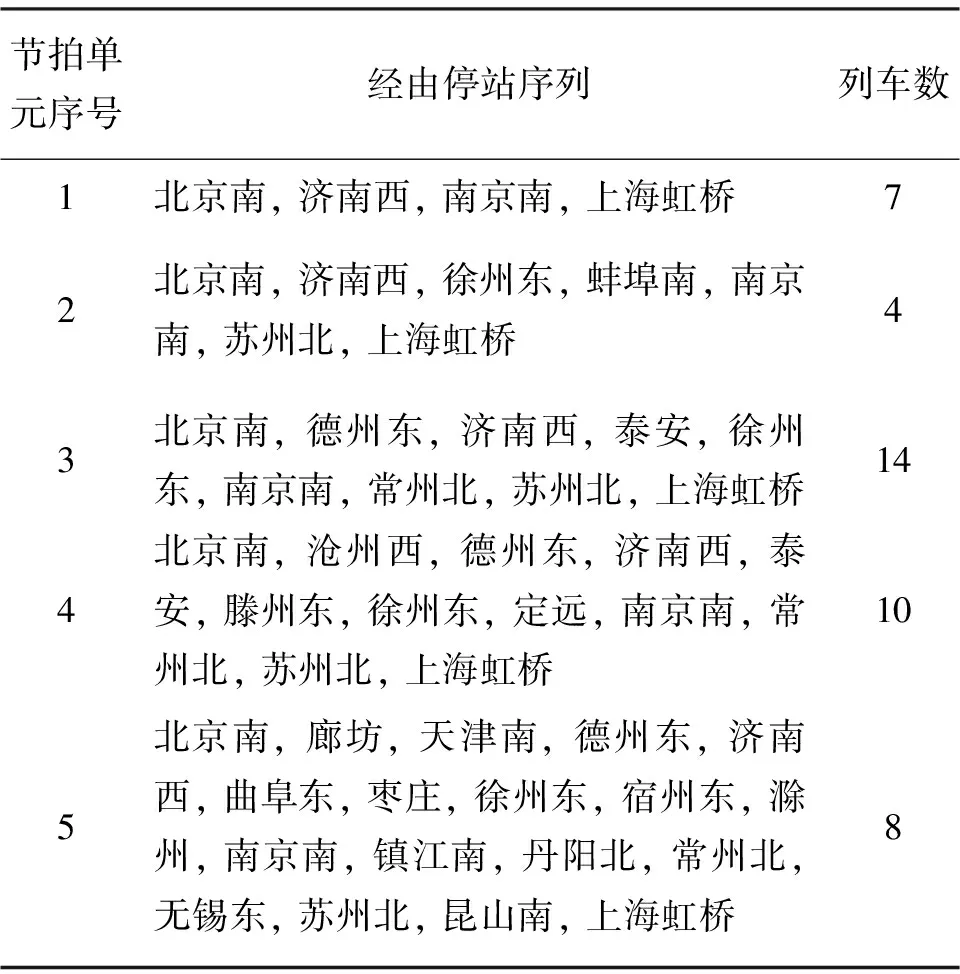
3 算例分析

结 语