一种改进的可适应变宽核密度估计器
金会赏,何玉林,常秀颖,王晓兰,蒋 捷
1)沧州职业技术学院信息工程系,河北沧州 061001;2)深圳大学计算机与软件学院大数据所,广东深圳 518060;3)深圳大学大数据系统计算技术国家工程实验室,广东深圳 518060
概率密度估计[1-2]是统计模式识别领域的一个重要研究方向,如何基于已有的数据集获得其未知的概率分布对于众多有监督机器学习算法的训练有至关重要的作用,例如贝叶斯分类器[3]、概率神经网络[4]和改型决策树[5]等.帕尔森窗口法[6]是一种经典的概率密度估计方法,又称核密度估计法.它是利用多个正态分布的叠加平均去拟合未知的概率分布,其中正态分布的均值为已知的数据点,方差为窗口宽度.窗口宽度对于概率密度估计的效果起着至关重要的作用:较小的窗口宽度将导致“过粗糙”的估计,较大的窗口宽度将引起“较平滑”的估计[7].
如何确定最优窗口宽度成为概率密度估计研究的关键点.当前的研究主要集中在以整个数据集为估计对象,即最优窗口宽度是针对整个数据集的.最优窗口宽度要使得真实概率密度函数和估计概率密度函数之间的均方差(mean square error, MSE)或者均积分方差(mean integrated square error, MISE)达到最小[7].常见的基于整个数据集进行概率密度估计的核密度估计器,包括靴样核密度估计器[8]、无偏交叉验证核密度估计器[9]和有偏交叉验证核密度估计器等[10-11].
除上述介绍的以整个数据集为估计对象的概率密度估计方法之外,还有一类以单个数据点为研究对象的概率密度估计方法,最优窗口宽度就是针对单个数据点的.KATKOVNIK等[12]提出的可适应变宽核密度估计器(kernel density estimator with adaptive varying bandwidth, KDE-AVB)正是这样一种专门针对单个数据点的概率密度估计方法.KDE-AVB为单个数据点寻找最为适合的核密度估计器窗口宽度,使得该点能够获得最为精确的概率密度估计值.为了寻找最优的窗口宽度,KDE-AVB使用了置信区间交叉(intersection of confidence intervals, ICI)法则[13],将置信区间上下界对应的最小值和最大值发生交叉的窗口宽度作为最优窗口宽度.
本研究为加快KDE-AVB对最优窗口宽度的寻找,提出一种改进的可适应变宽核密度估计器(improved kernel density estimator with adaptive varying bandwidth, IKDE-AVB),主要体现在引入了一种可变的标准差项因子去确定置信区间的上下边界.可变标准差项因子的引入不仅加快了KDE-AVB 搜索最优窗口宽度的速度,而且在一定程度上降低了“过平滑”概率密度估计现象发生的风险.仿真实验的结果证实了IKDE-AVB的可行性和有效性.相比于经典的KDE-AVB,IKDE-AVB不仅获得了更快的训练速度,同时提升了概率密度的估计精度.
1 核密度估计法
简便起见,仅以一维数据集为例展开研究.假设由随机变量X的N个观察值构成的数据集为D={x1,x2, …,xN},xn∈R,n=1, 2, …,N. 随机变量X真实的概率密度函数记作p(x), 其值未知.核密度估计法采用式(1)得到随机变量X的估计概率密度函数,即
(1)
其中,K(u)为高斯核函数,
(2)
h>0为窗口宽度,取值满足
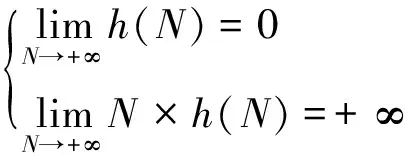
(3)
由式(1)可知,核密度估计法采用N个基正态分布
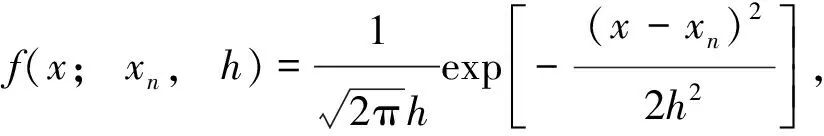
n=1,2,…,N
(4)
的叠加平均去拟合未知的概率密度函数p(x)[14]. 以下将通过具体实例来证实该结论.
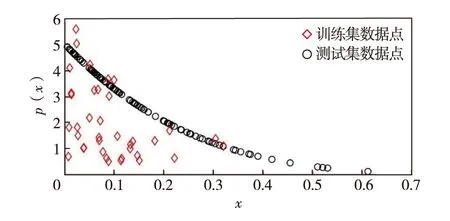
首先,随机生成如表1的20个服从标准正态分布的数据点;然后,采用式(1)估计概率密度函数,如图1.由图1可见,数据点密集区域对应的估计概率密度函数呈上凸趋势,而数据点稀疏区域对应的估计概率密度函数呈下凹趋势.这表明估计概率密度函数是由20个如式(4)的基于正态分布的叠加平均拟合而成的.值得注意的是,估计的概率密度函数与真实概率密度函数之间存在较大差异,这与窗口宽度的选取有关.为了清晰展示叠加平均拟合的思想,在此并未使用最优窗口宽度.
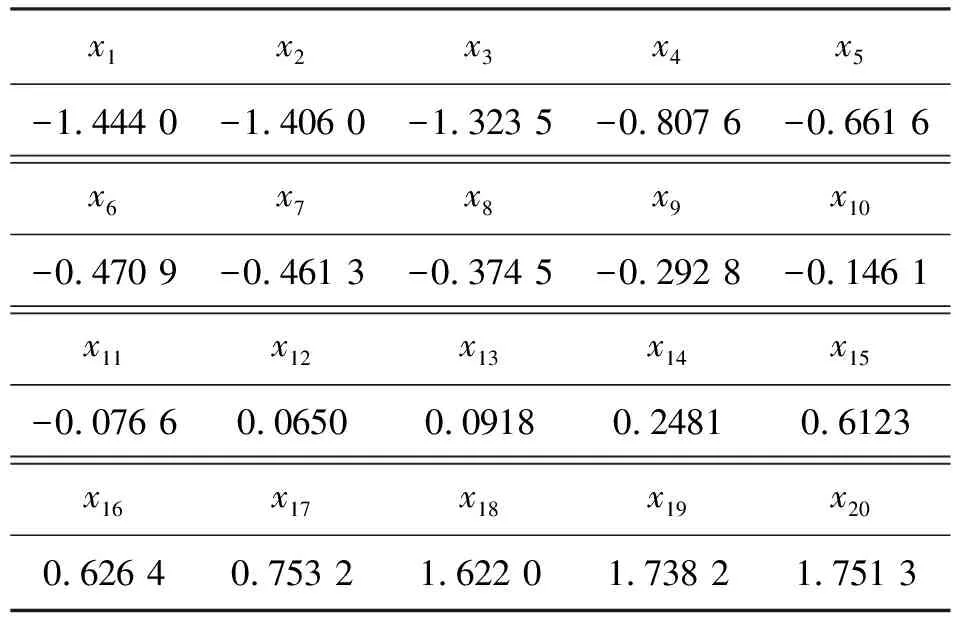
表1 核密度估计法(h=0.2)
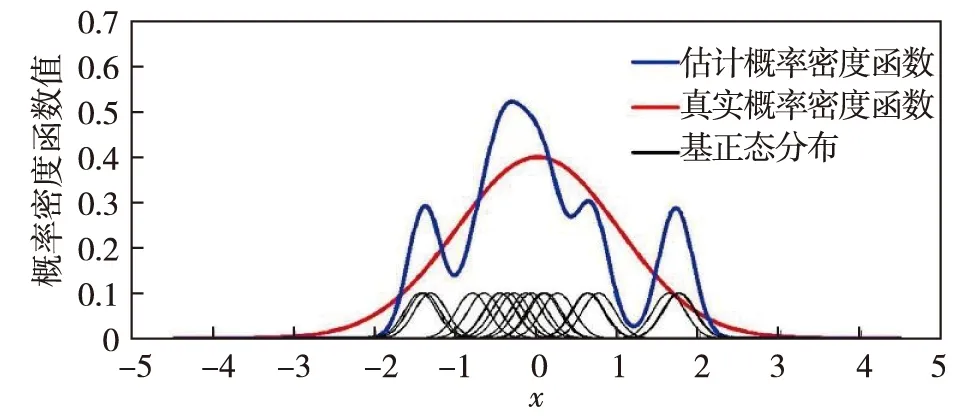
图1 核密度估计法效果图(h=0.2)Fig.1 Kernel density estimation method (h=0.2)
2 KDE-AVB
KDE-AVB[12]是一种专门针对单个数据点的概率密度估计方法.不同于针对整个数据集的窗口宽度选取方法,KDE-AVB为单个数据点寻找最为适合的核密度估计器窗口宽度,使得该点能够获得最精确的概率密度估计值.
对于数据集D中的任意数据点xn, 其中,n∈{1, 2, …,N}, KDE-AVB采用如下流程来确定仅针对xn的最优窗口h(n):
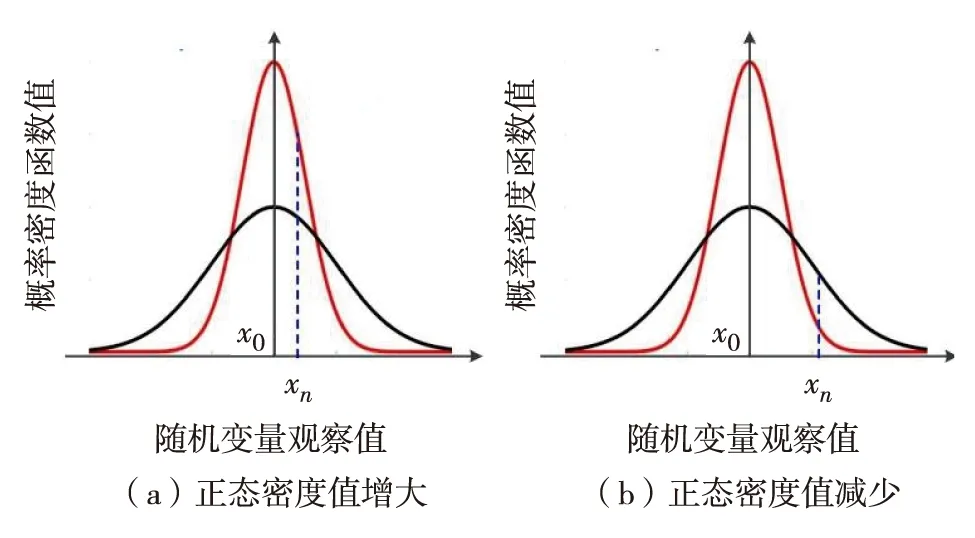
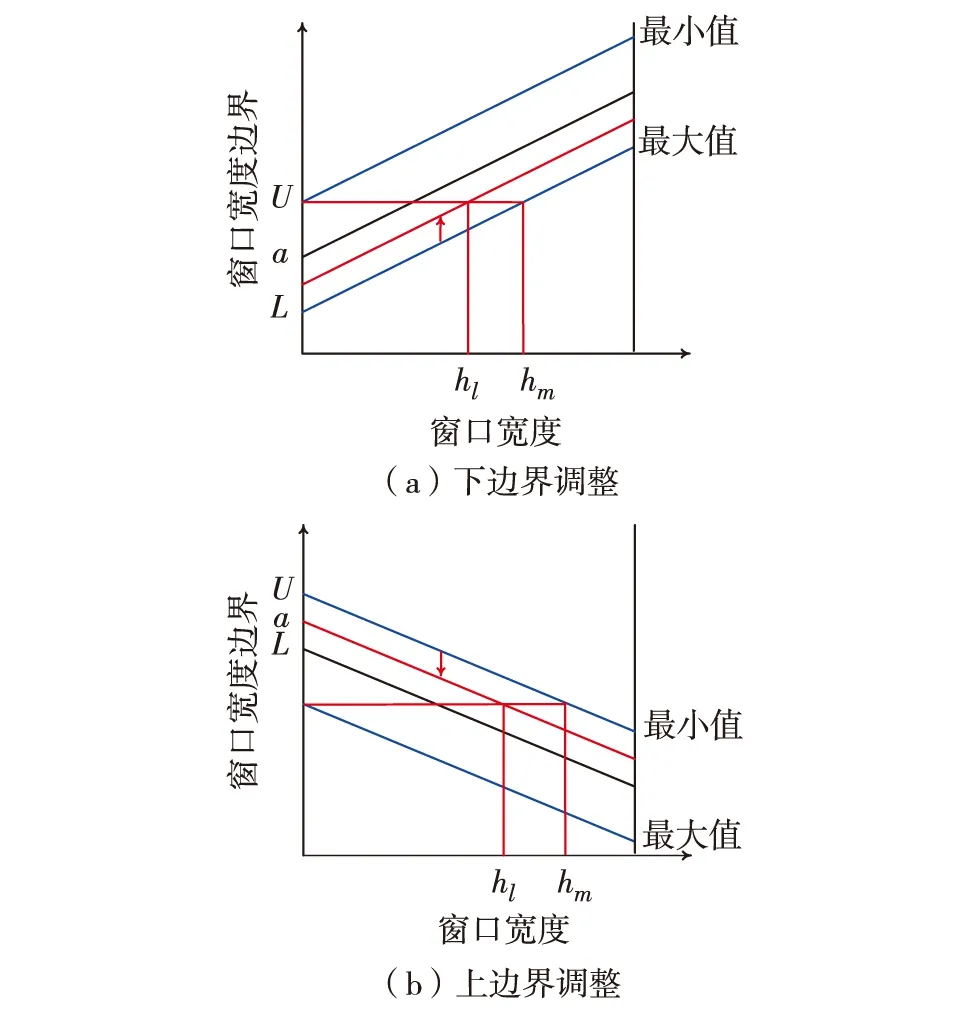
首先,生成一个窗口宽度集合H={h1,h2,…,hM},hm>0,m=1, 2, …,M,且h1 接着,计算每个窗口宽度对应的密度估计置信区间Im=[Lm,Um]. 其中,Im的下边界为 (5) 置信区间Im的上边界为 (6) 密度估计的标准差为 (7) 通过分析KDE-AVB的执行流程可知,对于含有N个数据点的数据集D, 和M个窗口宽度值的窗口宽度集合H, 针对D中的所有数据点进行概率密度估计的时间复杂度为O(NM). 当数据集的规模较大时,KDE-AVB需大量的计算时间来为数据集中的数据点寻找最优窗口宽度.本研究给出一种改进的可适应变宽核密度估计器IKDE-AVB,来加速对数据点最优窗口宽度的选取. (8) 图2 基正态分布随窗口宽度增加的变化Fig.2 Variation of base normal distribution with increase of bandwidth 随着h逐渐增大,则a呈单调上升或单调下降趋势.图2展示了f(x0;xn,h),n∈{1,2,…,N}随着h增大变化时的两种情况(红色曲线对应的窗口宽度大于黑色曲线对应的窗口宽度). 1)当a呈单调上升趋势时,假设L和U存在如图3(a)的变化趋势,可以发现,若让下边界L对应的蓝线沿着箭头指示的方向移动到红线位置,则对应的数据点x0的最优窗口将从hm变为hl, 其中, 任意的l,m∈{1, 2, …,M}. 由于hl 2)当a呈单调下降趋势时,假设L和U存在如图3(b)的变化趋势,可以发现,若让上边界U对应的蓝线沿着箭头指示的方向移动到红线位置,则对应数据点x0的最优窗口将从hm变为hl, 其中, 任意的l,m∈{1, 2, …,M}. 由于hl 图3 置信区间下边界和上边界调整Fig.3 Adjustment of lower boundary and upper boundary of confidence interval 通过上述分析可知,调整概率密度估计的置信区间的上下边界,能减少KDE-AVB搜索最优窗口宽度的次数.IKDE-AVB通过缩小标准差项因子Г来提升KDE-AVB搜索最优窗口宽度的速度.IKDE-AVB采用式(9)调整置信区间上下边界. (9) 图4 区间效用的图形化表示Fig.4 Illustration of interval utility 定义1区间效用区间[L,U]的效用被定义为S=|L|×|U|. 由定义1可得执行区间[a-Г×b,a+Г×b]和[a-ΘГ×b,a+ΘГ×b)的效用分别为 (10) (11) (12) 其中, ΔS为区间[ΘГ×b, Г×b)的效用, ΔS=(ΘГ×b)×(Г×b)=Θ(Г×b)2. 将式(10)和式(11)代入式(12),化简后可得 Θ2+Θ=1 (13) 由于Θ∈(0, 1), 取正数根Θ≈0.618, 即为GSR.事实上,很多学者已对GSR在实际应用中的优越性给予论证,如HE等[15]研究了基于GSR的目标追踪算法,KLEIDER等[16]利用GSR抽样处理麦克风阵列的数据挖掘问题,ZONG等[17]利用GSR设计了用于处理不平衡分类问题的加权极限学习机等,在此不一一赘述. 本研究在5种不同的概率分布数据集上,对KDE-AVB和IKDE-AVB的性能进行比较测试.这5种数据集包括正态分布(normal)、指数分布(exponential)、瑞利分布(Rayleigh)、贝塔分布(beta)和伽玛分布(gamma)数据集,对应的概率密度函数分别为 x∈(-∞, +∞) (14) (15) x∈[0, +∞) (16) (17) (18) 每种分布选用100个数据点(x1,x2, …,x100)作为训练集,选用20个数据点(y1,y2, …,y20)作为测试集.为保证实验的可重复性,详情请扫描论文末页右下角二维码,查看补充材料中的表S1—表S10所列具体的训练集和测试集.服从5种不同分布的数据集的可视化展示见图5—图9. 图5 正态分布数据集 (见补充材料表S1和S2)Fig.5 Data sets obeying normal distribution (see Tables S1 and S2 of the supplementary material) 图6 指数分布数据集 (见补充材料表S3和S4)Fig.6 Data sets obeying exponential distribution (see Tables S3 and S4 of the supplementary material) 图7 瑞利分布数据集 (见补充材料表S5和S6)Fig.7 Data sets obeying Rayleigh distribution (see Tables S5 and S6 of the supplementary material) 图8 贝塔分布数据集 (见补充材料表S7和S8)Fig.8 Data sets obeying beta distribution (see Tables S7 and S8 of the supplementary material) 图9 伽玛分布数据集 (见补充材料表S9和S10)Fig.9 Data sets obeying gamma distribution (see Tables S9 and S10 of the supplementary material) 令式(13)中的Г=5(沿用文献[12]中的参数设置).本研究采用“拇指原则”[18]确定启发窗口宽度的大小,即 (19) 其中,N为训练集中包含数据点的个数;σ为训练集的标准差.令H={0.001, 0.002, …, 5.000}, 共5 000个备选的窗口宽度值. 表2至表6分别给出了两种核密度估计器KDE-AVB和IKDE-AVB在5种不同概率分布数据集上的比较结果. 表2 当Г=5时KDE-AVB与IKDE-AVB在正态分布数据集上的对比结果 表3 当Г=5时KDE-AVB与IKDE-AVB在指数分布数据集上的对比结果 由表2至表6可见,IKDE-AVB的最优窗口宽度搜索次数以及估计误差(真实密度值和估计密度值之差的绝对值)都小于KDE-AVB: 1)在正态分布数据集上,IKDE-AVB的最优窗口宽度平均搜索次数为7,比KDE-AVB降低约25%,同时IKDE-AVB的估计误差为0.056,比KDE-AVB降低了约63%; 2)在指数分布数据集上,IKDE-AVB的最优窗口宽度平均搜索次数为16,比KDE-AVB降低约50%,同时IKDE-AVB的估计误差为0.056,比KDE-AVB降低了约59%; 表4 当Г=5时KDE-AVB与IKDE-AVB在瑞利分布数据集上的对比结果 3)在瑞利分布数据集上,IKDE-AVB的最优窗口宽度平均搜索次数为21,比KDE-AVB降低约50%,同时IKDE-AVB的估计误差为0.056,比KDE-AVB降低了约55%; 4)在贝塔分布数据集上,IKDE-AVB的最优窗口宽度平均搜索次数为123,比KDE-AVB降低约64%,同时IKDE-AVB的估计误差为0.056,比KDE-AVB降低了约40%; 表5 当Г=5时KDE-AVB与IKDE-AVB在贝塔分布数据集上的对比结果 5)在伽玛分布数据集上,IKDE-AVB的最优窗口宽度平均搜索次数为18,比KDE-AVB降低约33%,同时IKDE-AVB的估计误差为0.056,比KDE-AVB降低了约55%. 以上实验结果证实了IKDE-AVB的可行性和有效性.相比经典的KDE-AVB,IKDE-AVB具有更快的训练速度和更低的估计误差.此外,由于IKDE-AVB减少了最优窗口宽度的搜索次数,因此更倾向于选择较小的窗口宽度,这在一定程度上降低了“过平滑”概率密度估计现象发生的风险. 表6 当Г=5时KDE-AVB与IKDE-AVB在伽玛分布数据集上的对比结果 本研究通过引入了一种可变的标准差项因子确定置信区间的上下边界,提出了一种改进的可适应变宽核密度估计器.相比经典的可适应变宽核密度估计器,改进的可适应变宽核密度估计器不仅具有更快的训练速度,同时提高了概率密度估计的精度.未来,我们将试图将改进的可适应变宽核密度估计器IKDE-AVB推广到具体的实际应用中[19-20],尤其是以随机样本划分(random sample partition, RSP)数据模型[21-23]为基础的大数据管理与分析中.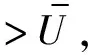
3 IKDE-AVB
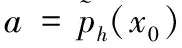

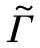
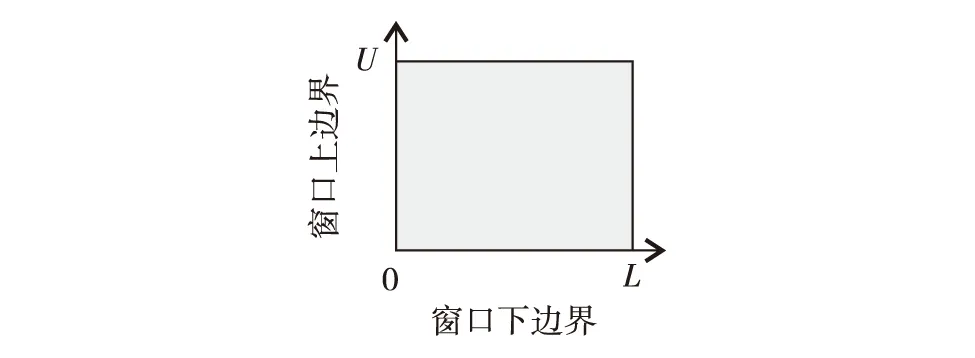
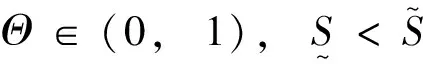
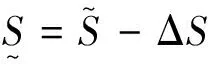
4 实验结果与分析


结 语

