激光捷联惯导振动耦合问题的精细建模

姚志强，雷宏杰，宋汉文，张 懿

(1.航空工业西安飞行自动控制研究所，西安 710100；2.同济大学 航空航天与力学学院，上海 200092)

近年来，随着工业上对精密仪器精度要求的不断提高，角振动问题日益受到广泛学者的关注[1-2]。典型的精密仪器——激光捷联惯导中，激光陀螺的性能对惯性导航的精度具有重要影响。为了消除小角速度输入下陀螺无输出的闭锁效应，激光陀螺工作时，其抖动轮在持续的抖动中[3]，因此陀螺抖动是IMU除了来自载体的振动和冲击之外，主要的振动源。工作条件下，陀螺的抖动会引起惯性测量单元(IMU)的角振动，若该角振动在其它陀螺的敏感轴方向分量为零，则陀螺抖动引起的振动相互解耦，那么理论上陀螺在IMU中的性能指标可以达到单个陀螺测试的性能指标；反之，若该角振动在其它陀螺的敏感轴方向分量不为零，则表明振动存在耦合，陀螺性能将下降。本文通过对IMU的振动建模，提出了弹性椭球的概念，给出了IMU振动解耦的设计约束。

IMU的减振研究主要为减振模式的分析[4]、减振系统的设计[5-7]及减震器特性分析[8-10]。尽管研究人员发现IMU的质心与弹性中心的重合可以实现线振动与角振动的解耦，惯性主轴与弹性主轴重合可以实现角振动相互间的解耦[11-13]，然而，尚缺乏这一结论的理论导出过程。

本文针对陀螺抖振引起的IMU振动，借助欧拉方程和拉格朗日方程导出了六自由度振动方程。为了更为直观的描述使振动方程解耦数学约束，本文定义了弹性椭球这一概念，并分析了弹性椭球与惯性椭球不同位置关系下IMU的振动响应特点。

1 IMU振动建模

振动方程的建立采取惯性坐标系P-xyz作为参考，各坐标轴方向平行于静态时IMU的惯性主轴方向。通常，惯性测量单元橡胶隔振系统安装有8个上下对称布置的隔振器[14]，如图1所示。由于IMU台体的刚度远大于减振器刚度，建模中将其视为六自由度刚体。

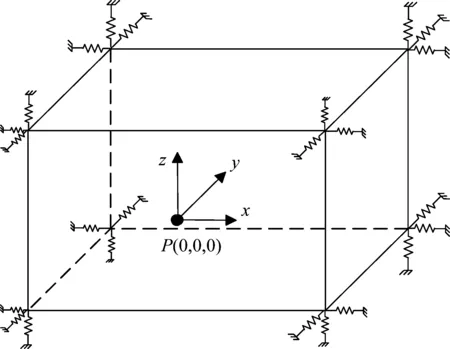
图1 IMU及其支撑系统示意图Fig.1 Sketch map of the IMU and its support system

2 基于动量矩定理的欧拉方程

设IMU绕点P转动，固连于刚体的P-x*y*z*作为连体坐标系。系统静止时，P-x*y*z*与P-xyz重合。动量矩定理在该坐标系下的投影式为[15]

(1)

式(1)可改写为

(2)

上式即为刚体定点转动欧拉运动方程。

2.1 基于拉格朗日方程的振动方程

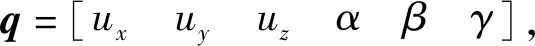
第i个支撑点(xi,yi,zi)处的位移变化量，即弹簧的变形量，由平动和转动两部分组成

(3)

CγCβCα为三次转动的方向余弦矩阵。设系统的角振动可视为无限小转动，则方向余弦矩阵可简化为

(4)

将式(4)代入式(3)可得

(5)

由于实际的IMU设计通常采用三向等刚度减振器，若振动中不考虑重力势能的变化，仅考虑弹性势能，则系统的势能可表示为

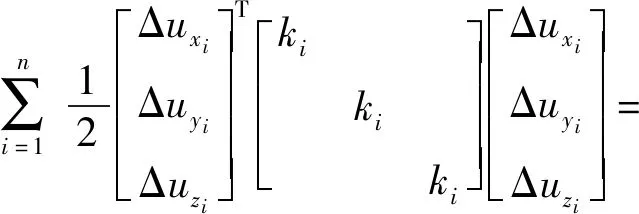
(ziβ)2+(xiγ)2+(yiα)2))+2(uxziβ+uyxiγ+uzyiα)-2(uxyiγ+uyziα+uzxiβ)-2(yiγziβ+ziαxiγ+xiβyiα))

(6)

若静止状态下，系统质心的位置坐标为(xm,ym,zm)，则根据式可得dt时间微段内，质心的位移增量为

(7)

进而质心速度为

(8)

系统的动能可表示为

(9)

根据式(9)和式(6)可以建立拉格朗日函数L=T-V，存在拉格朗日方程

j=1,2,3,4,5,6

(10)

将式(9)及式(6)代入式(10)，对于线振动，即j=1,2,3，可得：

(11)

对于角振动，需要考虑惯性坐标系与主轴坐标系之间的相互转化。可将式(10)改写为

j=4,5,6

(12)

(13)

(14)

将式(2)代入式(14)，将出现角度、角速度和角加速度的乘积项，通常该乘积项不可忽略。然而，在捷联惯导系统中，激光陀螺机械抖动机构的抖动频率一般在100～400 Hz[16]，国内相关研究院所生产使用的高频激光陀螺的抖动频率也小于1 000 Hz。因此，惯导系统的角振动频率不会超过1 000 Hz。由于角速度和角加速度与角度满足导数关系，对于无限小转动，因此可以认为角速度和角加速度都为无限小量，无限小量的乘积项可视为高阶无穷小略去。因此，上式可线性化为

(15)

此外，我们有：

(16)

结合式(12)、式(15)及式(16)可得

(17)

(18)

由式(17)、式(18)及式(11)可得系统的振动方程

(19)

其中质量矩阵为

M=

(20)

刚度矩阵为

K=

(21)

广义力为

(22)

需要特别指出的是，上述结果的导出是建立在以下两点简化之上的：① IMU作无限小转动，方向余弦矩阵式(4)忽略了二阶小量；② 式(17)的导出忽略了IMU三个角振动的二次交叉耦合项。

2.2 振动方程的简化

本文只考虑陀螺抖动引起IMU的振动，从式(20)和式(21)可以看出，当

xm=0,ym=0,zm=0

(23)

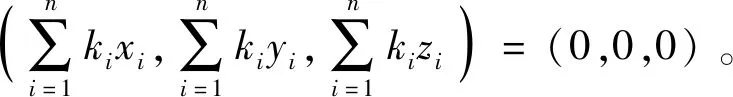
(24)

此时，角振动方程可以独立写作

(25)

3 弹性椭球

注意到刚度矩阵式(25)中刚度矩阵各个元素的表达式，与质点系惯性张量的矩阵表达式极为相似，该矩阵定义为

(26)

本文定义S为弹性张量的矩阵表达式。其对角元称为弹性矩，非对角元称为弹性积。质点系惯性张量与弹性张量矩阵表达式唯一不同的是质量被弹簧刚度所替换。因此，与惯性张量类似，在空间中应该存在一个弹性椭球满足方程

Sxxx2+Syyy2+Szzy2-2Sxyxy-

2Sxzxz-2Syzyz=k2

(27)

从解析几何知道，一个椭球在空间中必然存在三根正交的主轴。如果我们把这三个主轴取作坐标轴，弹性中心作为坐标原点，那么弹性椭球的方程将简化为

Sxx2+Syy2+Szy2=k2

(28)

弹性椭球的主轴称为弹簧对于弹性中心的弹性主轴，相应的弹性矩Sx,Sy,Sz称为主弹性。那么，当坐标轴方向进一步与弹性主轴平行时，角振动方程退化为

(29)

综上所述，要使得IMU六个自由度上的振动完全解耦，需要满足以下两个条件：① IMU的质心与弹性中心重合(线振动与角振动解耦);② IMU的惯性主轴与弹性主轴重合(角振动间相互解耦)。

工程实际中，可以通过合理布局减振器相对系统质心的坐标位置，实现质心与弹性中心重合且惯性主轴与弹性主轴重合。

4 仿真验证

上述理论推导中，均未考虑弹簧阻尼的影响，假设阻尼矩阵与刚度矩阵形式相同。某型号减震器的通过设计参数计算出的弹簧刚度和阻尼分别为

k=84 739(N/m),c=53.68(N·s/m)

(30)

由于IMU被视为刚体，IMU内部的结构阻尼予以忽略，系统的阻尼完全由减震器提供，因此只需将式(21)中的弹性系数改为阻尼系数即可得到系统的阻尼矩阵。本文只考虑抖振的影响，三只陀螺的抖振频率依次为550 Hz、606 Hz、714 Hz，以引起IMU产生单位静扭转的力矩为幅值，抖动频率为激励频率模拟激励信号。

某型号IMU的几何尺寸为90 mm×138 mm×129 mm，以质心为坐标原点，静止状态下惯性主轴为坐标轴，支撑系统如图1所示。仿真算例中，计算了图2所示的四种设计状态下IMU的振动响应。图2(a)为质心与弹性中心重合，惯性主轴与刚度主轴平行;图2(b)为质心与弹性中心重合，惯性主轴与刚度主轴不平行；图2(c)为质心与弹性中心不重合，惯性主轴与刚度主轴平行；图2(d)为质心与弹性中心不重合，惯性主轴与刚度主轴不平行。图中长方体表示IMU，浅灰色椭球表示惯性椭球，深灰色椭球表示弹性椭球。

不同设计状态下的绕Z轴角振动及线振动对比如图3～图5所示。

(a)双心重合双轴不重合Z轴角振动

(b)理想设计Z轴角振动图3 双心重合双轴不重合与理想设计IMU对比Fig.3 The comparison between the idealized IMU with the IMU in which the two centers coincide and the two axis mismatch

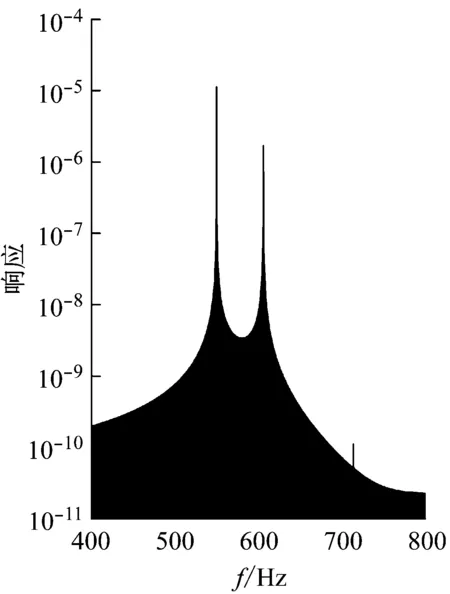
(a)沿Z轴线振动

(b)绕Z轴角振动图4 双心不重合双轴平行IMU响应Fig.4 The response of the IMU in which the two centers mismatch and the two axis parallel

(a)沿z轴线振动

(b)绕z轴角振动图5 双心不重合双轴不平行IMU响应Fig.5 The response of the IMU in which the two centers mismatch and the two axis do not parallel

为了进一步整体对比不同设计情形下IMU的响应特点，本文将以上四种情形在陀螺工作频率下的振动响应峰值绘制成柱状图，如图6所示。

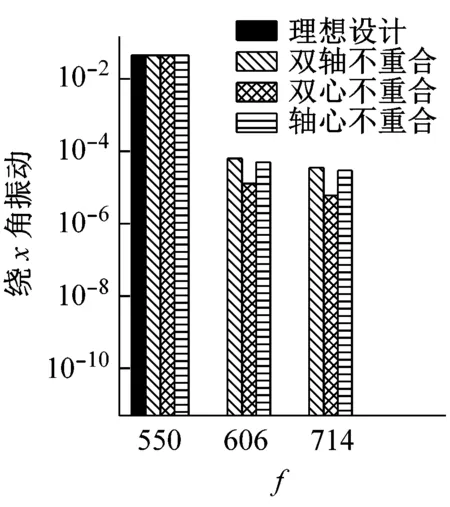
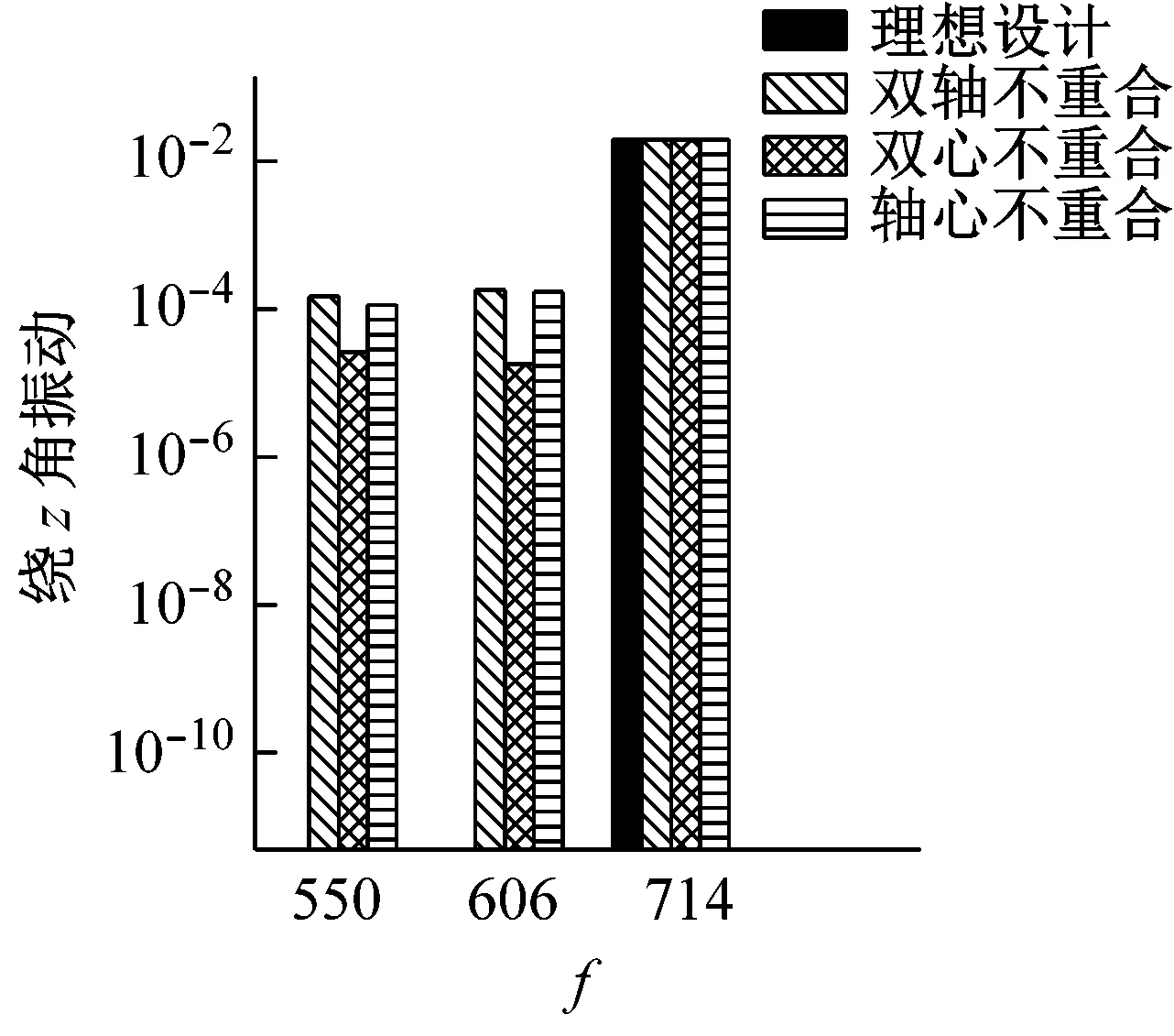
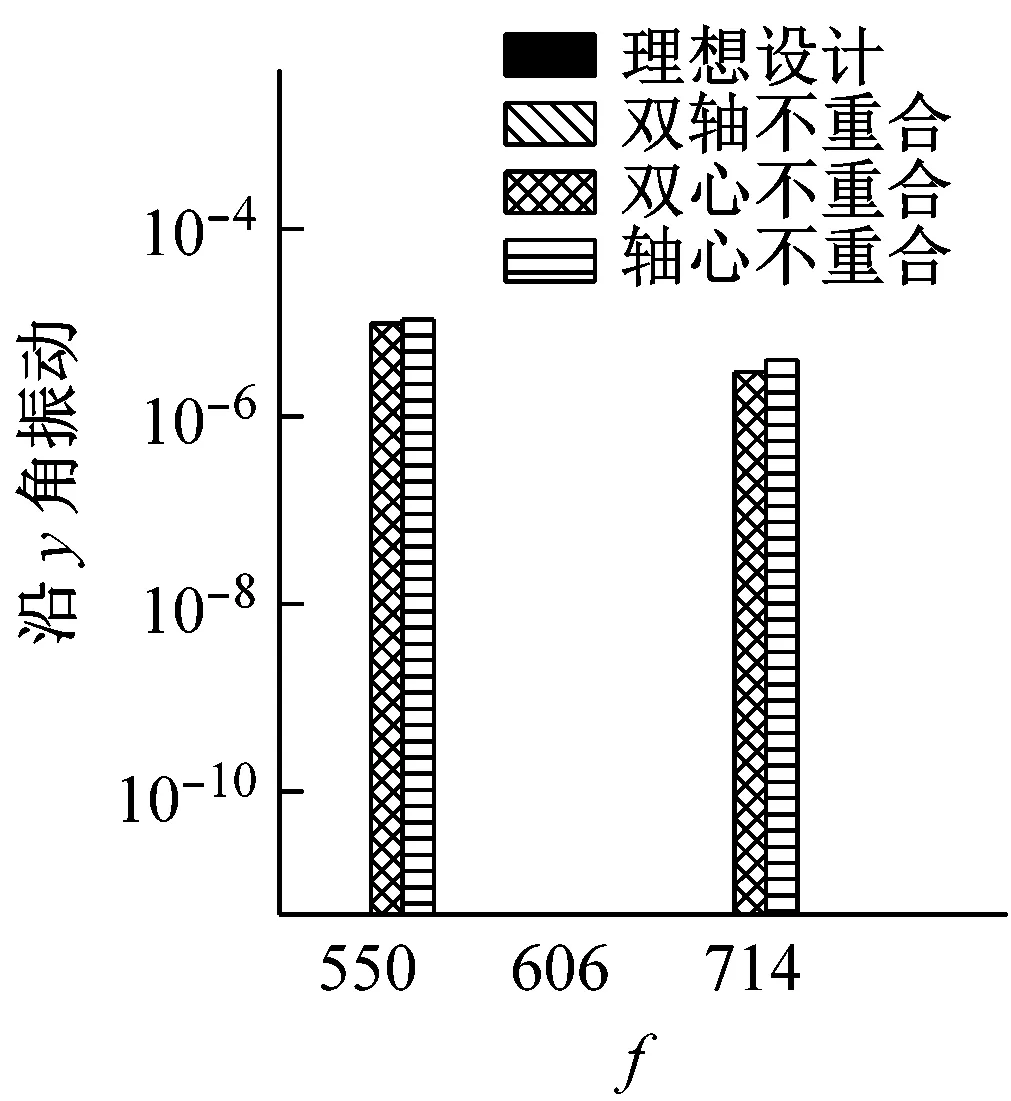
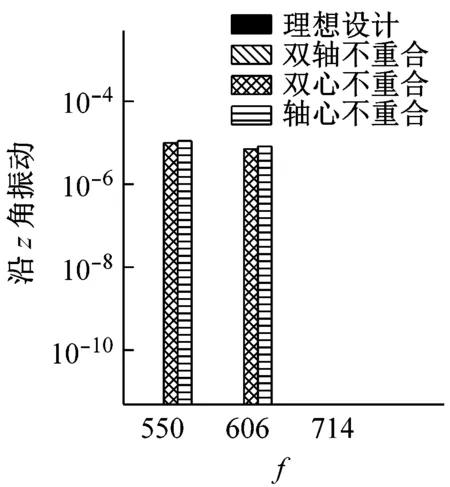
图6 不同设计状态下IMU响应峰值对比Fig.6 The peak values of the response of the IMU under different designs

分析图6可得到以下结论：

(1)双心重合且双轴重合时，三只陀螺的抖动引起的IMU角振动相互独立，且不会引起IMU线振动。

(2)双心重合可以避免陀螺抖动引起的耦合线振动。

(3)系统偏心和双轴不重合都会引起IMU不同程度的耦合角振动和耦合线振动。

5 结 论

激光捷联惯导工作状态下，为了消除闭锁效应，激光陀螺需要保持持续的抖动，该抖动是IMU的主要振动源。工程实践中，三只激光陀螺在IMU中逐个单独工作的精度远高于同时工作的精度，进一步的分析表明同时工作时陀螺间的耦合振动是造成精度下降的主要原因。本文旨在提出陀螺振动解耦的理论约束。

为了实现IMU的振动解耦，本文从动量矩定理和拉格朗日方程出发建立了任意设计状态下IMU的振动方程。对振动方程的深入分析表明：若质心与弹性中心重合，振动方程将简化为线振动与角振动解耦的形式；在此基础上，若惯性主轴与弹性主轴重合，振动方程将在六个自由度上完全解耦。为了直观描述这一结论，本文定义了弹性张量和弹性椭球。通过仿真计算了IMU不同设计状态下，具体表现为弹性椭球和惯性椭球不同位置关系下，IMU的振动响应，验证了本文导出的振动解耦理论约束。