某千米级摩天大楼的风振控制研究
陈 勇,金 钊,陈 鹏
(中国建筑东北设计研究院有限公司 技术中心,沈阳 110006)
21世纪以来,超高层建筑蓬勃发展,随着高层建筑在高度上的迅速发展,抗风问题变得尤为重要,使得风荷载成为高层建筑设计中一个需要着重考虑的问题[1]。设计中不仅需要结构具有足够的抗风能力,还对舒适度提出较高的要求。对于不满足抗风要求的结构,进行结构振动控制可以有效地减小结构动力响应。
对于超高层建筑的风振控制,若采用加大结构抗侧刚度将十分不经济,效果不一定明显反而会由于侧向刚度的增大导致地震作用放大。研究表明[2]利用消能减振装置(例如黏滞阻尼器、调频质量阻尼器等)能有效控制风荷载下的结构侧移与结构振动加速度。Lu等[3]和任军等[4]分别采用质量阻尼器对上海中心大厦以及深圳地王大厦进行了风振控制的相关研究,结果均表明质量阻尼器对于风振响应有较好的控制作用。在这些研究中多围绕TMD的参数计算以及优化,并辅以其他主被动手段对控制效果展开研究。
而对于黏滞阻尼器,相关的研究主要围绕阻尼器的设计上,如阻尼器非线性指数与阻尼器的耗能能力、稳定性等的关系[5],活塞直径、黏滞阻尼黏度、冲击速度与阻尼力的关系[6]。对于黏滞阻尼器的运用,墨西哥Torre Mayor大厦[7],波士顿111 Huntington大楼[8],北京银泰中心[9],菲律宾Saint Francis香格里拉塔[10]等多高层建筑均采用黏滞阻尼器达到了理想的振动控制效果。
在这些相关的研究以及应用实例均说明了质量阻尼器和黏滞阻尼器的控制效果,可以将其运用于结构的振动控制中。本文的研究以中国建筑总公司提出的千米级高层建筑为对象,运用有限元软件ANSYS进行风振分析。其中,风荷载依据刚性模型风洞实验结果,经相似比关系转换得到实际结构表面的脉动风荷载时程。由于所得到的风振响应中,结构的侧向位移较大,部分扭转响应超过规范要求,本文采用了质量阻尼器和黏滞阻尼器对结构进行风振响应控制研究。
1 建筑概况及有限元模型
千米级摩天大楼拟建在中国辽宁大连市,整个建筑是四座千米级塔式超高层建筑的连合体,主体结构高度达1 000 m。每个塔体均为巨型钢框架-钢板核心筒结构,通过每隔100 m设置一个两层的平台将其连接为整体,整个建筑效果图见图1。

图1 结构示意图Fig.1 Effect drawing of the kilometer skyscraper
根据《抗震规范》的规定,建筑拟建地上的框筒结构适用最大高度为300 m,本工程结构高度为1 000 m,为超限高层。同时,考虑到大连市近海,海风较大且季节性强,100年一遇基本风压高达0.75 kN/m2,故需要对该超限高层进行抗风研究。
本文采用通用有限元分析软件ANSYS建立了该千米级摩天大楼的有限元分析模型(见图2)。该结构属于钢筋混凝土框筒结构体系,建模采用Beam44单元模拟梁柱构件,Shell63单元模拟楼板及剪力墙。

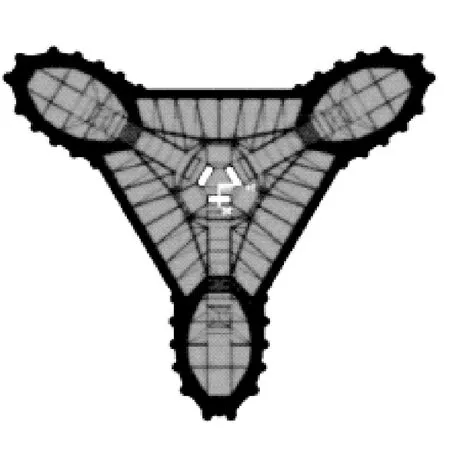
图2 千米级摩天大楼的有限元模型Fig.2 Finite element model of the kilometer skyscraper
对该有限元模型进行了自振分析,得到模型的振型及相对应的频率,结果如图3所示。从自振结果中可以看出结构前2阶振型为整体剪切平动,第3阶振型为整体扭转振动。


图3 结构振型及频率(ANSYS)Fig.3 Vibration shape and frequency of natural vibration
2 刚性模型测压试验
在对该千米高层进行风振分析之前,在哈尔滨工业大学风洞与浪槽联合实验室的小试验段中对其进行了刚性模型测压试验,以此获取风荷载时程数据。试验段的截面宽度为4.0 m,高度为3.0 m,为满足风洞阻塞率的要求(<5%),模型几何缩尺比选为1∶600。对于风剖面的模拟,本文采用格栅以及粗糙元来模拟,并同时考虑该大楼周围900 m半径范围内建筑群的影响。最终模型以及试验现场如图4所示。

图4 刚性模型测压试验现场Fig.4 Wind tunnel test of the kilometer skyscraper
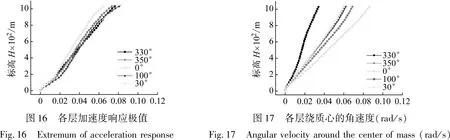
图5给出了平均风速剖面、湍流度剖面与荷载规范的对比,其中参考高度Zref取为1.67 m(对应实际高度为1 000 m),参考风速Vref取为1.67 m高度处的风速,该风速与0.58 m(对应实际高度为350 m,即B类地貌的梯度风高度)处的风速相同。图6为0.1 m高度处(相当于实际60 m处)顺风向脉动风功率谱密度,风场模拟结果与Karman谱较为接近。可以看出,本次试验风场的模拟结果良好。
定义0°风向角是从建筑正北方向吹来的风。试验时,模型固定在试验段底部转盘上,由0°开始逆时针旋转到360°,每隔10°测量一次,共进行36个风向的测量,通过比较360°与0°风向角结果来确定试验的稳定性,图7给出了各风向角示意图。设定试验风速为10 m/s,测压信号采样频率为625 Hz,采样时间20 s,每个工况采集5个样本。

图5 平均风速和湍流度剖面对比Fig.5 Spatial distributions of wind velocity and turbulence intensity
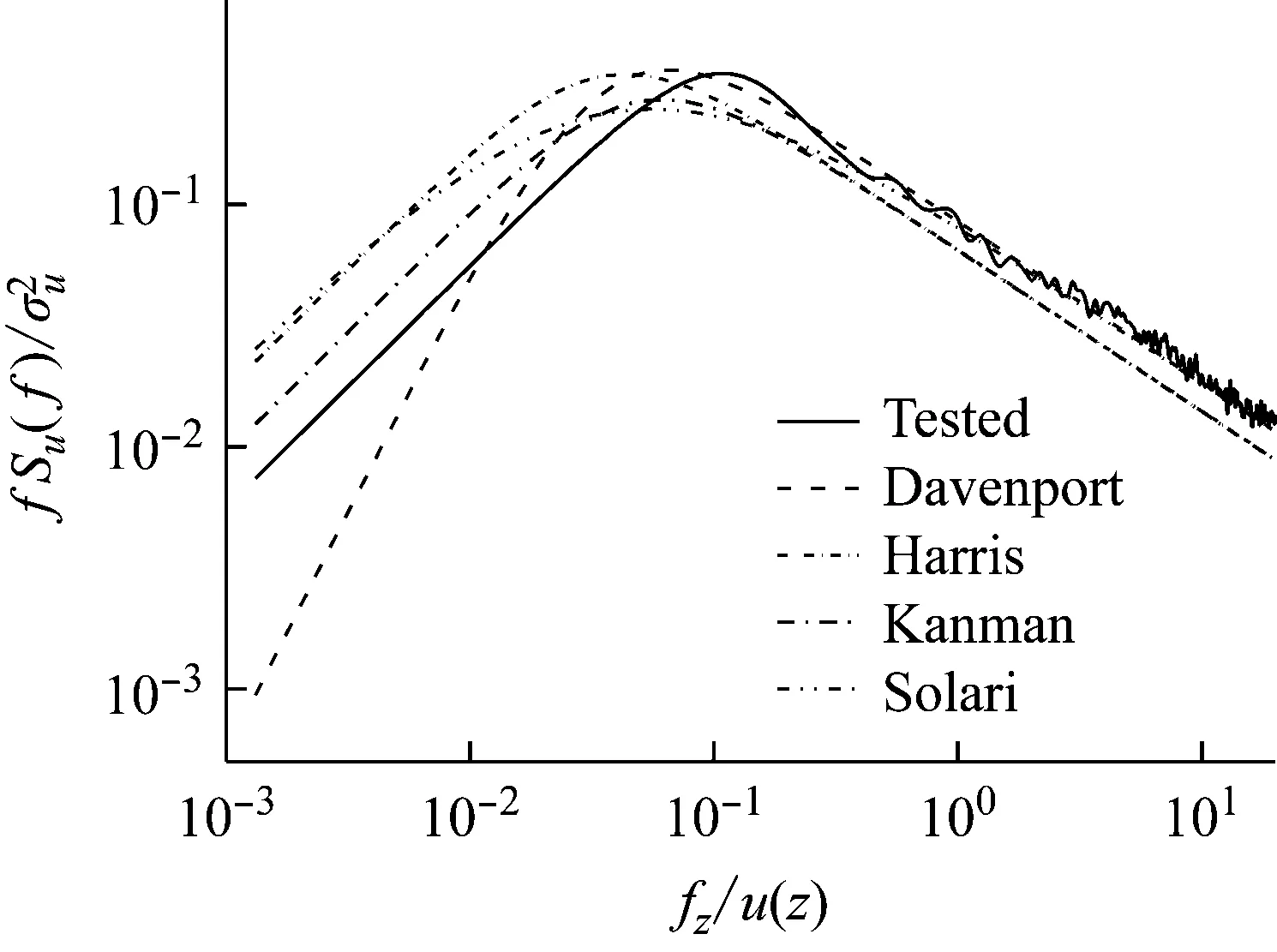
图6 顺风向脉动风功率谱密度对比Fig.6 Comparison between the wind velocity spectrum and the Von Karman spectrum

图7 各风向角示意图Fig.7 Sketch of wind direction
由于风洞试验测点数较多,超出单次测量测点的允许数目,因此实验中共进行了不同高度范围内共5个批次的测量工作。其中风洞试验模型表面测点分布及批次、典型高度的测点分布如图8所示。
测量时,由于各批次的不同步性,采用了局部神经网络的方法进行了修正,修正的具体方法已经发表于文献[11]。图9和图10给出了风荷载时程修正前后的风压系数时程曲线及其频谱,可见,修正前后风荷载的频谱特性未发生明显变化。

(a)整体测点布置
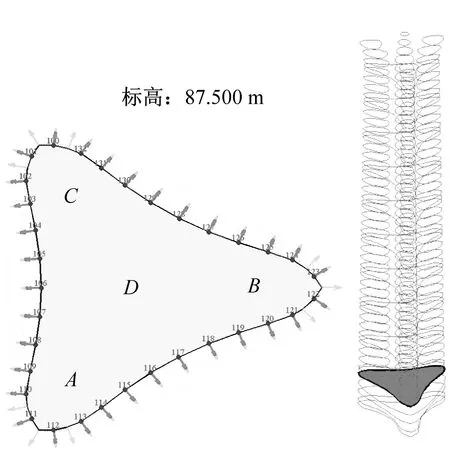
(c)标高87.5 m测点布置图8 风洞试验模型表面测点分布Fig.8 Pressure tap distribution of the kilometer skyscraper
当获得了结构表面脉动风荷载时程后,根据风洞模型与实际结构的相似比换算,即可得到作用于实际结构的脉动风荷载时程以及加载步长。
为了方便工程设计中对风荷载的合理确定,需要明确最不利的风向,从而详细考察最不利荷载作用下结构的受力情况,保证结构设计的合理性。为了初步确定最不利风向,对建筑的风力系数随风向角变化的规律进行研究,风力系数分为力系数、力矩系数和扭矩系数(各建筑楼体轴示意见图7),定义如下:
(1)力系数
(1)
(2)
(3)
式中:CFx,CFy为建筑整体的平均x、y向力系数;CF为建筑整体的平均合力系数;Fx,Fy为建筑整体的平均x、y向合力(N);Ax,Ay为建筑整体的平均x、y向投影面积(m2);Ai为测点i附属面积(m2);cosαi,sinαi为测点i所在位置处的x、y向方向向量
(2)力矩系数
(4)
(5)
(6)
式中:CMx,CMy为建筑整体的平均x、y向力矩系数;CM为建筑整体的平均合力矩系数;Mx,My为建筑整体的平均x、y向合力矩(N·m);zi为测点i到弯矩计算点的距离(m);L为计算段的长度(m)
(3)扭矩系数

(7)
式中:CMz为建筑整体的平均扭矩系数;Mz为建筑整体的平均扭矩(N·m);xi,yi为水平投影下,测点i距计算扭矩参考点的相对坐标(m);A为建筑整体的表面积(m2);R为建筑整体水平投影半径(m),取110 m。
本文给出了建筑结构在各个风向角下整体力系数与整体力矩系数与风向角的关系,如图11所示。综合考虑整体力系数与整体力矩系数确定最不利风向角为330°。
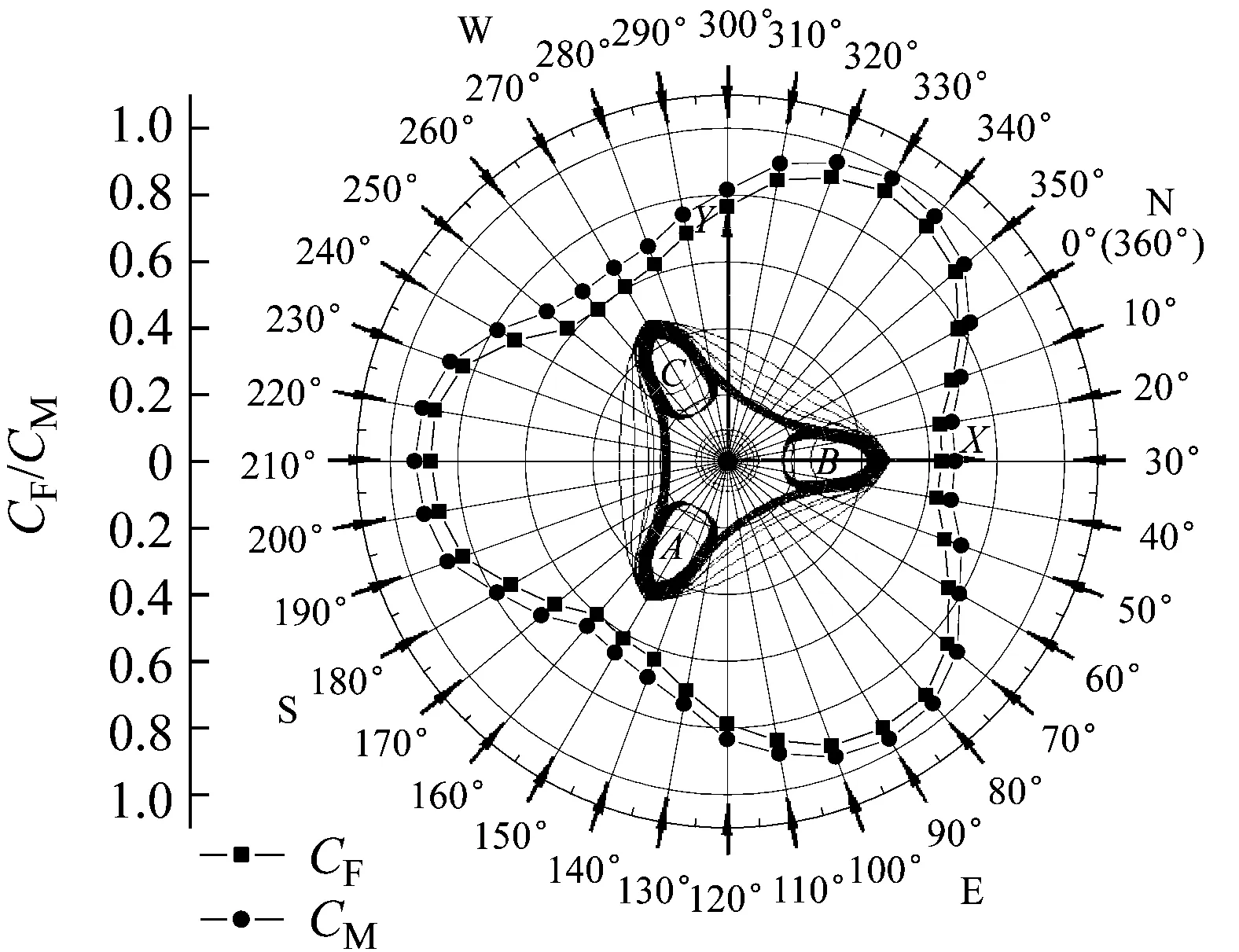
图11 各风向角合力、合力矩系数极坐标图Fig.11 Resultant coefficient
3 结构的风振响应分析
对结构进行风振响应分析时采用时程分析法,根据风洞试验结果确定结构有限元模型上各点的风压时程,在时域内数值求解结构动力微分方程,得到结构响应X(位移、速度、加速度等)的时程,然后对响应样本进行统计分析,求得风振响应的均值、均方差和相应的频谱特性,再由式(8)统计得到极值响应。
(8)

进行风振响应分析时,阻尼比取0.02,考虑到该结构的重要性,对于结构的位移响应分析,采用100年重现期的风荷载进行计算,给出各风向下的各层质心侧移极值、层间位移角极值及位移比极值和均值。对于风振舒适度响应分析,根据《建筑结构荷载规范》(GB 50009—2012)以及《高层建筑混凝土结构技术规程》(JGJ 3—2010)中的相关规定,采用10年重现期的风荷载进行计算,给出结构各层质心加速度响应以及各层绕质心角速度响应。其中风向角及建筑体轴的定义如图7所示。
为了下文描述该四塔连体结构风致响应的方便,对可能出现的响应名词进行说明。
假定结构各层各个塔楼在风致振动过程中不发生相对转动,然后将各层中间塔楼的位移转化为三分量位移。首先,定义X、Y方向的合位移为结构的质心侧移(图12b中U)。其次将结构的层间位移角定义为层间最大位移Δu与层高h之比。对于扭转效应,结合《高层民用建筑钢结构技术规程》(JGJ 99—2014)中对扭转效应的评价指标,采用位移比进行衡量,本文位移比定义为max(U1,U2,U3)/U(见图12)。
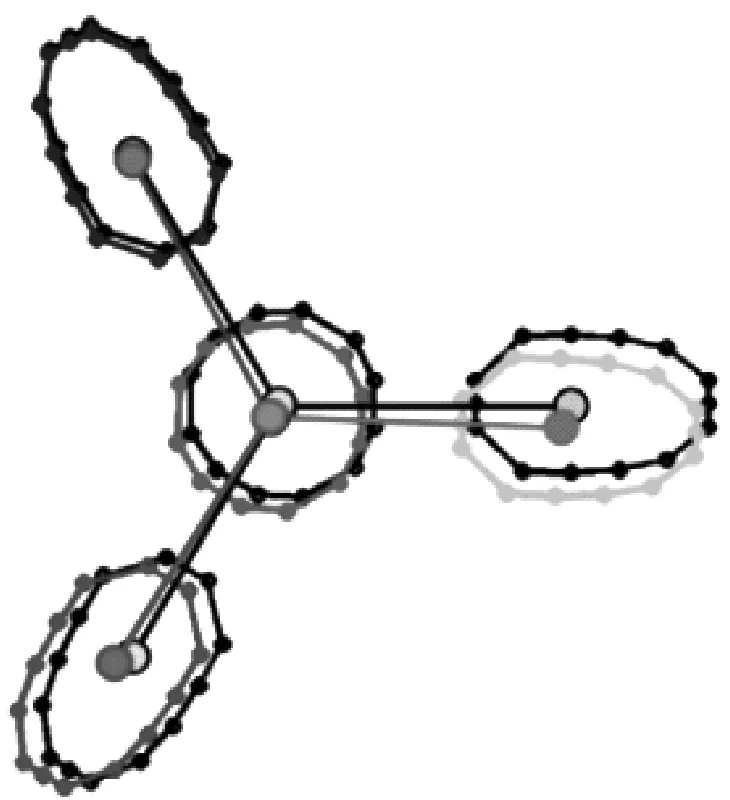
(a)某时刻真实位移
图13~图17给出了各风向角下结构的位移以及舒适度响应。从风振响应结果中可以看出,对于结构的位移响应,330°为最不利风向,在该风向角下,标高445 m附近的最大层间位移角达2.21×10-3>1/500,略超出《高层建筑混凝土结构技术规程》限值。除此之外,通过位移比的响应结果可以看出,该结构的扭转响应较大,0°为扭转的最不利风向,该风向角下的位移比极值达1.425,超过了《建筑抗震设计规范》的相关规定。因此在对结构进行舒适度响应分析时,考察了结构的扭转舒适度,除了给出各层加速度响应极值外,也给出了各层绕质心的角速度作为设计参考。
最后,本文针对不同的风振响应将最不利响应结果进行汇集,结果如表1所示。从表中可以看出,对于该结构,层间侧移角极值超过了规范要求。由于位移比反映了结构的扭转响应,且位移比极值较大,说明整个结构的抗扭刚度较小。对此,应该采取一定的风振控制措施对该结构进行风振响应控制,使各项响应满足限值要求。

表1 各项风振响应最不利结果汇集Tab.1 Most unfavorable results of wind response
4 结构的风振响应控制
4.1 控制手段的提出和确定
从1972年Yao[12]首次提出结构振动控制在土木工程中的概念后,应运而生许多结构控制措施,其中就包括质量阻尼器和黏滞阻尼器,截止到目前,这两种控制措施已经被用于国内外许多重大的大型工程中。
质量阻尼器在质量、刚度系数、阻尼比等结构体系调谐参数合理选取的情况下,主结构的振动反应(位移、加速度)最多可衰减30%~60%,可有效衰减主结构在各种外部振动冲击下的振动反应,从而满足结构正常使用要求(见图18的台北101大厦)。
对于黏滞阻尼器的应用研究中,Constantinou等[13]等通过试验手段验证了黏滞阻尼器对于结构的风振响应的控制效果,尤其对于中小强度的风振最为有效。随着黏滞阻尼器理论研究的深入和成熟,世界各国都不断有新的黏滞阻尼器减振工程实例。其中就包括台北101大厦(图18),墨西哥Mayor大厦(图19),波士顿111Huntington大楼,北京银泰中心等。

图18 台北101大厦Fig.18 Taipei 101


图19 墨西哥Torre Mayor大厦Fig.19 Torre Mayor building
因此,参考现有工程,针对该千米高层330°风向角下的位移角极值较大,0°风向角下的扭转响应过大的特点,拟用质量阻尼器和黏滞阻尼器对结构进行风振控制。
4.2 质量阻尼器控制方案及控制结果
4.2.1 质量阻尼器参数确定
在质量阻尼器中,存在多种阻尼器形式,其中调谐质量阻尼器(TMD)和多重调谐质量阻尼器(MTMD)已经在国内外许多实际工程中得到证实,因此本次研究采用TMD和MTMD进行风振控制。
首先介绍TMD的参数计算理论,根据Den Hartog经典参数设计理论,TMD的质量md,刚度kd,阻尼cd可由式(9)计算
(9)
式中:μ是模态质量比,为质量块质量与模态质量的比值,一般为0.005~0.02;M为结构被控振型的模态质量;ωd为TMD的最优自振频率;λ为结构与TMD的频率比;ωn为结构n阶自振圆频率,ξdopt为TMD的最优阻尼比。
TMD的最优阻尼比,TMD的频率比可按式(10)计算
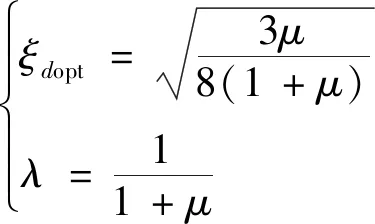
(10)
关于MTMD的模型选择以及参数计算,首先由于频率呈均匀分布的MTMD存在近零最优平均阻尼比,它的存在会使MTMD产生大的冲程,这时的MTMD实际上没有任何实际意义。因此本文采用不存在近零最优平均阻尼比的MTMD模型。
根据文献[14],本文选用的MTMD系统中,每个质量块的自振频率的分布满足图20。

图20 MTMD的中质量块个数与自振频率关系图Fig.20 Relation between the number of mass and the natural frequencies (MTMD)
在图20中,ωT为MTMD系统的平均频率,β为MTMD的频率间隔,n为质量块的个数。根据图20,在对MTMD系统进行参数设计前,需要定义结构要控制振型的频率为ωs,质量块的频率增量为Δω,频率调谐系数f=ωT/ωs,每个质量块的频率比为rj=ωj/ωs,MTMD系统总质量与结构振型质量的比值为μ。
结合图20,可得第j个 TMD的固有频率为
(11)
第j个TMD的阻尼比为
(12)
第j个TMD的质量比为
(13)
在确定了MTMD的个数n及MTMD系统总质量与结构振型质量的比值μ后,MTMD系统的最优频率调谐系数为f,最优平均阻尼比ξT,最优频率间隔β,可参考表2和表3[15]插值选取。
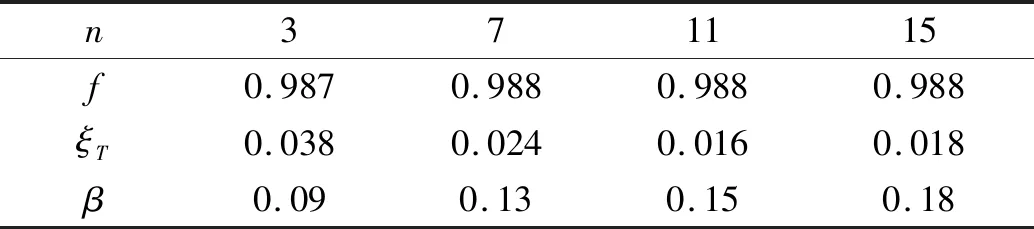
表2 MTMD参数选取(μ=0.01)Tab.2 The parameter of MTMD (μ=0.01)

表3 MTMD参数选取(μ=0.03)Tab.3 The parameter of MTMD(μ=0.01)
4.2.2 质量阻尼器的风振控制方案
根据《建筑结构风振控制技术规范》6.1.2的规定,TMD的质量块宜安放在主体结构的顶层或所控制振型的峰值处。对于超高层建筑结构,一般考虑第1振型对结构响应的贡献就能满足精度要求,所以对于超高层建筑结构,TMD大多设置在结构顶层。由于单个TMD(工况T1、T2)质量过大。尝试将TMD拆分成多个(工况T3),减小对结构的局部荷载,并尽量安放在结构外围,以达到对结构扭转响应的有效控制。根据这一理论,基于TMD的风振控制方案可如表4所示,阻尼器布置示意图如图21所示。
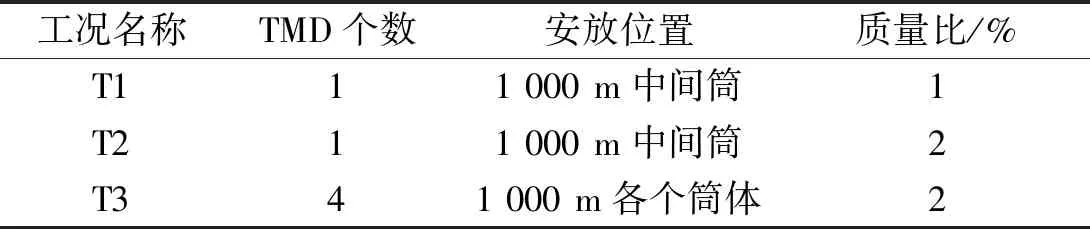
表4 基于TMD的风振控制工况汇总Tab.4 Wind vibration control methods (TMD)
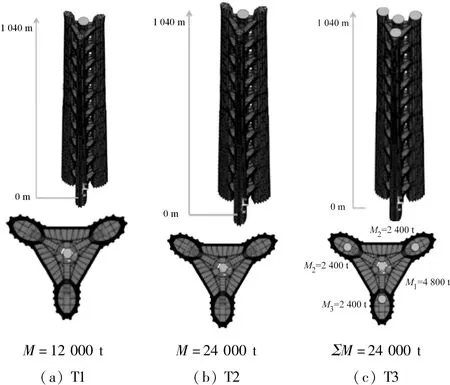
图21 TMD阻尼器布置示意图Fig.21 Schematic diagram of damper arrangement (TMD)
由于在MTMD减振装置的设计中,质量比、安装位置、质量块数量等均会对减振效果产生影响。其中关于MTMD的安放位置,根据《建筑结构风振控制技术规范(征求意见稿)》规定,当控制结构的第1振型风振响应时,宜设置在结构顶部;当结构以多振型振动时,可在结构多个位置安装多个阻尼器,需根据减振要求确定阻尼器的数量和安装位置。因此,为了尽可能的得到最优控制方案,本文综合考虑上述因素,提出如表5所示的六种工况。
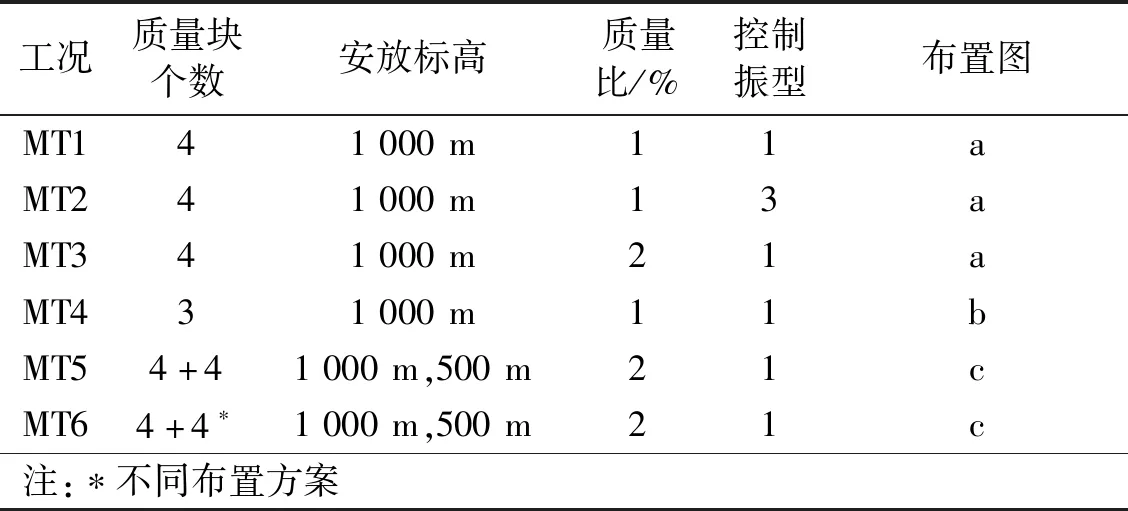
表5 基于MTMD的风振控制工况设置Tab.5 Wind vibration control methods (MTMD)
其中根据风振响应结果,该千米级结构的扭转响应较为明显,而结构的第3阶振型为扭转振型,因此本文参考文献[15-16],设置了一个工况用于控制结构第3阶振型,即工况M2。此外,M3考虑了质量比的影响,M4,M5和M6考虑了质量块个数及摆放位置的影响,其布置图如图22所示。

图22 MTMD阻尼器布置示意图Fig.22 Schematic diagram of damper arrangement (MTMD)
4.2.3 质量阻尼器风振控制结果及分析
为较好的评价控制方法对于结构的控制效果,对于风振控制后的极值风响应,定义控制率ηX为
(14)

采用上文所述的各控制工况对结构进行风振控制分析,得到如表6所示的风振响应控制结果。

表6 基于质量阻尼器的风振控制率结果Tab.6 Wind-vibration control rates based on mass dampers %
从控制效果中可以发现,无论是TMD还是MTMD,整个系统的质量比越大,控制效果越好。但是由于该千米级摩天大楼振型质量较大,考虑到安装制作难度以及结构本身的承载力,质量阻尼器的质量比不宜超过1%。除此之外,两种控制方案中对于扭转角速度均有或多或少的加剧效果,但是均不大于6%。考虑到扭转角速度数值本身就偏小,因此,对于该部分的加剧作用本文认为可以忽略。对比两种质量阻尼器类型对于其他响应的控制效果,本文认为MTMD的控制效果要优于TMD方案。虽然该结构的扭转响应较大,但是在控制参数计算时,依然应该以1阶振型为控制目标。
综上所述,并综合考虑控制效果以及经济和施工技术的影响,本文认为,对于该千米级摩天大楼,可优先选用MTMD的控制方案,在选用合适质量比(<1%)的前提下,集中布置在结构顶部,并且在整个布置平面内保证均匀。
4.3 黏滞阻尼器控制方案及控制结果
4.3.1 黏滞阻尼器参数确定
本文选用的黏滞流体阻尼器是东南大学建筑工程抗震与减震中心与香港理工大学和南京液压机械制造厂等单位合作,研制出的双出杆工程减振黏滞流体阻尼器(如图23)。

图23 双出杆工程减振黏滞流体阻尼器实物图Fig.23 Viscous fluid damper
其阻尼系数Cd=2.5×108N·s/m,速度指数α=1,最大阻尼输出力为2 000 kN,最大行程为100 mm。采用的阻尼器拟采用套索式的安装方式,以最大程度的发挥阻尼器耗能的能量,其放大系数β0可达2.0~4.0,计算时保守采用2.0。
根据《建筑抗震设计规范》(GB 50011—2010)12.3.4条的规定,阻尼器的数量可应用下列公式近似确定。
消能部件附加的有效阻尼比为
(15)
式中:ξa为消能减振结构的附加有效阻尼比;Wc为所有消能部件在结构预期位移下往复一周所消耗的能量;Ws为设置消能部件的结构在预期位移下的总应变能。
不计扭转影响时,消能减振结构在其水平风荷载作用下的总应变能估计为
(16)
式中:Fi为质点i的水平风荷载标准值;ui为质点i对应于水平风荷载标准值的侧移。当考虑扭转时,Fi和ui表示自由度i上的广义荷载与广义力。
单个阻尼器在一个振动周期内,阻尼力方向与振动方向相反,起耗能作用,一个周期间所消耗的能量为
Wci=2·Fci·Ai=2·CiV·ΔU
(17)
式中:Ci为线性黏滞阻尼器i的阻尼系数;V为各层速度的均方差的平均值;ΔU为各层层间侧移的均方根的平均值。
根据式(8)~(10)可以得到阻尼器的总数量。本文参照上述计算公式,得到了结构在各个风向角下的应变能。由表7中的结果可知,结构在330°风向下应变能最大,因此选择此方向应变能进行结构VFD控制参数计算,确定出阻尼器个数范围如表8所示,最后将阻尼器个数验算范围确定为2 000~5 000。

表7 各风向下结构应变能Tab.7 Strain energy under different wind directions

表8 阻尼器数量范围的确定Tab.8 Determination of the number range of dampers
4.3.2 黏滞阻尼器风振控制方案设计
对于黏滞阻尼器的布置,包括平面布置以及立面布置上。对于平面布置,阻尼器应尽量在结构的两个主轴方向布置;在立面布置上,以层间位移为阻尼器竖向布置的控制指标,在层间位移较大的楼层装设阻尼器。
考虑以上布置原则,结合阻尼器的个数,形成了如图24所示的阻尼器平面布置方案,之后结合立面布置原则,最终形成了如图25所示的10种黏滞阻尼器的控制方案。下文将分别采用该10种不同的控制方案对结构进行风振响应控制。

(a)方案A 在结构外框筒及内外框筒连接处布置
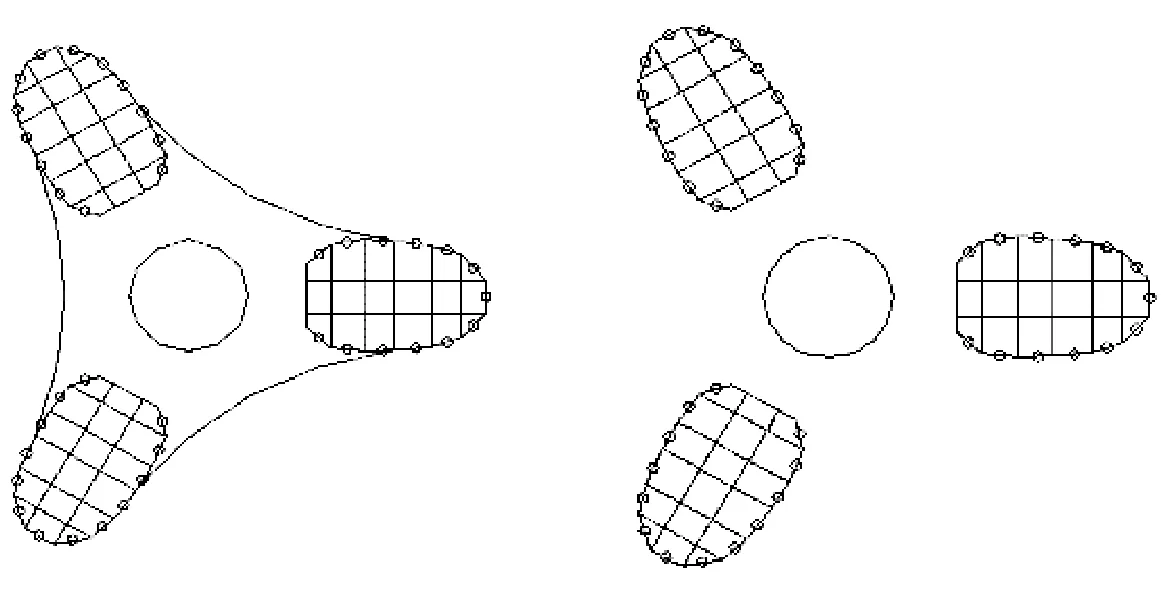
(b)方案B 仅在结构外框筒布置
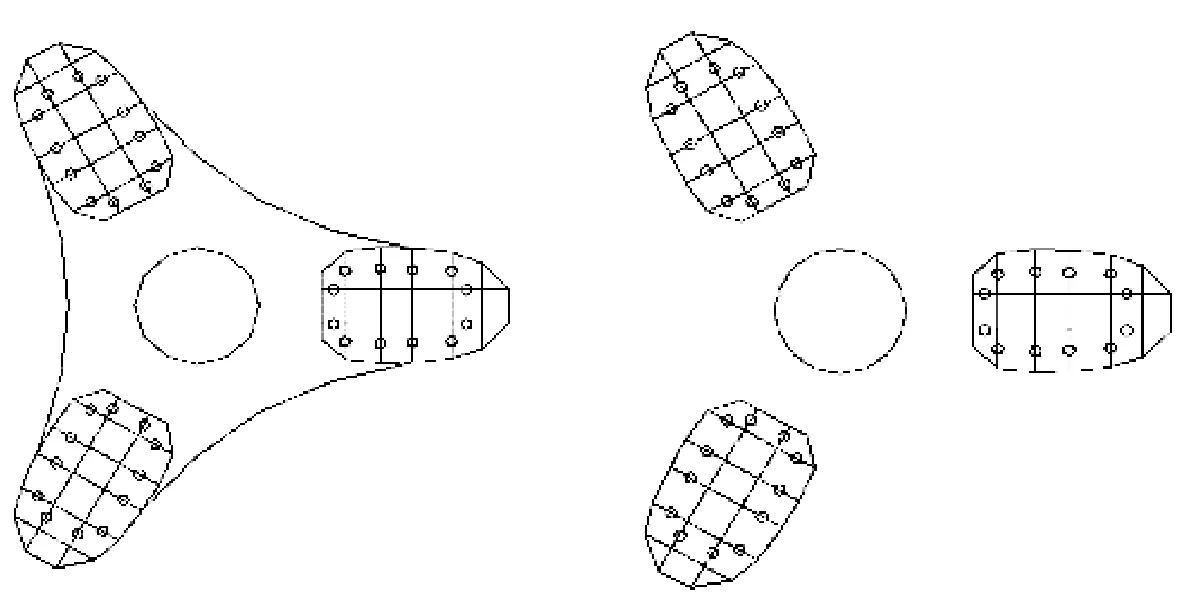
(c)方案C 仅在结构内外框筒连接处布置

图25 工况设置示意图Fig.25 Control method of Viscous fluid damper
4.3.3 黏滞阻尼器风振控制结果及分析
表9给出了黏滞阻尼器控制方案下各控制工况的风振响应控制效果。图26和图27分别给出了阻尼器个数及布置方案对响应控制率的影响。
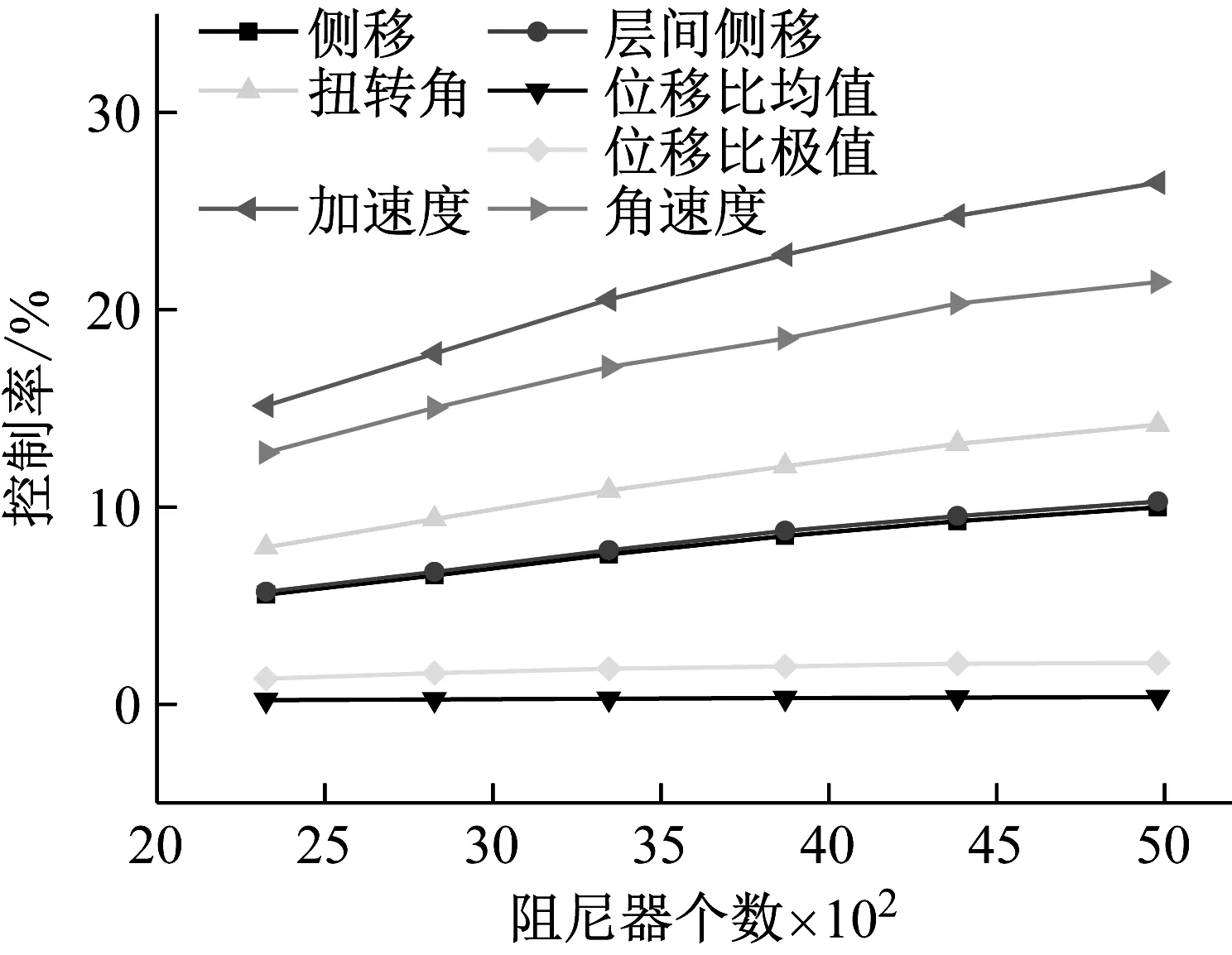
图26 阻尼器个数对响应控制率的影响Fig.26 The influence of the number of dampers
由图表可知,对于该结构,可以选择在外框筒与内外框筒连接处均布置阻尼器,对结构的侧移和扭转响应进行控制。在计算阻尼器个数时,结构应变能建议按极值响应进行计算。

表9 基于黏滞阻尼器的风振控制率结果Tab.9 Wind-vibration control rates based on viscous fluid damper %

图27 布置方案对响应控制率的影响Fig.27 The influence of the arrangement of dampers
5 结 论
本文通过对一个拟建的千米级摩天大楼进行风振响应分析,针对响应结果分别采用质量阻尼器以及黏滞阻尼器进行了风振控制研究,得到了如下的相关结论:
(1)该千米级超高层结构在设计风荷载下的风振响应分析表明,330°为结构的侧移最不利风向,0°为结构的扭转最不利风向。结构的各种响应中,各层侧移、加速度满足要求,层间侧移角、位移比极值略超限值要求,需要进行振动控制;
(2)对于该千米级超高层结构,当采用质量阻尼器(TMD和MTMD)进行风振控制时,可以将结构要控制振型选定为1阶振型,采用本文的设计方法,采用MTMD对结构进行控制。在参数计算时,应对比考虑质量比和控制效率。对于本文的千米级摩天大楼,质量比<1%较为合适。对于质量块的安放位置,不建议分层安放,可集中布置在结构顶部,并均匀布置在整个平面内。
(3)当采用黏滞阻尼器对类似本文的框架-核心筒结构进行风振控制时,可以选择在外框筒与内外框筒连接处均布置阻尼器。在阻尼器参数计算时,建议按结构的极值响应进行结构应变能的计算。

