火灾后钢管RPC柱抗爆动力响应数值模拟研究

邹慧辉，陈万祥，郭志昆，周子欣

(1.陆军工程大学 爆炸冲击防灾减灾国家重点实验室，南京 210007;2.中山大学 土木工程学院，广州 510275)

近年来世界范围内火灾和爆炸事故频发，火灾后工程结构抗冲击爆炸性能已引起国际防护工程界的极大关注[1-2]。为提高工程结构抗火及抗爆性能，工程界正致力于开发新材料和新结构。活性粉末混凝土(Reactive Powder Concrete，RPC)是一种高强度、高韧性、低孔隙率的超高性能混凝土[3]，自1997年提出以来就受到了国内外学者的广泛关注，并已在桥梁、铁路、军事等诸多领域得到广泛应用[4]。2015年2月我国针对RPC发布了国家标准GB/T 31387—2015《活性粉末混凝土》[5]，为RPC的进一步研究和推广应用提供了规范。然而，随着混凝土强度的提高，脆性变得越来越明显，在一定程度上限制了其工程应用，钢管混凝土的出现极大地改善了混凝土的工作性能[6]。钢管活性粉末混凝土(Reactive Powder Concrete-Filled Steel Tube，钢管RPC)不仅具有钢管混凝土的一般优点，经济效益更为显著，且具有极高的抗压强度和抗冲击韧性[7]，是一种极具开发潜质和应用前景的新型抗火抗爆组合结构。

研究发现，RPC的耐火性差、脆性明显，将RPC灌入钢管中形成钢管RPC结构，能有效防止其高温爆裂，同时由于钢管的约束作用，提高了RPC的强度和变形性能，使RPC材料的优异性能得以充分发挥。目前，对钢管RPC在常温下的基本力学性能研究较多[8-10]，但对火灾或爆炸作用下动态行为的研究较少。近年来，冯红波等[11-12]通过试验研究和数值模拟的方法对方钢管混凝土柱、圆钢管混凝土柱和复式钢管混凝土柱的抗爆性能和破坏模式进行了分析，到了爆炸折合距离和结构形式对动力响应的影响。李国强等[13]进行了12根钢管混凝土柱的现场抗爆试验，研究了轴压比、炸药当量、含钢率和混凝土强度等多个因素对钢管混凝土柱抗爆性能的影响。王宏伟等[14]进行了4根方钢管混凝土柱和4根圆钢管混凝土柱的足尺爆炸试验，对其中挠跨比小于1/100的4根钢管混凝土柱开展了残余承载力试验，并对损失程度进行评估。Zhang等[15-16]开展了CFST柱的近距离抗爆试验，研究表明CFST柱的抗爆性能良好，通过有限元法成功模拟了抗爆试验结果，并通过分析认为核心混凝土可以有效抑制钢管的局部变形。邹慧辉等[17]开展了4根火灾后钢管RPC柱的抗爆性能试验，分析了不同受火时间和比例距离对火灾后钢管RPC柱抗爆性能的影响。

本文利用非线性有限元软件LS-DYNA对火灾后钢管RPC柱在爆炸荷载作用下的动力响应及破坏形态进行数值分析，研究荷载参数、几何特征、材料性能等因素对抗爆动力响应的影响，从而为火灾后钢管RPC的抗爆设计计算提供理论依据。

1 爆炸荷载作用下钢管RPC柱有限元模型

1.1 材料模型

由于钢材在升温和冷却过程中其力学性能具有较好的恢复能力。根据Yang等[18]的研究结论，高温后作用的钢管本构模型可取常温条件下的本构模型，高温后混凝土芯柱的力学性能只与最高过火温度有关，与升降温过程关系不大。因而，高温后混凝土芯柱的应力-应变关系与常温条件下一致，但峰值应力和峰值应变需要考虑最高过火温度的影响进行适当修正。因此，本文继续沿用常温条件下钢材和混凝土的本构模型，而对经历高温后的材料力学性能参数进行修正。

1.1.1 钢材

钢管采用*MAT_PlASTIC_KINEMATIC弹塑性模型[19]，该模型考虑了包辛格效应和应变率效应，能够准确、高效地模拟钢材的力学性能。屈服应力表达式为

(1)

(2)

式中，E为材料弹性模量；Etan为硬化模量。

常温下钢材的基本力学性能参数如表1所示。

表1 钢管的材料参数Tab.1 Material parameters of steel tubulr

高温后钢材屈服强度的表达式为[20]

(3)

式中:fy为钢材常温下的屈服强度；fy(T)为钢材高温后的屈服强度；T为钢材经历的最高温度。

高温后钢管的弹性模量的表达式为

20 °C≤T≤900 °C

(4)

式中:Es为钢材常温下的弹性模量；Es(T)为钢材高温后的弹性模量。

1.1.2 RPC

任意状态下的强度面在三个给定的强度面之间迁移，并满足下面的关系

Δσ=η(λ)(Δσm-Δσmin)+Δσmin

(5)

式中:0≤η(λ)≤1为迁移函数；Δσm为极限强度面；Δσmin为屈服面Δσy或残余强度面Δσr。极限强度面、残余强度面及软化强度面的偏应力与对应静水压力的关系分别为

(6)

(7)

Δσr=a0f+p/(a1f+a2fp)

(8)

式中:p为静水压力；fc和T分别为材料的单轴抗压强度和单轴抗拉强度；fyc=0.45fc；ai，aiy，aif(i=1,2,3)为屈服面特征常数；λ为损伤变量；λm为极限损伤变量；ψ为拉压子午线的比例系数。

高温后RPC的强度取值为[21]

(9)

式中，fc(T)为高温后混凝土的强度。

1.2 有限元模型的建立

模拟工况为文献[17]的试验工况。钢管RPC柱尺寸为2 500 mm×194 mm×6 mm，炸药距柱中间上表面的垂直距离1 500 mm处，分析模型如图1(a)所示。由于荷载及结构的对称性，取四分之一模型进行分析(如图1(b))。

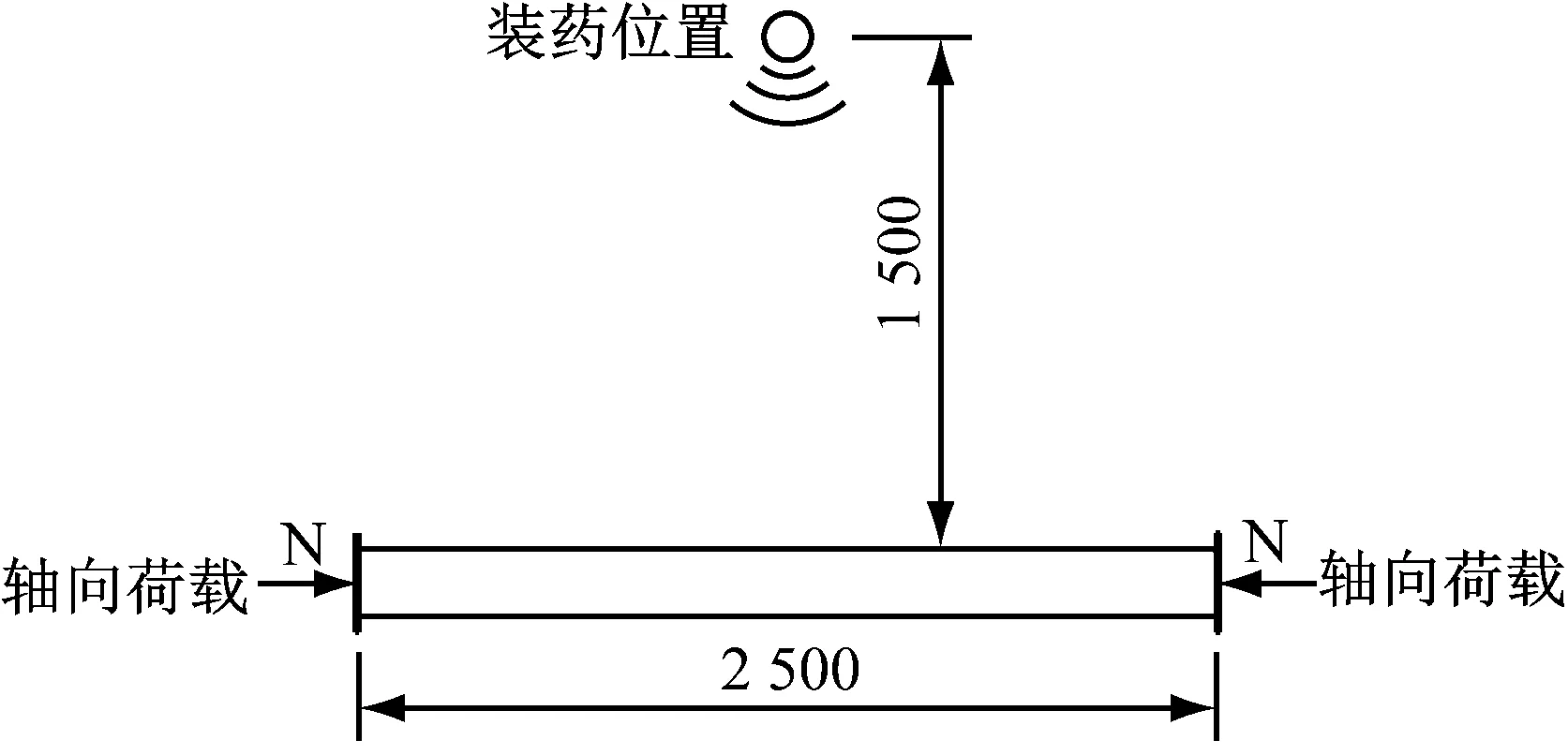
(a)分析模型

(b)1/4有限元模型图1 分析模型示意图Fig.1 Analysis model diagram

1.2.1 火灾后截面温度场的分层模型

在项目施工阶段承包方工程造价控制，主要是以工程承包合同为依据，进行施工组织结构的设计。依据工程量计量数据，严格依据现场签证进行工程变更及索赔申请，保证工程造价的有效控制。在具体项目施工造价工程环节，承包方可依据工程量清单计价的相关内容，结合前期标准设计方案，根据项目特点进行项目分组，针对某个关键分量进行审核，通过不同分量之间的联系，判定其他分部工程造价控制的准确性。

ISO-834标准火灾后钢管RPC截面所经历的最高温度可以通过ANSYS数值模拟方法得到，钢材和RPC的热工参数取值表2所示。

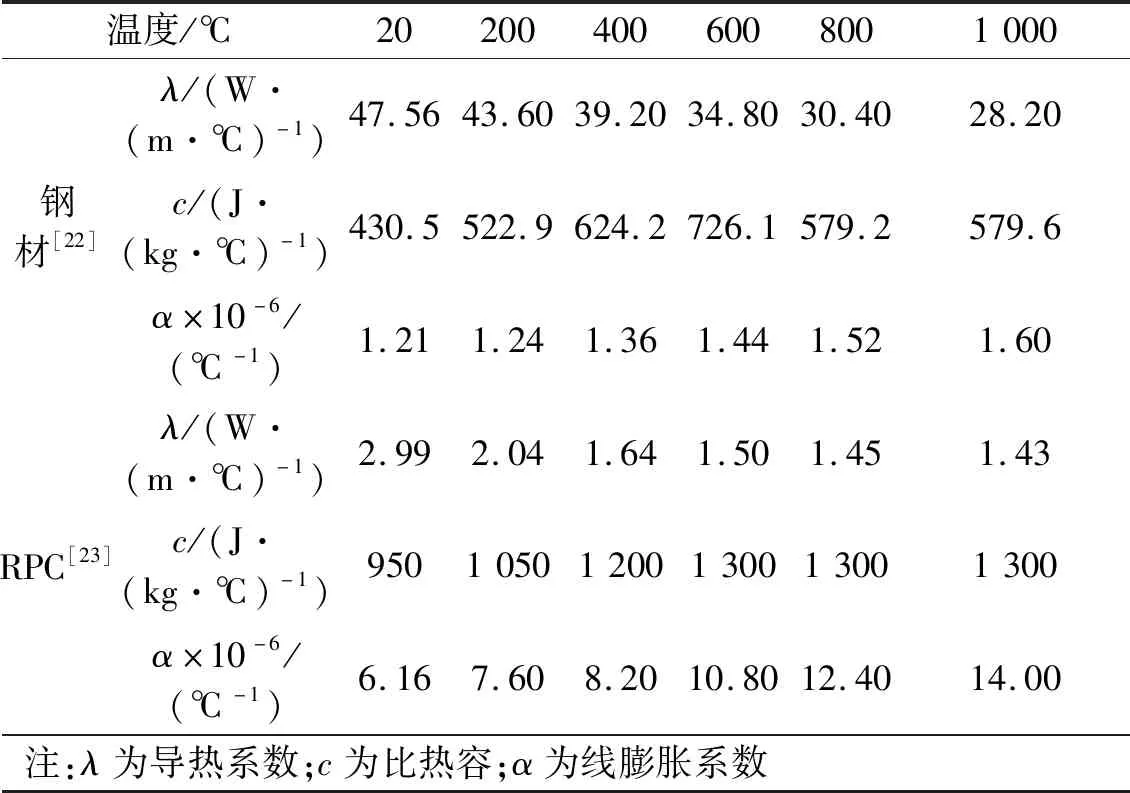
表2 材料的热工性能参数Tab.2 Thermal performance parameters of material

以受火60 min的钢管RPC为例，其截面温度场如图2所示。钢管壁厚较薄，导热性能较好，其截面温度梯度较小，可认为其温度均匀分布；而RPC需要考虑不均匀的温度场。文献[24]采用精细的有限元模型，考虑最高温度对每一单元材料模型的影响，既先计算温度场，之后重新进入前处理，在温度场分析之后，转入力学分析，并将相应的热分析单元转化为相应的力学分析单元，读入热分析中材料属性。这一种方法可以较精确的反映每一单元所经历的温度，但建模、计算工作量较大。本文根据温度场的分析结果，采用如图3(b)所示的条带划分法[25]建立分层模型，每一条带内的单元材料性能相同。温度场分布越均匀、条带数目越多，按条带法原理计算的精度就越高。由于材料高温后力学性能随温度变化的经验公式(9)是根据温度段拟合的，对计算钢管混凝土强度而言，一般三条就能达到足够的精度。因此，本文采用的分层模型具有相对较高的计算效率和精度。

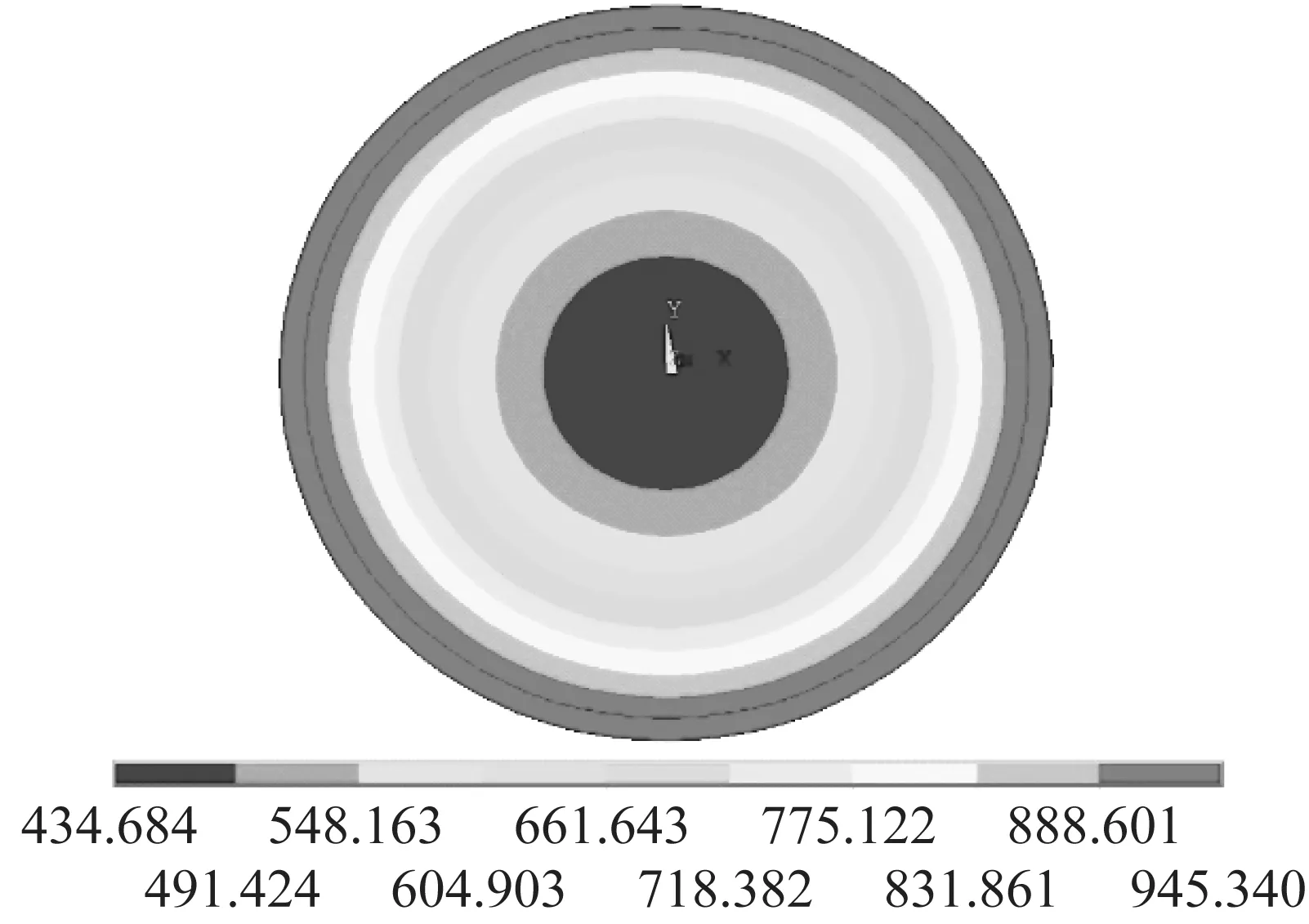
图2 钢管RPC柱横截面温度场Fig.2 Temperature gradient of cross-sectional of RPC-FSTC

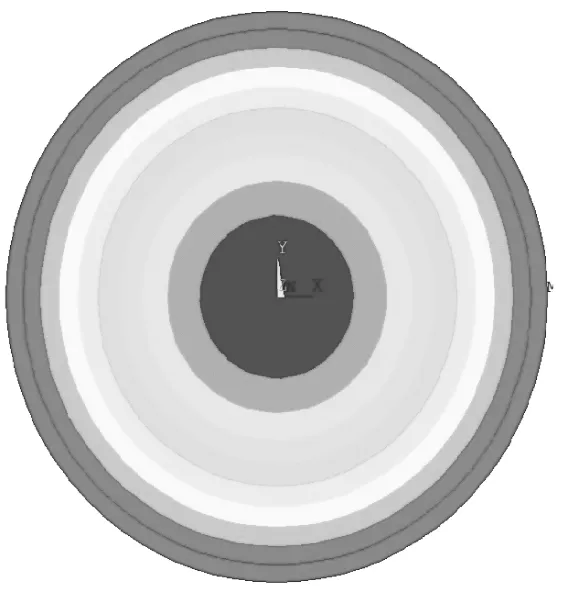
(a)精细模型

(b)分层模型图3 截面温度场的不同模型Fig.3 Different models of cross-section temperature gradient

1.2.2 有限元模型

有限元模型使用ANSYS13.0进行前处理，钢管和RPC均采用8节点实体单元solid164进行离散。文献[15]的研究指出，有限元网格尺寸为20 mm左右时，钢管混凝土柱的抗爆数值模拟具有较好的准确性和高效性。本文采用的网格尺寸平均为20 mm，网格划分采用映射法，不同受火时间划分后的网络模型如图4所示。试件两端采用200 mm×200 mm×15 mm的钢板约束柱端的上下位移，以模拟试验中的边界条件。钢板与柱端采用自动单面接触算法。钢管与RPC之间的接触采用LS-DYNA中的自动面面接触(TDSS)。

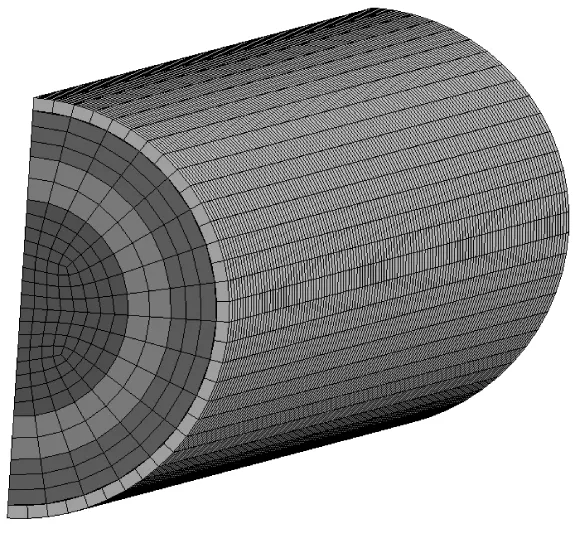
(a)受火60 min

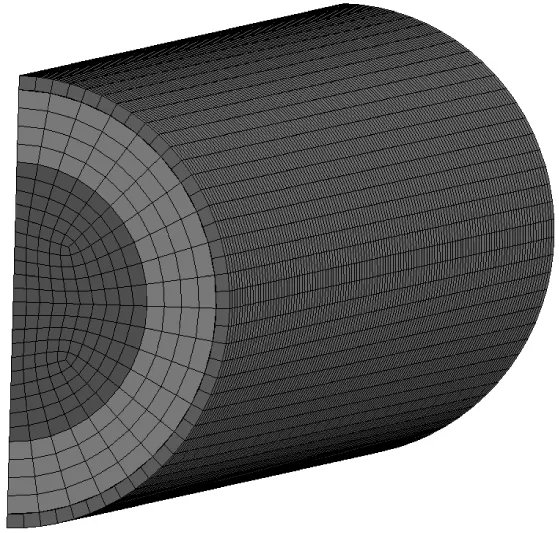
(b)受火90 min

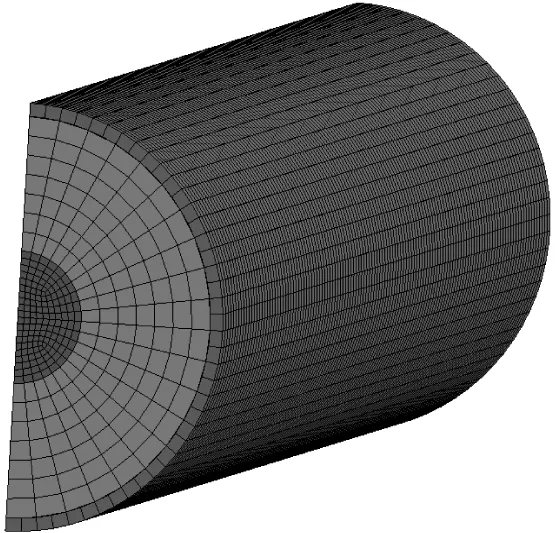
(c)受火105 min图4 有限元网格模型Fig.4 Finite element mesh model

1.2.3 爆炸荷载的模拟

数值模拟分两步进行：第一步，采用动力松弛法对柱施加轴向力作用，以模拟柱子轴向荷载作用；第二步，待恒定轴向力稳定后施加爆炸荷载，进行瞬态分析。爆炸荷载采用LS-DYNA中的*LOAD_BLAST_ENHANCED命令进行施加，该方法加入了爆炸波入射角的影响，使用范围较广，适用于各种远近及超远距离的结构和构件的动态响应分析。

图5 荷载施加示意图Fig.5 Load application diagram

1.3 数值模拟结果的验证

图6为柱中位移的数值模拟时程曲线和试验位移时程曲线对比。从图中可以看出，数值模拟得到的动态位移响应曲线和试验结果基本一致。数值模拟给出的最大位移较试验结果偏小，主要是因为试验中在距爆心较近的区域内结构同时受到爆轰产物和空气冲击波的作用，而在数值模拟中只考虑了空气冲击波对结构的作用。表3为四种工况下数值模拟和试验最大位移的对比，误差均在20%左右，对于近距离爆炸尚在可接受的范围内。

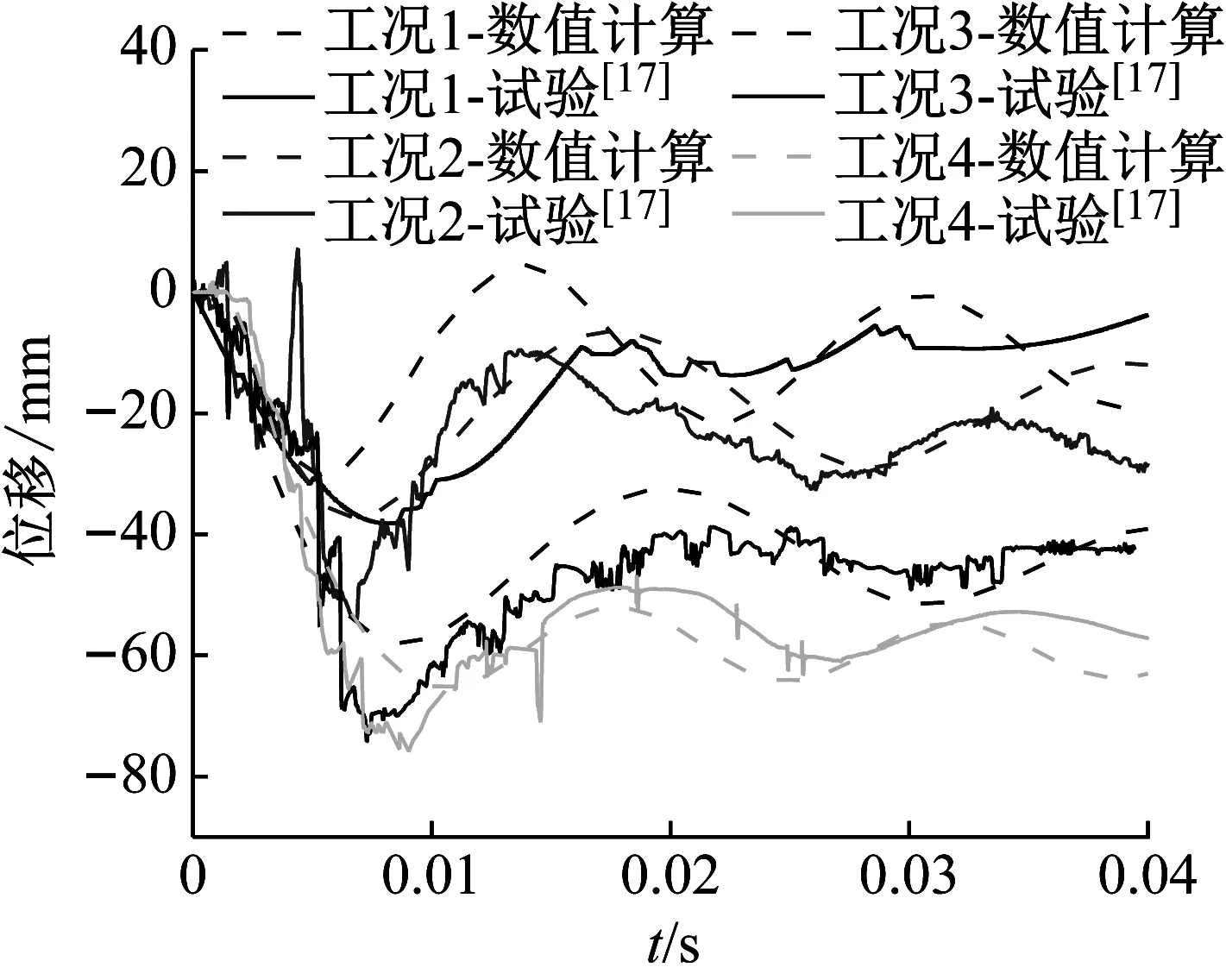
图6 动力响应的数值模拟与试验结果对比Fig.6 Comparison of numerical simulation and test results of dynamic response

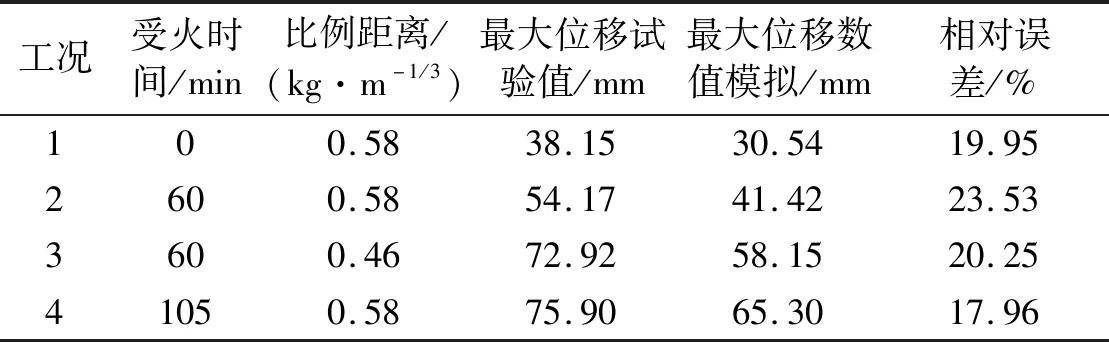
表3 数值模拟与试验结果对比Tab.3 Numerical simulation and test results

2 参数分析

2.1 参数方案设计

由于爆炸试验成本高，不利于大量研究，故采用数值模拟方法进行参数化分析，主要研究荷载参数(受火时间、爆炸荷载、轴向荷载)，几何特征参数(钢管壁厚、长径比)，材料性能参数(钢管强度)等因素对火灾后钢管RPC柱动力响应的影响规律。根据正交试验设计方法，参数化分析工况如表4所示。标准工况为受火时间60 min、比例距离1.0 kg/m1/3、轴向荷载1 500 kN、几何尺寸2 500 mm×194 mm×6 mm和钢管屈服强度350 MPa。分析特定参数影响时，保持标准工况中的其他参数不变。

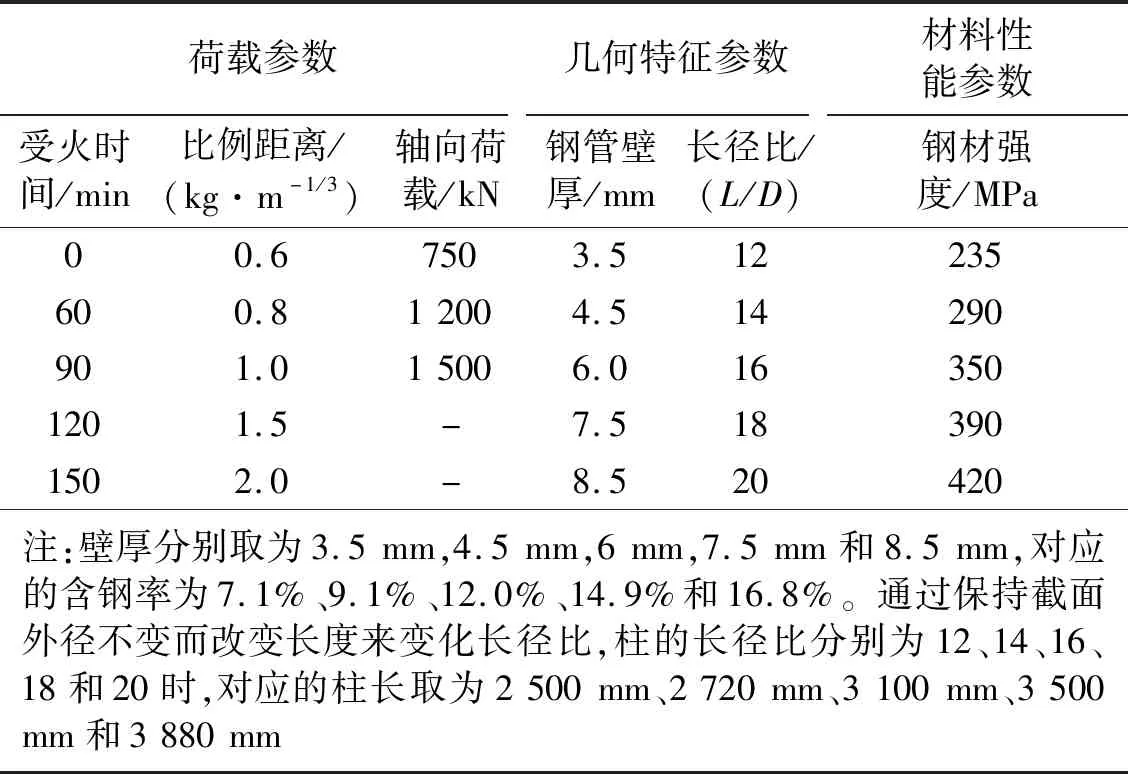
表4 参数分析工况表Tab.4 Parametric analysis table

爆炸荷载作用在柱上的分布规律同炸药起爆中心距构件表面的距离有关，为获得作用在构件表面的均布荷载，在使用关键字*LOAD_BLAST _ENHANCED命令时将炸药坐标设在距构件跨度2倍以外的5 m处。

2.2 结果分析

2.2.1 荷载参数

(1)受火时间的影响。图7为不同受火时间后柱中点位移时程曲线。从图中可以看出，随着受火时间的增加钢管RPC柱的自振频率略有减小，说明高温后钢管RPC刚度裂化，弹性恢复能力有所下降；受火60 min后的曲线最大位移变化幅度同未受火的最大位移变化幅度相当，随着受火时间的继续增加，位移弹性恢复能力减弱，表明受火时间超过90 min后钢管RPC柱的弹性变形能力进一步减弱。图7为最大位移随受火时间的变化关系曲线，从图中可以看出，最大位移随着受火时间的增加而增加。综合以上分析可知，受火时间对钢管RPC柱损伤较大，超过一定时间后损伤严重，抗爆性能显著降低。

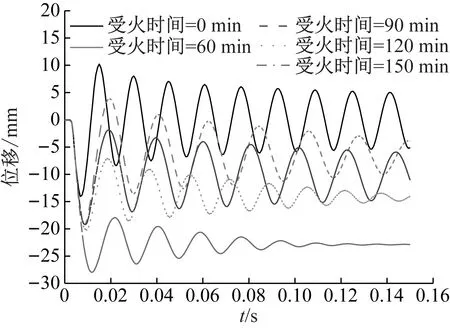
图7 不同受火时间后柱中点位移时程曲线Fig.7 Time history of the displacement of the midpoint of the column after different fire times

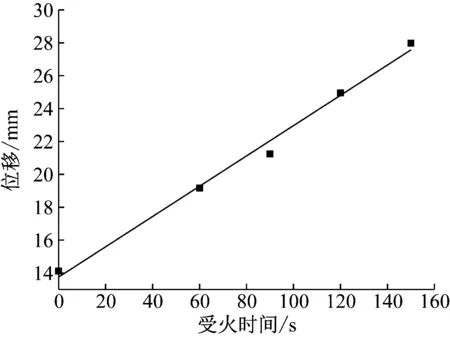
图8 最大位移与受火时间关系Fig.8 Relation between maximum displacement and fire time

(2)比例距离的影响。图9为不同比例距离下柱中点最大位移时程曲线。从图中可以看出，随着比例距离的减小钢管RPC柱的最大位移显著增加。比例距离为1.5 m/kg1/3和2.0 m/kg1/3时钢管RPC柱基本保持弹性变形，比例距离为1.0 m/kg1/3时最大位移为19.2 mm，但仍有较大的恢复能力；当比例距离为0.8 m/kg1/3时，最大位移明显增大，且恢复位移较小，表明在比例距离为0.8 m/kg1/3时钢管RPC有较大损伤破坏；当比例距离达到0.6 m/kg1/3时最大位移达到80 mm，且恢复值较小。图10为爆炸荷载作用下最大位移随比例距离的变化关系曲线，跨中最大位移随着比例距离的减小而增大。

图9 不同比例距离下跨中点位移时程曲线Fig.9 Time history curve of midpoint displacement at different scale distances

(3)轴向荷载的影响。图11为不同轴向荷载下柱中点最大位移时程曲线。从图中可以看出，随着轴向荷载的增大钢管RPC柱的振动频率减小，但变化不显著；轴向荷载为754 kN时，最大位移为17.6 mm；轴向荷载为1 200 kN时，最大位移为18.2 mm；轴向荷载为1 500 kN时，最大位移为19.2 mm；最大位移随轴向荷载的增加而增大。图12为最大位移随轴向荷载的变化关系曲线，曲线表明承载力范围内的轴向荷载对影响不大。

图10 最大位移与比例距离的关系Fig.10 Relation between maximum displacement and scale distances

图11 不同轴向荷载下柱中点位移时程曲线Fig.11 Time history curve of the midpoint displacement of the column under different axial loads

图12 最大位移与轴向荷载的关系Fig.12 Relation between maximum displacement and axial load

2.2.2 几何特征参数

(1)钢管壁厚(含钢率)的影响。图13为不同钢管壁厚下柱中点最大位移时程曲线。从图中可以看出，随着钢管壁厚的增加钢管RPC柱的振动频率增大，柱的弹性恢复能力增强。当钢管壁厚为3.5 mm时(含钢率为7.1%)，柱的弹性恢复能力较弱，位移时程曲线迅速衰减，且有较大残余位移，表明钢管RPC柱发生了明显的塑性变形；但钢管壁厚大于6 mm时(含钢率为12.0%)，柱均有较好的弹性恢复能力，钢管壁厚为8.5 mm时，柱中动位移处于弹性范围内图14为最大位移随钢管壁厚的变化关系曲线，从图中可以看出，最大位移随着钢管壁厚(含钢率)的增加而基本成线性减小的趋势。

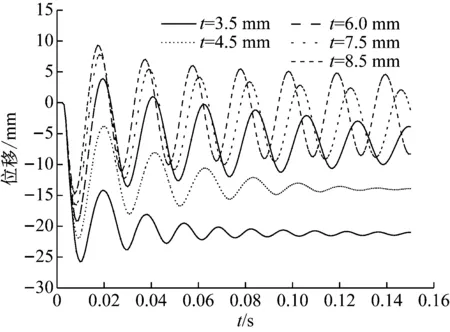
图13 不同钢管壁厚时柱中点位移时程曲线Fig.13 Time history curve of midpoint displacement of different thickness of steel tube

图14 最大位移与钢管壁厚的关系Fig.14 Relation between maximum displacement and thickness of steel tube

(2)长径比的影响。图15为不同长径比下柱中点最大位移时程曲线。从图中可以看出，随着长径比的增大钢管RPC柱的振动频率减小，柱的弹性恢复能力减小。当长径比大于18时，柱的第二个位移峰值大于第一个位移峰值，位移时程曲线有发散的趋势，表明柱有失稳的趋势，但由于荷载作用时间短，最大位移将最终衰减。从图中还可以看出，随着长径比的增大柱中最大位移增加；当长径比为16时，最大位移明显增大；当长径比为18时，最大位移达到45 mm，较长径比为12时增加50%；当长径比为20时，最大位移达到60 mm，较长径比为12时增加50%。图16为最大位移随长径比变化的关系曲线。

2.2.3 材料参数

图17为钢材屈服强度为235～420 MPa时的柱中点最大位移时程曲线。从图中可以看出，钢管RPC柱的振动频率随钢材强度增大的变化并不明显，但弹性恢复能力随钢材强度的增大较为显著；当钢材强度大于350 MPa时，钢管RPC柱会发生明显的反向位移，且柱基本处于弹性范围；从图中还可以看出，随着钢材屈服强度的增加，跨中最大位移减小，但钢材强度增大185 MPa，最大位移仅减小2.4 mm，变化不显著。图18为最大位移随钢材强度变化的关系曲线。

图15 不同长径比时柱跨中点位移时程曲线Fig.15 Time history curve of midpoint displacement at different length to diameter ratio

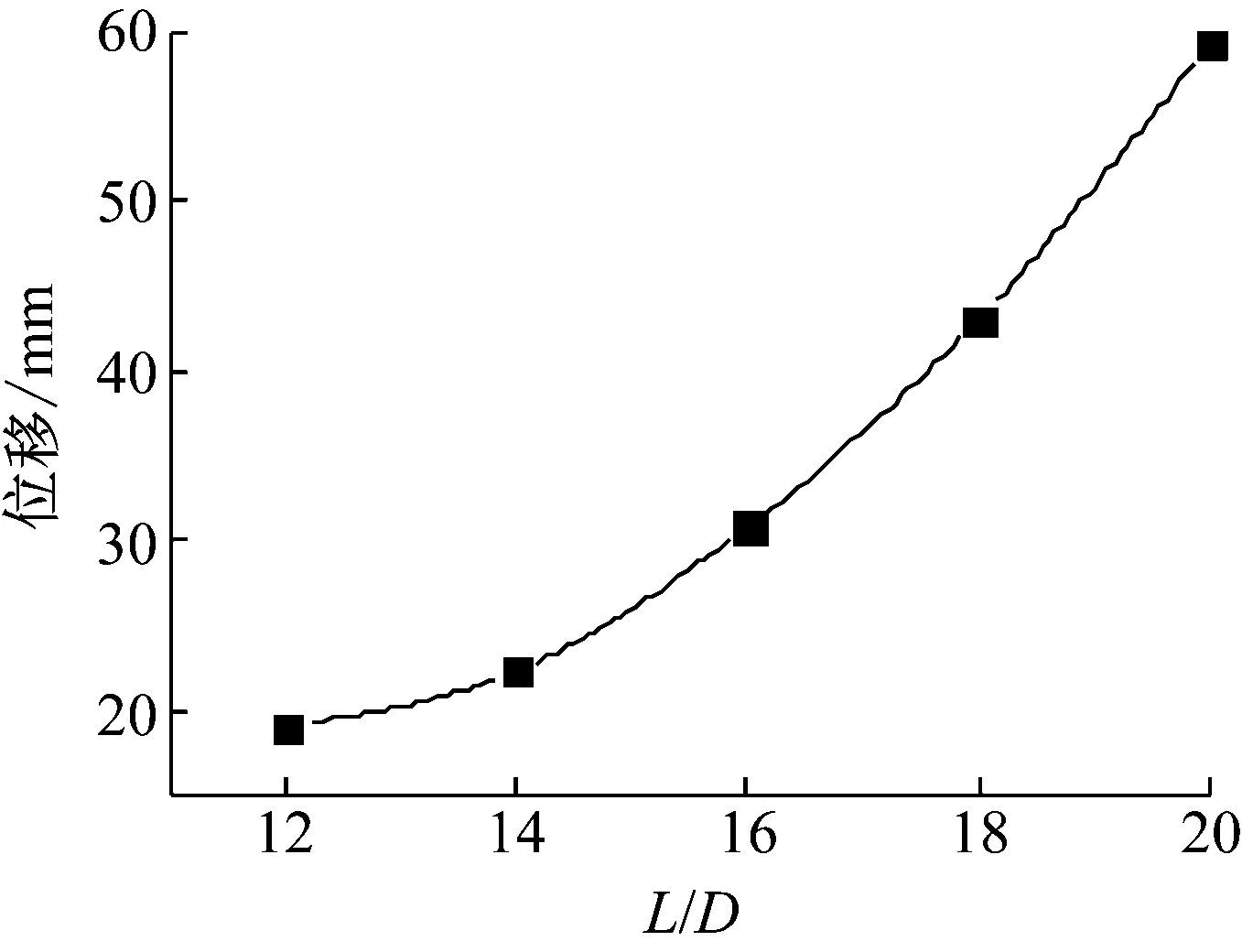
图16 最大位移与长径比的关系Fig.16 Relation between maximum displacement and length to diameter ratio

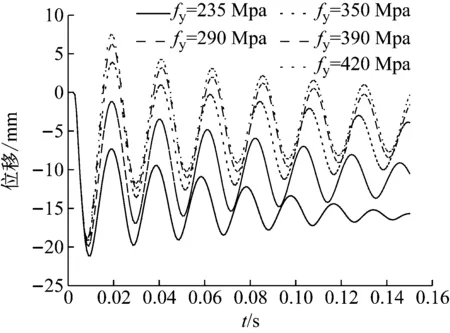
图17 不同钢材强度时跨中点位移时程曲线Fig.17 Time history curve of midpoint displacement at different steel strengths

3 抗爆性能分析

3.1 钢管RPC柱的破坏形态

爆炸荷载作用下钢筋混凝土梁、板、柱都有弯曲、弯剪、直剪破坏三种典型的破坏形态[26]，一些学者通过数值模拟也发现在钢管混凝土柱中也有存在类似的三种破坏形态[27]。结构的破坏形态与结构所承受的爆炸荷载特点(荷载峰值、作用时间、荷载分布规律等)和结构构件特性(截面抗力、长径比等)均有关系。根据上述参数分析的结果可知，比例距离、受火时间、长径比三个因素对柱的动力响应影响较大，下面分析这三个参数对火灾后钢管RPC柱破坏形态的影响。

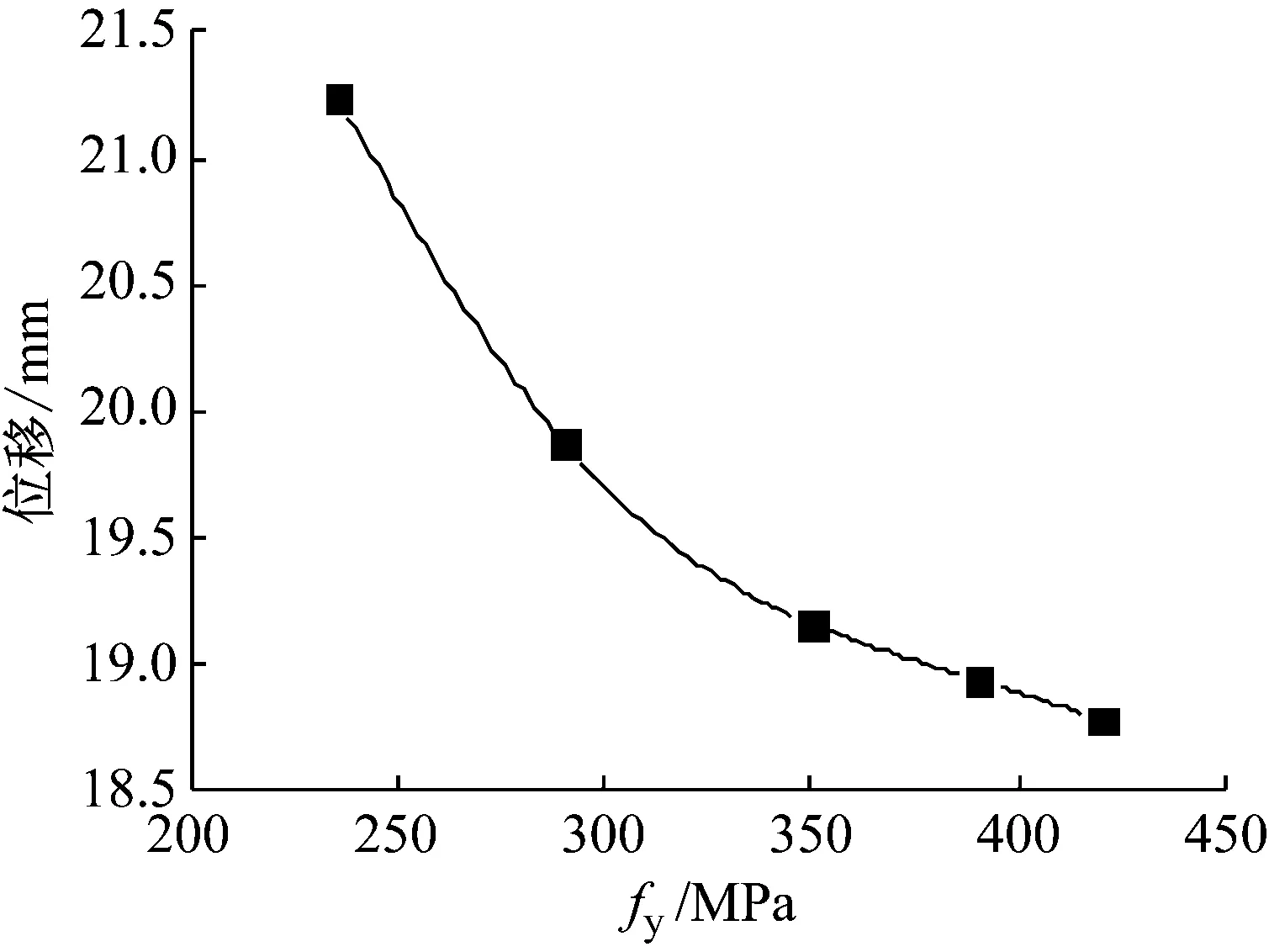
图18 最大位移与钢材强度的关系Fig.18 Relation between maximum displacement and steel strength

3.1.1 比例距离的影响

图19(a)～(c)为不同比例距离下柱的破坏形态(损伤云图)。从图中可以看出，在比例距离为1 m/kg1/3时，柱以整体弯曲变形为主，并且弯曲程度不大，表明受火后的钢管RPC柱仍具有较好的抗爆性能；在比例距离为0.8 m/kg1/3时，柱仍以整体弯曲变形为主，在跨中有一定程度的局部变形，同时柱中RPC出现明显塑性区，柱端附近也出现塑性区；在比例距离为0.6 m/kg1/3时，柱跨中出现较为明显的塑性铰，并且塑性区域逐渐扩大，同时柱端附近均出现被直剪和斜剪的破坏趋势。这表明，随着比例距离的增大，火灾后钢管RPC柱出现由弯曲破坏向弯剪破坏的趋势，而由于钢管良好的韧性，其直剪破坏表现为柱端的剪切破坏。

(a)1.0 kg/m1/3

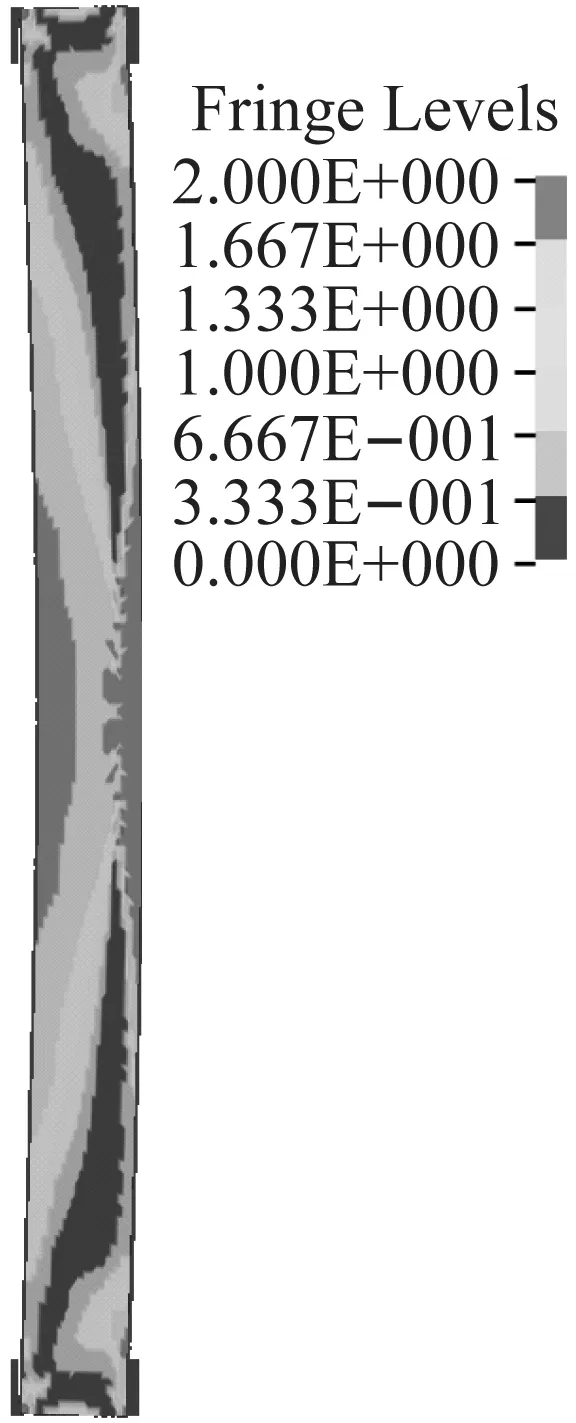
(b)0.8 kg/m1/3

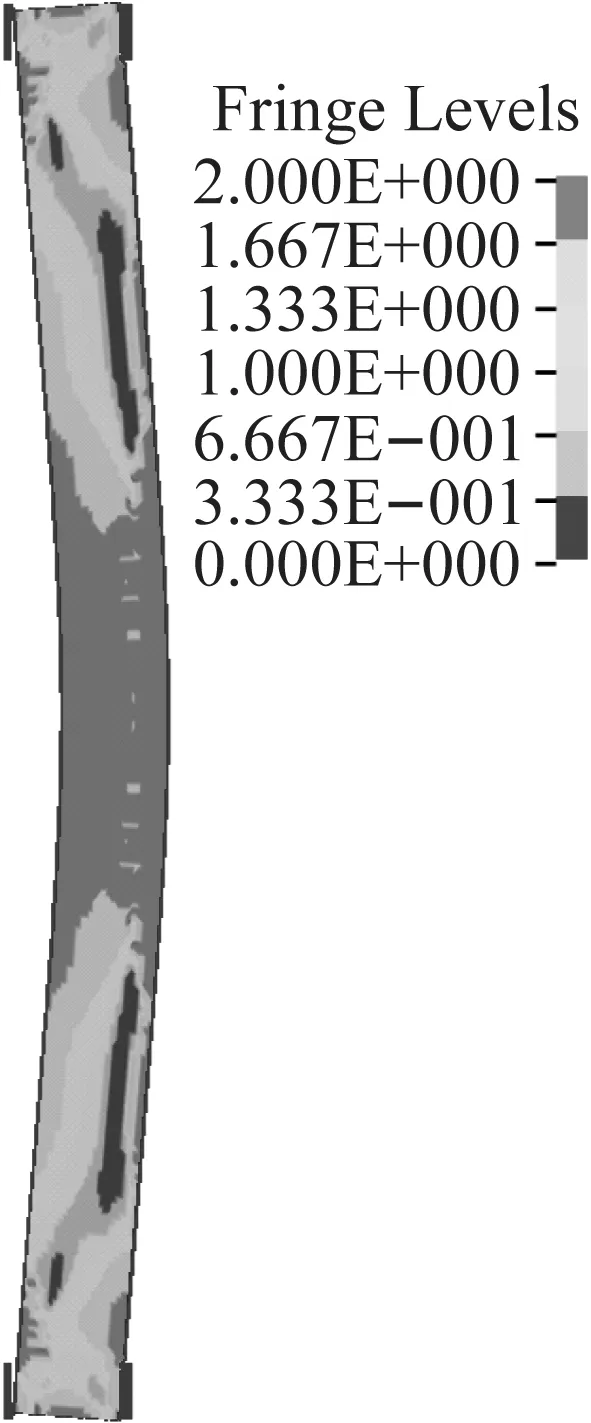
(c)0.6 kg/m1/3图19 不同比例距离下的破坏形态(受火时间为60 min)Fig.19 Failure mode at different scale distances

3.1.2 受火时间的影响

图20为在比例距离为1 m/kg1/3时，不同受火时间后柱的破坏形态。柱均以整体弯曲变形为主，且变形程度不大，表现出较好的抗爆性能。

(a)受火时间60min(b)受火时间90min(c)受火时间120min图20 不同受火时间下的破坏形态(比例距离为1.0 kg/m1/3)Fig.20 Failure mode at different fire time

图21(a)～(c)在比例距离为0.6 m/kg1/3时，不同受火时间后柱的破坏形态(损伤云图)。在图示的三个受火时间后，柱跨中均出现较为明显的塑性铰，并且随着受火时间的增加，柱中和柱端附近的塑性区域逐渐扩大。这表明，随着受火时间的增加，钢管RPC柱抵抗弯曲变形和剪切变形的能力均进一步减弱，但由于温度不均匀分布对抗弯能力的影响更大，从而使得火灾后钢管RPC柱表现出较好的抗剪能力，柱仍表现为弯曲破坏和弯剪破坏。

(a)受火时间60min(b)受火时间90min(c)受火时间120min图21 不同受火时间下的破坏形态(比例距离为0.6 kg/m1/3)Fig.21 Failure mode at different fire time

3.1.3 长径比的影响

图22(a)～(c)为不同长径比的柱在受火时间为60 min、比例距离为1 m/kg1/3时的破坏形态(损伤云图)。柱均以整体弯曲变形为主，柱中均有一定的塑性区，随着长径比的增大，柱的弯曲程度越来越明显，并且在柱中和柱端的塑性区逐渐扩大。在长径比小于20时，柱虽均以整体弯曲变形为主，但随着长径比的增大，柱的跨中位移会急剧增加，并出现较大的残余变形，而不适合继续承载。

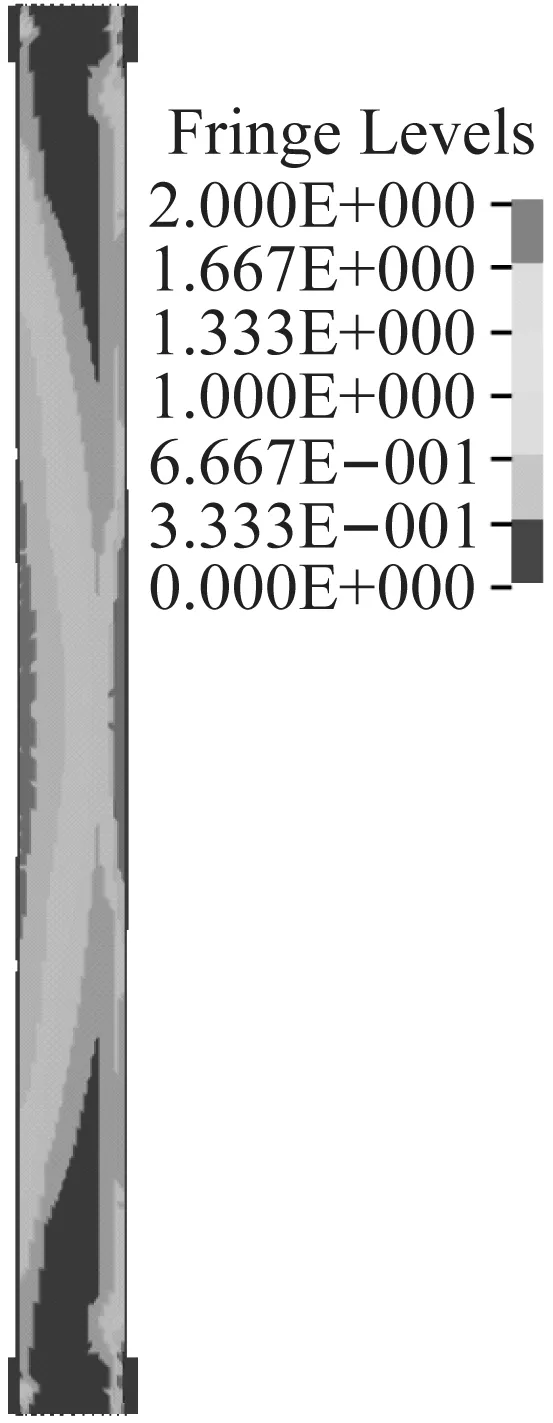
(a)L/D=12

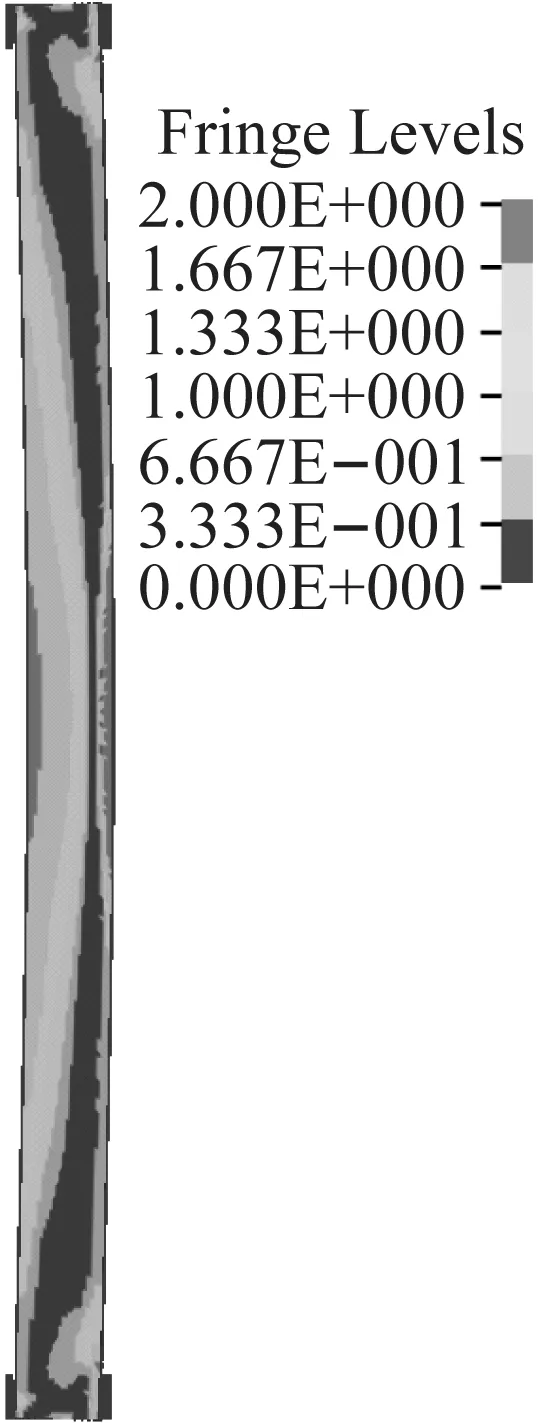
(b)L/D=16

(c)L/D=20图22 不同长径比下的破坏形态(受火时间为60 min)Fig.22 Failure mode at different length to diameter ratio

3.2 火灾后钢管RPC柱的变形能力

钢管混凝土柱在爆炸荷载作用下良好抗爆性能的关键仍在于二者之间的相互作用。若为空钢管，则钢管会由于缺少横向支撑，而在爆炸荷载作用下迅速发生明显的屈曲破坏；混凝土若没有钢管的约束，也会发生严重的断裂破坏。由于二者之间的相互作用，钢管混凝土柱在爆炸荷载的作用下表现出良好的变形和耗能能力。

火灾后钢管RPC柱形成不均匀温度场，强度和刚度均有不同程度下降。但钢管混凝土的几何关系并没有改变，保持良好整体性，钢管混凝土的两个基本原理均没有发生改变：①借助圆形钢管对核心混凝土的套箍约束作用，使核心混凝土处于三向受压状态，从而使核心混凝土具有更高的抗压强度和压缩变形能力；②借助内填混凝土的支撑作用，增强钢管的几何稳定性。且火灾后外层钢管力学性能有较大恢复，使得钢管仍能有效约束核心RPC，保持了钢管混凝土的套箍约束效应。因此，火灾后钢管和RPC仍有较好的相互作用基础，使得火灾的钢管混凝土柱仍具有较好的抗爆性能。

若定义钢管RPC柱在爆炸荷载作用下的最大位移差值与最大位移之比为其恢复能力系数，图23为钢管RPC柱在比例距离为1 m/kg1/3时的变形恢复系数随受火时间的关系曲线，从图中可以看出，火灾后钢管RPC柱的变形恢复系数随受火时间的增加而减小，受火60 min后的钢管RPC柱仍有60%以上的恢复能力，表明受火后钢管RPC柱仍有较好的恢复能力。

图23 变形恢复系数随受火时间的关系曲线Fig.23 Relation between deformation recovery coefficient and fire time

4 结 论

本文利用ANSYS/LS-DYNA软件对火灾后钢管RPC柱的抗爆性能进行了数值模拟，采用参数化分析方法研究了荷载参数(受火时间、爆炸荷载、轴向荷载)、几何特征参数(钢管壁厚、长径比)和材料性能参数(钢材强度)对火灾后钢管RPC柱动力响应的影响规律，并进一步分析了对其破坏形态的影响，得出以下结论：

(1)火灾后钢管RPC柱在爆炸荷载作用下跨中最大位移随受火时间、轴向荷载、长径比的增加而增大，随比例距离、含钢率、钢材强度的增加而减小。其中，比例距离、受火时间、长径比的影响最为显著，而轴向荷载、含钢率和钢材强度的影响较小。

(2)火灾后钢管RPC柱在爆炸荷载作用下钢管和核心RPC仍能相互作用，保持较好的共同工作，具有良好的变形和耗能能力，表现出良好的抗爆性能，适用于抗火抗爆组合结构。

(3)火灾后钢管RPC柱力学性能劣化，但仍表现出较好的抗剪能力，在爆炸荷载作用下以弯曲破坏为主。随着比例距离的减小和受火时间增加，柱端塑性区扩大，逐渐表现出现弯剪破坏的趋势。