一种单面瓦楞机新型压力辊机构的振动分析

陈志君,杜群贵

(华南理工大学 机械与汽车工程学院,广州 510640)

包装行业中，具有绿色环保、纸材料可回收等优点的瓦楞纸箱得到了大力推广与支持[1]。为了适应市场的需求，瓦楞机不断向着高速化方向发展，而作为核心的压力辊机构，新型机构也不断出现，以适应这一需求。文献[2]研究了一种快速换辊机构，当需要维护、保养时，可以很容易实现压力辊的更换。但早期的压力辊机构是采用气缸、凸轮和限位杆的组合，通过生产人员基于经验调整凸轮与限位杆的接触位置使压力辊保持合理的压力，长期以来效果并不理想，难以满足产品的性能要求，而且调整效率较慢[3]。为了克服以上缺点，出现了皮囊气缸、电动推杆和顶杆的组合结构，通过控制电动推杆可快速实现对压力辊位置的调节，但由于皮囊气缸压力及顶杆刚度不够，造成压力辊的振动过大，电动推杆容易损坏[4]。最近，市场发展出了一种新型的压力辊机构，通过伺服电动缸、偏心轮调节压力辊位置，并在皮囊气缸与液压缸的共同作用下，以减少压力辊的振动。本文将对该新型机构展开振动特性的分析。

瓦楞纸板的黏合强度与压力辊的振动有着密切的关系，若振动幅值过大，会使瓦楞纸板形成高低坑(压痕深一条浅一条的现象)，严重影响了瓦楞纸板的黏合强度。针对瓦楞机的振动问题，众多学者开展了相关研究。文献[5]对瓦楞辊与压力辊的中心距进行了分析，建立了中心距的数学方程，计算了中心距变动的加速度大小。文献[6]研究了单面瓦楞机的共振情况，分析表明当线速度达到180 m/min时，共振非常剧烈，生产出的纸板质量很差。文献[7]将上、下瓦楞辊简化为单自由度振动系统，把上、下瓦楞辊啮合过程中理想中心距的变动量作为位移激励，求得了瓦楞辊的动态响应。文献[8]对旧式的压力辊机构进行了动力学建模，分析了机构产生共振的原因，但并没有对振动响应作出定量的分析。本文对国内某种瓦楞机的新型压力辊机构进行了动力学建模，求得了压力辊的振动响应，通过振动测试进行验证，并和旧式机构进行了对比。最后，对压力辊机构进行改进，进一步减少了压力辊的振动。

1 压力辊机构振动系统建模

图1是目前市场上新出现的一种压力辊机构的工作原理图，通过伺服电动缸、偏心轮组合结构可对压力辊的位置实现快速、精准的调节，液压缸的加压作用则进一步减少了压力辊的振动。压力辊支架是与皮囊气缸、液压缸相连，可绕着固定铰链摆动，以适应工作过程中压力辊与上瓦楞辊周期性变化的中心距，这是造成压力辊振动的主要原因。工作时，原纸经过上、下瓦楞辊的啮合，形成带有瓦楞的芯纸并包裹在上瓦楞辊上，在上浆辊的作用下，使波峰被均匀地涂上胶，最后与面纸在压力辊合适的压力下黏合成单面瓦楞纸板。

1-皮囊气缸;2-导纸辊;3-压力辊;4-压力辊支架;5-偏心轮;6-伺服电动缸;7-液压缸;8-上瓦楞辊;9-上浆辊
图1 压力辊机构工作原理图
Fig.1 The principle graph of pressure roller mechanism

根据图1工作原理图可得到机构的弹簧-质量-阻尼模型，为4个转动自由度，见图2。压力辊通过轴承与压力辊支架相连，通过皮囊气缸1、8(等效刚度为K1，阻尼为C1)的加压，伺服电动缸4、11(等效刚度为K22，阻尼为C22)对偏心轮3、10(偏心轮与压力辊支架的接触刚度等效为K21，阻尼为C21)位置的调节，最后在液压缸5、12(等效刚度为K3，阻尼为C3)的作用下，使压力辊与上瓦楞辊之间保持合理的压力，保证瓦楞纸板的黏合质量。上瓦楞辊为主动辊，图1的局部放大图显示了上瓦楞辊与压力辊的啮合过程，并将上瓦楞辊与压力辊的啮合等效为接触刚度K4。由于不符合渐开线齿廓啮合原理，啮合过程中的中心距是呈周期性变化的，使压力辊产生振动冲击。

1、8-皮囊气缸;2、9-压力辊支架;3、10-偏心轮;4、11-伺服电动缸;5、12-液压缸;6-压力辊;7-压力辊与上瓦楞辊的啮合
图2 压力辊机构弹簧-质量-阻尼模型
Fig.2 The spring mass damping model of pressure roller mechanism

本文只关注压力辊的振动特性，可对压力辊机构进行合理的简化。将伺服电动缸、偏心轮看成一个整体结构，根据系统的能量守恒可得到等效后的刚度为

(1)

伺服电动缸的刚度由内部的滚珠丝杆所提供，阻尼系数C22很小，在此忽略不计，只考虑偏心轮与压力辊支架的接触阻尼C21，因此，简化后的C2=C21。接触阻尼的大小与两接触物体的相对速度和切入的深度有关[9]，为了提高上瓦楞辊和压力辊的抗磨损能力，辊体材料采用具有超高硬度的48CrMo，振动过程中，其切入深度和相对速度都较小，所产生的阻尼力与接触力相比可忽略不计，只需考虑两辊之间的接触刚度所产生的接触力即可。简化后的模型变成了两自由度的振动系统，见图3。

1.1 振动系统数学模型

简化后的压力辊机构的振动系统，一共具有两个自由度，分别为θ1，θ2，根据拉格朗日的理论来建立系统的振动微分方程，考虑到阻尼引起的热能耗散[10]，n自由度系统的拉格朗日方程可写为

(2)

1、6-皮囊气缸;2、7-伺服电动缸与偏心轮等效机构;3、8-液压缸;4-压力辊;5-压力辊与上瓦楞辊的啮合;9、10-压力辊支架
图3 压力辊机构简化模型
Fig.3 The simplified model of pressure roller mechanism

(3)

压力辊的动能和势能

其中，M1为压力辊的质量，J1为压力辊相对于质心的转动惯量。

左端压力辊支架的动能、势能和耗散能

右端压力辊支架的动能、势能和耗散能

其中，J2为压力辊支架相对铰链的转动惯量。

分别把压力辊机构各部分的动能、势能，以及耗散能代入L=T-U和D中，再代入式(2)中，可得到压力辊机构系统标准的振动微分方程

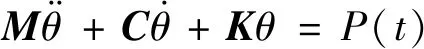
(4)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵，以及P(t)和θ分别为

1.2 系统振动模型求解

(1)液压缸等效刚度K3、等效阻尼C3的确定

刚度K3的大小与液压油的体积弹性模量有关，可根据式K3=GA/L计算得到[12]，其中A为液压缸的工作面积，L为液压缸一端油液的液柱长度，G为液压油的体积弹性模量，在一定范围内会随着工作压力升高而增大[13]。C3为黏性阻尼，严格意义上来说与P、V、T都有关系，但P、V对它影响较小，且实际的动态过程可视为等温过程，可把液压缸的黏性阻尼视为常数，一般通过实验测试得到，根据文献[14]，相同尺寸型号的液压缸阻尼可取C3=1.325 5×104Ns/m。

(2)接触刚度K21、K4，接触阻尼C21确定

根据广义的Hertz接触理论来计算接触刚度[15]和接触阻尼[16]的大小

(5)

(6)

式(5)中：R1和R2分别为两个接触体的曲率半径；E1、μ1和E2、μ2分别是两个接触体的弹性模量、泊松比。式(6)中K为接触刚度，e取值为0.5，为碰撞过程的恢复系数，v0为物体发生碰撞时的初始相对速度，δ为碰撞过程中的两物体相对变形量，m为两接触体的综合质量。对于本研究中接触体材料的参数见表1。

表1 接触物体材料具体参数Tab.1 The specific parameters of contact body

将数据代入式(5)和式(6)中，可求得K4=7.433×109N/m，K21=5.375×1010N/m，C21=4.292×105Ns/m。

压力辊振动的过程中，偏心轮与压力辊支架并不是一直接触的，当伺服电动缸调整好后，在皮囊气缸和液压缸的加压作用下，偏心轮会存在一定的预压缩量，使得压力辊支架向下转动角度θe，当θ>θe时，偏心轮与压力辊支架分离，当θ≤θe时，偏心轮与压力辊支架接触，因此，压力辊机构是含有间隙的碰撞振动系统，具有很强的非线性和不连续性。含有非线性因素的振动系统求解会变得非常的困难，可根据线性平均法[17]对其进行线性化的处理，由于振动角位移引起的非线性因素如下所示

(7)

式(7)中A为压力辊振动角位移幅值，为了便于对K21进行线性化的计算，这里设振动角位移θ=Acos(φ)，φ对应于偏心轮变形得到的角度，与偏心轮的静刚度有关，因此，刚度K21可表示为

(8)

(3)微分方程的求解

压力辊机构的固有频率与阻尼没有关系，只需令P(t)=0，就可以得到压力辊机构系统的自由振动方程

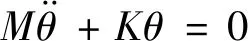
(9)

令行列式|K-ω2M|=0，可求得系统的固有频率

(10)

通过测量与计算，压力辊机构的具体参数见表2。

表2 压力辊机构参数Tab.2 The parameters of pressure roller mechanism

将上述参数代入方程，可以求得固有频率，再代入式(9)，可以计算得到正则振型矩阵

式(4)的振动方程中，存在着惯性耦合和弹性耦合项，不能直接进行求解，可引进正则坐标和正则振型，使方程解耦，令：θ=Ψξ

那正则坐标下的系统振动方程可写成

(11)

其中

由此，可把式(11)写成两个相互独立的单自由度振动方程

(12)

(13)

对式(12)、(13)进行求解，可分别求得自由振动ξ1、强迫振动ξ2，再代入θ=Ψξ，可得到

对于自由振动ξ1，在稳态阶段已衰减为0，因此系统稳态阶段的响应为：θ1=θ2=ξ2，式(13)稳态阶段的响应即为系统的解。

中心距是呈周期性变化的，周期T=2π/w0z，w0为上瓦楞辊的角速度，在一个周期内，中心距的表达式为O1O2=R2cosα1+R2cosα2，其中，R1为上瓦楞辊齿顶圆弧的圆心所在圆的半径，R2为压力辊的半径与上瓦楞辊齿顶圆弧半径之和，由于R1与R2非常接近，因此，α1≈α2=w0t，中心距的表达式可写成

O1O2=(R1+R2)cosα1=(R1+R2)cosω0t

进一步可得到中心距变化量x0的表达式

x0=(R1+R2)-O1O2=

(R1+R2)(1-cosω0t)

(14)

把式(14)代入式(13)中，可以得到

K4L(R1+R2)(1-cosω0t)

(15)

式(15)的右边并非简谐函数的形式，需要对其进行谐波分析，将激振力转为一系列不同频率的简谐函数相加的形式，再使用叠加原理求得系统的稳态响应。

式(15)右边经谐波分析后可得

其中，ω1=2π/T=ω0z，此时令

可以得到系统的稳态响应为

(16)

上式的二阶微分即为稳态响应的加速度

(17)

2 试验与实例分析

2.1 试 验

为了验证所建模型的准确性，有必要对压力辊进行振动测试。瓦楞辊(辊型为C坑，齿数z=194)的线速度为v=180 m/min=3 m/s，R=0.248 75 m，啮合频率为f=vz/2πR=372.4 Hz。瓦楞机工作时，压力辊随着上瓦楞辊转动同时，还绕着压力辊支架摆动中心作上下振动。受到瓦楞机结构和实验设备的限制，难以直接测量压力辊支架的振动角加速度信号。因为压力辊支架变形极小，可看成是刚体，可以在压力辊支架上安装线加速度传感器，测量该点的线加速度信号，如图4所示(l=100 mm，为压力辊支架上传感器安装位置与固定铰链的距离)。根据ε=αl，将理论求解得到的角加速度转化为线加速度，再与测试信号进行对比，以验证模型的准确性。实验中采用的是PCB压电公司生产的NI数据采集器以及与之相配套的加速度传感器。考虑到上瓦楞辊与压力辊的啮合频率，取采样频率为6 400 Hz，当瓦机工作线速度稳定时，采样1 s。

图4 压力辊机构振动测试实验Fig.4 Vibration test on pressure roller mechanism

2.2 数据分析

通过数据采集器采集到的振动信号数据往往叠加了随机噪声信号，还会因为测试仪器温度的变化造成零点漂移而使信号含有不规则的趋势项[18]。本文采用多项式拟合最小二乘法去除信号中的趋势项，再使用五点三次平滑法对信号进行预处理[19]，以消除原始信号中含有的高频随机噪声，提高信号的平滑度，再将理论曲线与实验曲线进行对比，见图5。通过傅利叶变换对两种方法得到的数据进行频谱分析，得到了频谱图，见图6。

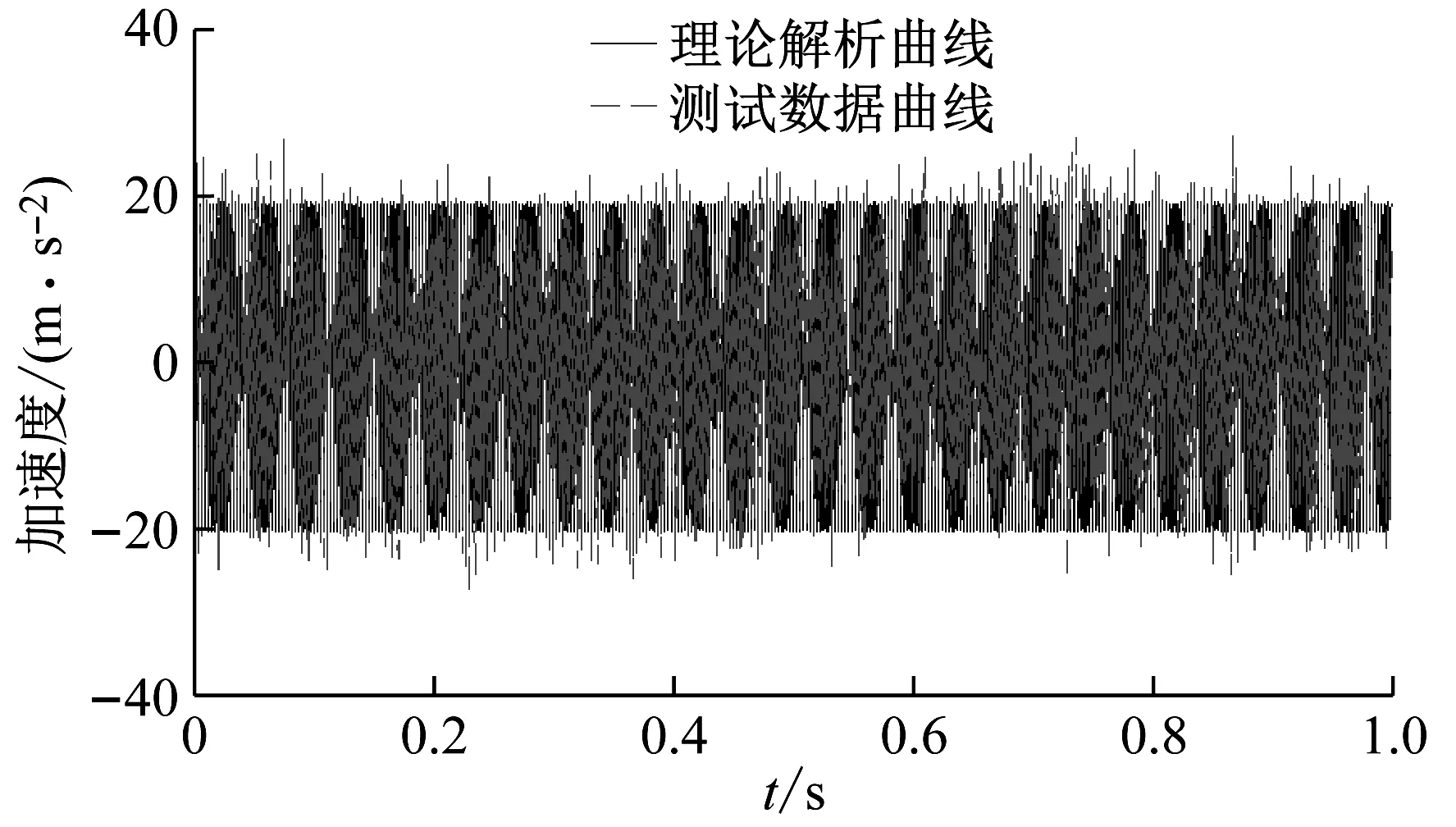
(a)1 s内加速度曲线

(b)0.12 s附近放大图图5 振动加速度时域波形曲线Fig.5 The time domain waveform of vibration acceleration

从图5可以看出，无论是波形还是幅值，实验测试加速度曲线与理论曲线都非常接近。相比理论曲线，实验测试的时域曲线波峰后半侧有较为明显的下降。这主要是因为在建立模型过程中，使用了线性平均法对偏心轮结构与压力辊支架的接触刚度进行了线性化的处理，计算到的刚度值是一个平均值。而在实际结构中，由式(7)可知，当压力辊支架的振动角位移θ>θe，此时偏心轮结构的实际刚度应为零，在外部激励作用下的实际加速度应较小一些。当机构继续向下振动，使得压力辊支架与偏心轮结构接触时，会产生二次冲击，使得实测加速度突然升高，然后再缓慢下降。但总体上，实测加速度曲线与理论曲线基本重合，两者的误差非常小，也由此证明了对模型进行线性化处理的合理性。

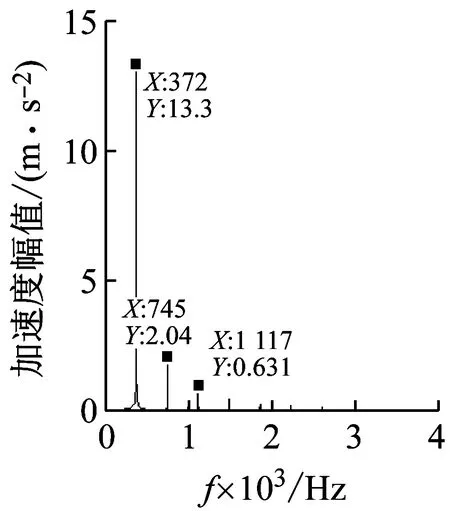
(a)理论加速度频谱

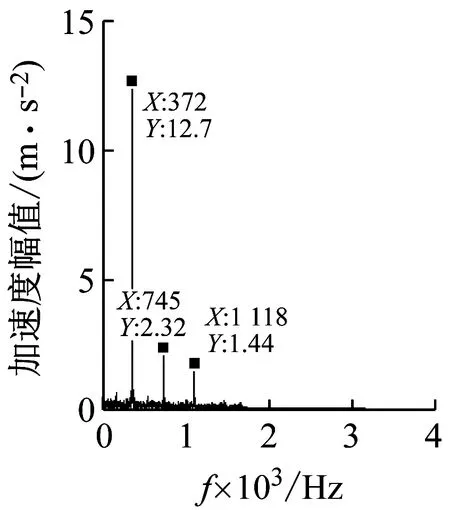
(b)实验加速度频谱图6 加速度频谱Fig.6 Vibration acceleration frequency spectrum

由图6可以发现，两者的特征频率成分几乎是一致的，频域上振动加速度的频率成分主要包含了啮合频率(372 Hz)、两倍频以及三倍频，更高次的倍频成分幅值已接近于零。实验数据的两倍频和三倍频成分幅值有所增大，这主要是因为瓦楞机在工作一段时间后，压力辊的表面和两端的轴承会发生磨损，造成压力辊偏心转动，出现动不平衡，使得倍频成分的幅值比理论频谱有所变大。另外，由于条件的限制，测试现场的噪声非常大，平滑处理只能消除高频成分的随机噪声，对于低频噪声，尚没有很好的算法进行消除。因此，测试信号叠加的低频随机噪声会使实验测得的幅值比理论解析求得的幅值有所变大。

3 分析与优化

瓦楞机实际工作过程中，其线速度并不是固定的，一般可在120～190 m/min进行调节，以适应不同工况的需要。新型压力辊机构的振动情况与激振频率紧密相关的，而激振频率是与瓦楞辊的线速度成正比的。因此，瓦楞机的线速度是影响新型压力辊机构振动的主要因素之一，需要分析压力辊机构在瓦楞机常见的线速度范围内的振动情况。因此，作出了新型压力辊机构中压力辊支架振动角加速度幅值、激振频率随着线速度变化的曲线，见图7。

由图7可以发现，随着瓦楞机线速度的提高，振动会越来越剧烈，当线速度达到165 m/min时，此时的激振频率为341.3 Hz，与机构的二阶固有频率非常接近，造成机构的共振，振动加速度显著增大。因此，在为瓦楞机选择合理的线速度时，应尽量避开压力辊机构共振区所对应的线速度，以避免机构振动过大。

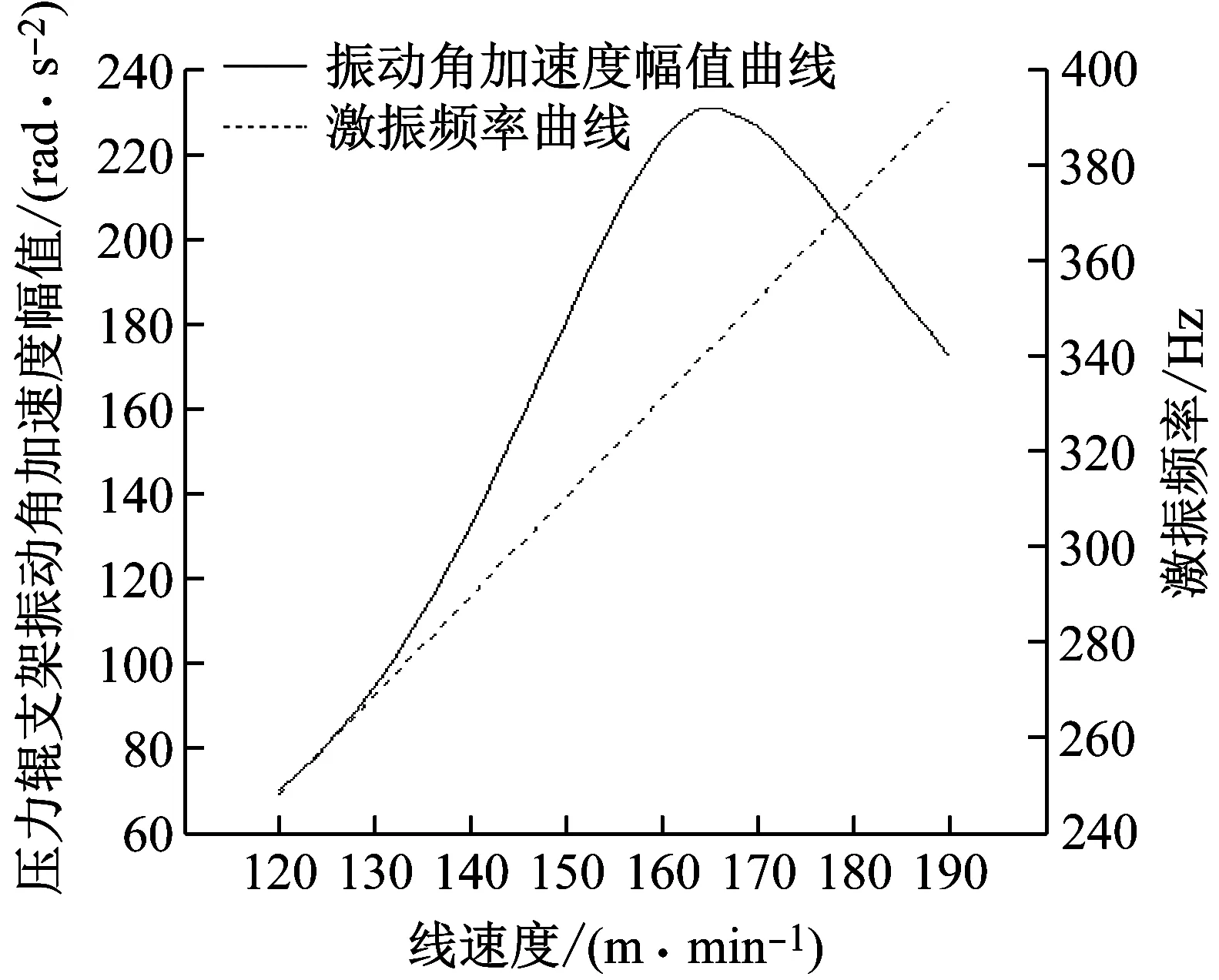
图7 振动角加速度幅值、激振频率随工作线速度的变化Fig.7 The variation amplitude of angular acceleration and excitation frequency with the speed of working line

为了验证新型压力辊机构的减振性能，有必要和旧式压力辊机构的振动特性进行对比。旧式压力辊仅仅由皮囊气缸加压，使用电动推杆、偏心轴调节顶杆的位置来实现对压力辊的调节，其振动方程具有与式(11)相同的形式，将相关参数代入，使用MATLAB作出新旧压力辊随线速度变化的振动幅值曲线，如图8所示。在共振区，旧式压力辊的振动幅值明显较大，严重影响了瓦楞纸板的黏合效果。采用新型压力辊机构，振动幅值由0.024 3 mm下降到了0.014 8 mm。

图8 压力辊振动幅值随工作线速度的变化Fig.8 The variation amplitude of pressure roller with the speed of working line

为了避免压力辊机构在常见的线速度范围内发生共振，更好提升新型机构的性能，本研究对新型压力辊机构进行了进一步的改进。由式(10)可知，压力辊机构的固有频率与刚度K2、K3有关。综合考虑到结构尺寸的限制和成本，增大偏心轮半径到135 mm，增加L22到380 mm，可将刚度K2增大到3.861×109N/m。选用有效直径更大液压缸，增大缸径到120 mm，增大工作压力到10 MPa，可将刚度K3增大到3.25×108N/m。作出了机构进一步改进后的压力辊振动幅值曲线，见图8。

从图8可以发现，瓦楞机线速度在120～190 m/min之间变化时，新型压力辊振动幅值显著减少。并通过进一步的优化，提高了机构的固有频率，使得瓦楞机工作频率带绕开了机构的共振频率，并使振动幅值进一步降低。受到瓦楞辊，压力辊，以及辊两端轴承磨损的影响，为避免出现严重的动不平衡，目前，该型号瓦楞机的线速度一般不会超过200 m/min，该减振方案是可行的。

4 结 论

对单面瓦楞机一种新型的压力辊机构进行了动力学建模，根据广义Hertz接触理论计算模型中的接触刚度和接触阻尼的大小，考虑系统中非线性因素的影响，对模型进行了线性化处理，求解得到了系统的振动响应，并与振动测试得到的加速度信号进行对比，验证了模型的准确性。

最后对比了新旧压力辊机构的振动特性，并对新型压力辊机构进一步优化，通过增大刚度K2、K3提高了机构的固有频率，避开瓦楞机正常工作线速度下的激振频率，避免了共振的发生，进一步减少了压力辊的振动幅值，提高了瓦楞纸板的成型质量。