基于瞬时铣削力系数法的拼接模具铣削稳定性研究

岳彩旭，郝小乐，王彦武，高海宁，马 晶，冯 磊

(1.哈尔滨理工大学 机械动力工程学院，哈尔滨 150080;2.哈尔滨理工大学 先进制造智能化技术教育部重点实验室，哈尔滨 150080)

汽车覆盖件模具加工过程中，由于部分零件表面形状复杂多变，在局部位置上有特殊的硬度要求，致使模具型腔凹凸不平。需要根据零件不同部位受力、受热特征采用不同硬度的模具拼接而成，将不同硬度的镶块分离淬火后再拼接成整体件来保证模具的轮廓精度，并改善模具的加工工艺。由于不同硬度工件拼接的影响致使铣削拼接过缝处时铣削力幅值明显变化并加剧振动，进而降低工件表面质量和刀具的使用寿命，如何在拼接过缝处平稳过渡是亟待解决的问题。为此，本文提出基于瞬时铣削力系数法的铣削稳定性预测模型，来解决铣削拼接模具过程的振动问题，该预测模型可以为大型汽车覆盖件铣削加工提供理论参数依据。

获得铣削力系数是完成铣削稳定性预测研究的基础，针对铣削力系数研究方法国内外学者从多方面进行探究，其中Gonzalo 等[1-2]对铣削力系数随切削参数变化规律深入研究，得到了切削力系数与瞬时切厚、倾角的关系表达式，并结合试验与理论验证该方法的优势。Campatelli等[3]提出了铣削力系数随速度变化的规律，研究结果表明切削力系数在低速区数值偏大，在高速区数值先减小后增大。Grossi等[4]利用传统的平均力法和基于遗传算法的瞬时估计法得到铣削力系数。最后验证表明瞬时估计法更加准确有效。Wang等[5]通过平均铣削力法结合槽切试验得到切削力系数，研究了切削参数对铣削力系数的影响规律，得出在主轴转速(500～1 500 r/min)范围内切削参数不影响切削力系数的结论。岳彩旭等[6]基于动态铣削力系数法结合改进的半离散时域方法仿真得到铣削过程稳定性预测曲线。Gonzalo等[7]提出一种能够预测瞬时铣削力模型，在综合考虑了刀具材料属性、切削参数以及刀具几何等因素，得到的模型较平均法的预测精度高5%。

在研究铣削稳定性时多用稳定性叶瓣图来判断是否发生颤振，稳定性叶瓣图的边界是由临界切削深度和主轴转速关系绘制的预测曲线，颤振预测模型方法主要分为频域法、离散法、数值法等。在利用频域法求解铣削稳定性颤振模型方面诸多学者对此进行了研究，Altintas[8]建立了多自由度动力学模型，提出了零阶求解法，通过求解特征方程根获得无颤振发生下的临界铣削深度，该方法计算效率高，但精度较低。Merdol等[9]在零阶求解法的基础上提出了多频率法，综合考虑了定向因子的高次谐波以及刀具-工件间的传递函数，提高了频域法的计算精度。Bachrathy等[10]将多频率求解法应用到动态特性研究中，不仅考虑了时滞因素影响，而且将二分法与多频率法进行结合，又进一步提高了频率法的计算效率与计算精度。离散法可分为全离散法、半离散法、有限元法等。宋清华等[11]采取半离散方法利用共振区半带宽理论研究了稳定性预测曲线与工件表面质量的关系，通过试验综合验证分析了共振区的稳定性预测曲线的精度。李忠伟等[12]运用Magnus-Gaussjan截断法来获得不同参数条件下的铣削稳定性叶瓣图，在提高了原半离散法的计算精度的基础上，又减少了仿真的计算时间。全离散首先由Ding等[13]提出，运用了数值积分的方法对时滞周期等分离散，再求解振动微分方程的特征值，根据Floquet理论判断是否发生颤振。Liu等[14]综合考虑了复杂曲面特征以及刀具前倾角对瞬时切屑厚度影响等因素，利用全离散法得出了曲面特性对稳定性时域的影响关系。Bayly等[15]分别进行了单、双自由度动力学建模研究，主要对铣刀是否参与切削所导致的动力学变化而进行深入研究。后续Ding等[16-18]通过运用时间有限元方法，将有限元法改进成考虑再生效应等延迟项的半解析方法来预测铣削稳定性，重新建立了随周期系数矩阵变化的积分表达式。Liang等[19]提出了一种改进的数值积分法，基于变化时间延迟，利用偏移矩阵对Floquet过渡矩阵进行修改，得到时滞对稳定性变化影响趋势。

在上述铣削稳定性研究中，多数采用平均铣削力系数法来获取仿真所需的铣削力系数，由于拼接模具铣削过程存在不同硬度拼接及切入冲击，致使铣削力幅值增大，随着加工的进行铣削力幅值逐渐减小，为此拼接模具铣削过程铣削力系数是变化的，而平均铣削力系数不能体现该过程，所以本文采用瞬时铣削力系数法。基于瞬时铣削力系数法所得到的稳定性预测曲线分为上下限两部分，每部分存在多条预测曲线，选择任意一条上下限预测曲线不能准确预测铣削系统是否发生颤振，故本文利用最小包络法来得到极限稳定域，根据上下限选取各个稳定性叶瓣的最低包络点以形成的最小包络叶瓣带作为最终的稳定边界；最后通过时频域分析综合验证模型的准确性，其结果可以为大型汽车覆盖件铣削加工过程提供理论参数依据。

1 拼接过缝处切厚模型

在动态铣削过程中，当刀具与工件接触而产生振动，每一刀齿都会留下振纹，当下一刀齿切入时会再次产生波动。铣削振动影响瞬时变化的铣削厚度，而且前一刀齿波动也会影响。建立拼接模具铣削过程的瞬时切厚模型需要先划分铣削区域，根据单硬度区域、多硬度区域来分段式求解瞬时切削厚度。

1.1 铣削区域的划分

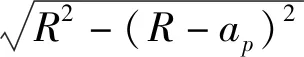
(1)

由式(1)可知，当0≤t≤td时，在同时铣削相邻两个不同硬度工件时，铣削过程由60HRC工件切向50HRC工件，取铣刀螺旋刃上的一点P，切削区域的划分示意图如图1所示。

可以根据P点的位置来判断铣削厚度，可以分成两种情况：第一种为P点处在铣削高硬度60HRC区域(第一硬度区域)；第二种为P点处在铣削低硬度50HRC区域(第二硬度区域)。设定沿进给方向上P点距切削圆中心轴线的距离表示为Rp=Rsinθjisinκ。以此可以得到当前刀齿的P点距拼接缝的距离dj，表示为

(2)

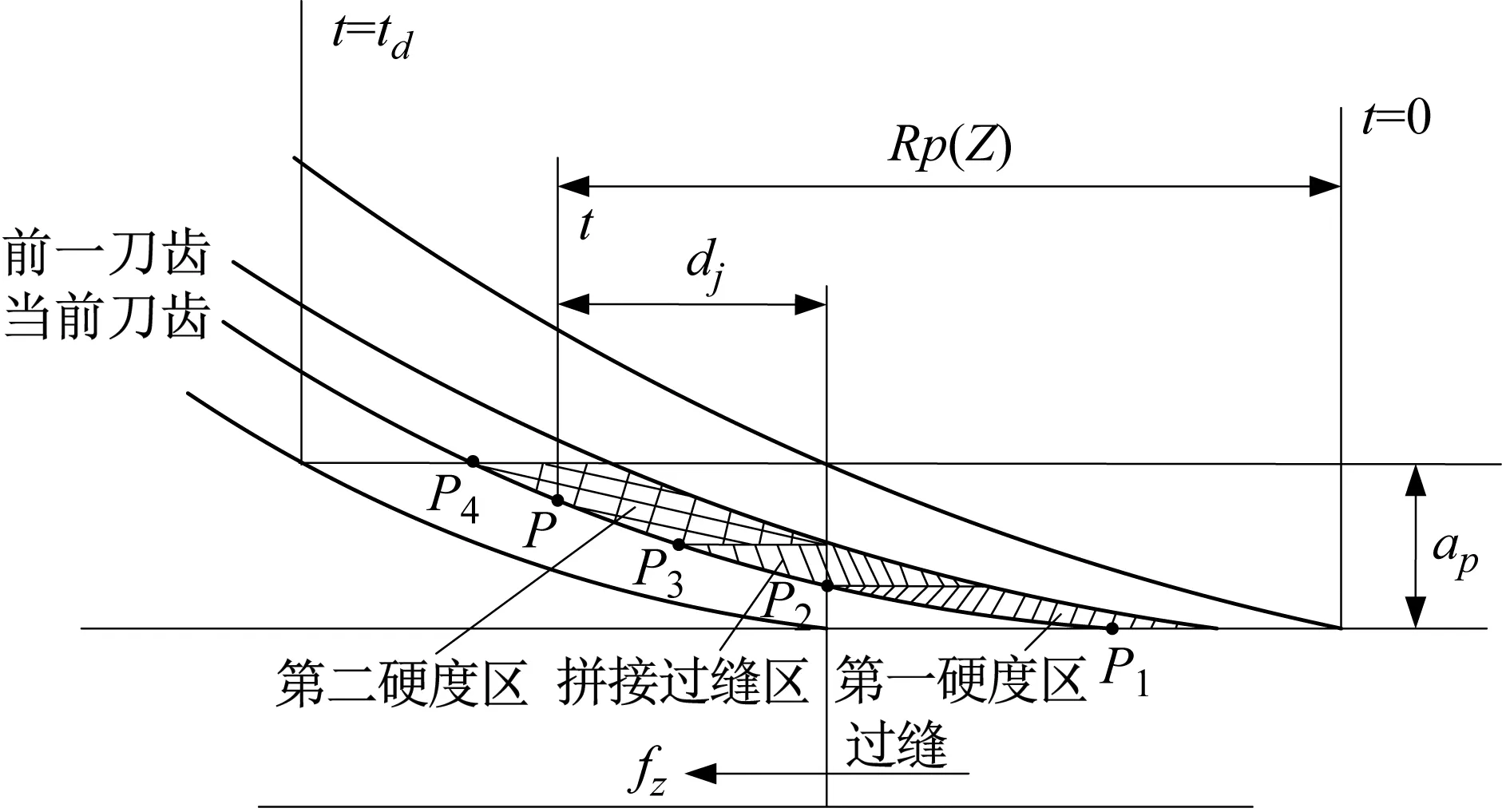
图1 切削区域的划分示意图Fig.1 Division of cutting areas

当dj≥0时，则P点处在铣削单一硬度(低硬度)50HRC区域。否则，P点处在单一硬度(高硬度)60HRC区域。

1.2 拼接过缝处的切削厚度

切削厚度可以表示为hs，前一刀齿轨迹距拼接处的距离dj-1表达式为

dj-1=dj-hssinκ

(3)

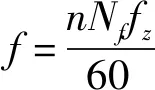
hs=fzsinθjisinκ

(4)

当dj-1<0时，同时铣削两种硬度工件，此时切削厚度需要分两段来计算，hs1和hs2分别表示P点在过缝前后的切削厚度，如图2所示。

(a)切厚三维示意图

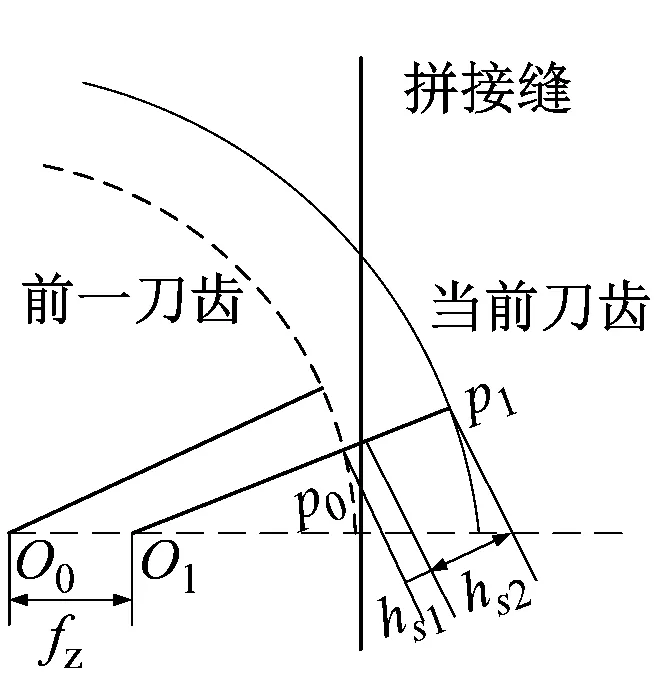
(b)切厚平面示意图图2 切厚三维示意图Fig.2 Three-dimensional sketch of cut thickness

图2中|PP1|即为切屑厚度。

根据上述静态厚度表示为hs，当前刀齿轨迹P点距拼接处的距离为dj，可以得到

(5)

则该点的三个方向铣削力公式根据切厚的表达式不同需要分段来计算，拼接区域的切向、径向和轴向的铣削力表达式，将上述公式转化为X、Y、Z三个方向铣削力公式为

(6)

当dj≤0时，则P点处在铣削单一硬度(低硬度)60HRC区域。则该点的铣削力在X、Y、Z方向的表达式为

(7)

式中：N为齿数；φ1、φ2分别为第j齿参与切削时最小、最大位置角。

确定φ1、φ2、φ3、φ4的值，首先要明确P点与刀具几何轴线的距离，点P1，P2，P3和P4分别处在切削刃上三个不同区域的交界处。P1和P4位置角度可以表示为

(8)

在P2处，点P2到拼接缝的距离为零，即dj=0，可以根据式(9)确定φ2。

(9)

在点P3处，前一刀齿轨迹距拼接过缝处的距离为0，则可以根据公式(10)确定φ3。

(10)

上述公式推导出拼接区域的静态切厚，动态铣削过程需考虑再生效应，前后两刀齿由于相位差引起的动态切厚hd表达式为

hd=(vj-vj-1)sinκ

(11)

式中：vj和vj-1分别表示前后两刀齿留下的振动位移，然而，在大振幅的情况下，第(j+1)刀齿不与已加工表面接触，而vj可能是第(j+2)刀齿留下的振动位移，甚至第(j+3)、第(j+4)刀齿。这是由动态铣削过程的非线性导致的，因此vj可表示为

vj=min {vj+1(t-T),vj+2(t-2T)+h,vj+3(t-T)+2h,…}

(12)

t为当前时间，T为连续刀齿运动周期，因为切屑厚度在径向进行测量的，vj转变为X、Y方向为

vj=Δxsinθji+Δycosθji=

[x(t)-x(t-T)]sinθji+[y(t)-

y(t-T)]cosθji

(13)

其中Δx=x(t)-x(t-T)，Δy=y(t)-y(t-T)分别表示为X、Y方向前、后刀齿所产生的动态位移。时滞周期T表达式为T=60/(Nt·n)。

由静态切厚、动态切厚共同构成未变形瞬时切屑厚度h，可表示为

h=(hs+vj-vj-1)g(θj)

(14)

其中g(θj)为判断刀具是否参与切削的函数。刀齿j的铣削力是关于铣削力系数、铣削深度和切屑厚度的函数关系式，公式为

(15)

2 铣削过程的瞬时铣削力系数法的求解

准确获得铣削力系数是得到铣削稳定性预测仿真模型的关键。铣削力系数求解研究方法大体分为两种：① 基于直角切削数据库通过参数转换来获取斜角铣削力系数方法；② 利用快速标定的方法来获取斜角铣削力系数方法。第二种求解铣削力系数的方法又可分为平均铣削力系数法和瞬时铣削力系数法两种。本文所采用的是瞬时铣削力系数法，该方法是在时域部分用最小二乘法拟合仿真结果和试验结果，通过反演的方法来获取铣削力系数。

瞬时铣削力系数求解法利用非线性最优化方法解决最小二乘曲线拟合的问题，并考虑到目标函数定义的上限和下限变量，优化过程使用最小二乘算法，时域仿真的铣削力等同于在每个时间步内测量的铣削力。

在每一个小的时间步dt时域仿真计算铣削力，dt的求解公式为

(16)

式中：fs是铣削力测量过程的采样频率。在每一个时间周期计算瞬时切屑厚度和切削力，刀齿旋转角度为φ，dφ由时间步数和主轴转速决定。瞬时切屑厚度由刀具圆弧路径近似而成，并假设刀具和工件是刚性的。铣削力可以分为切向力Ft、法向力Fn和轴向力Fa，为了得到仿真结果，需将三个方向铣削力进行坐标系转换，表示为

(17)

ds为每一离散单元的切削刃长度，h是未变形切屑厚度，db是每一离散单元的切屑宽度。瞬时铣削力系数是根据仿真铣削力和测量铣削力来计算的，公式可表示为

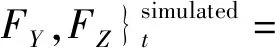
[A(t,θ,κr,h,S)]{Ktc,Kte,Krc,Kre,Kac,Kae}

(18)

把仿真铣削力和试验测量铣削力在t时等同化，方程转变成

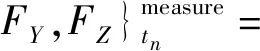
[A(t,θ,κr,h,S)tn]{Ktc,Kte,Krc,Kre,Kac,Kae}

(19)

其中Φ是刀具瞬时旋转角，目标函数被定义为

(20)

其中k是决策变量的向量，包括6个具体的铣削力系数，目标函数在每一时间步仿真力和测量力是不同的。

因为每个模拟瞬时铣削力的时间步长必须和测量时的铣削力是一致的，所得到的方程组取决于采样频率(即时间步数)，求解公式表示为

fn(k)2)

(21)

n是时间步数，曲线拟合问题通过反射算法来解决，常用于求解决策变量的上限或下限。测得的平均铣削力分别用于包括一些相关工艺参数的非线性优化函数，其中参数包括刀具的齿数、铣削力的测量采样频率和决策变量。此处求得不同硬度下铣削力系数将为后期稳定性预测曲线的编程提供参数基础。

3 拼接模具铣削过程稳定性研究及算法分析

根据球头铣削加工特点建立了铣削过程的动力学模型，求解动力学方程时使用Li等[20]提出的基于四阶Runge-Kutta法的全离散法(RKCDM)，此方法是在全离散法的基础上，运用龙格库塔迭代法离散时滞微分方程，简化离散迭代公式的复杂性，提高了仿真的计算效率与计算精度，表现出较好的收敛性。

对于球头刀铣削加工而言，通常都沿X、Y平面进给，刀具受力主要为切向力和径向力，轴向力一般忽略不计，因而建立两自由度的铣削动力学模型。建立拼接模具铣削过程动力学模型时同时考虑了铣削单硬度区域的铣削力与拼接处切入切出的冲击力，以球头铣刀和工件作为研究对象，将刀-工接触模型转化为两个垂直的弹簧阻尼等效模型，在主轴与刀具之间可以把在X和Y方向的微分方程描述为

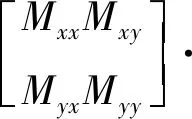
(22)

式中:Mxx、Myy为在X和Y两方向的模态质量；Cxx、Cyy为在X和Y两方向的模态阻尼；Kxx、Kyy为两方向的模态刚度；忽略铣刀X和Y向的结构模态耦合效应，即假设式中Mxy、Myx、Cyx、Cxy、Kxy、Kyx均为0；总切削力分成单一硬度区的铣削力F(t)和拼接处的冲击力F(t)impact两部分。

将上述铣削动力学公式转化为考虑时滞性的二维铣削时滞微分方程为

(23)

式中：ωnx、ζx、kx、ωny、ζy、ky分别表示为X、Y方向上的固有频率、阻尼比、刚度系数；ap是轴向切削厚度；Kt是切向的切削力系数；T是刀齿通过周期；x(t-T)和y(t-T)是时滞项。

g(φj(t))=(2πΩ/60)t+2π(j-1)/N

(24)

式中：Ω是主轴转速，单位为r/min；g(φj(t))为判断刀齿j是否参与切削的函数，被定义为

(25)

式中，φst和φex分别表示刀齿j的切入角、切出角。逆铣时，φst=0且φex=arccos(1-2a/D)；顺铣时，φst=arccos(2ae/D-1)且φex=π，ae/D表示径向浸入率(ae是径向切削深度，D是球头铣刀的直径)。

将式(17)转换到空间形式为

(26)

其中A(t)和B(t)表示时间周期系数矩阵，则A(t)=A(t+T)，B(t)=B(t+T)，T是时间周期，其数值与时滞量相等。τ是时滞时间，在T=τ时为单延迟铣削过程。为了解决A(t)和B(t)，本节使用四阶龙格库塔方法，时间周期T等距离散成m个时间段(m为整数)，每段时间周期为Δt，T=mΔt，m为单齿通过周期的离散数，由经典Runge-Kutta表示成

(27)

式中，ui表示u(i·Δt)，ui+1表示u[(i+1)·Δt]，ti表示idt，变量i为整数且满足0≤i≤m。使用龙格库塔方法，公式依次推导得

(28)

ut+1=Fi·ui+Fi-m·ui-m+Fi-m+1·ui-m+1

(29)

其中系数Fi，Fi-m，Fi-m+1表示为

(30)

其中I是n×n单位矩阵，n是矢量ut的维数。

为了获得传递矩阵，n×(m+1)维度矢量公式为

zi=col(ui,ui-1,…,ui-m+1,ui-m)

(31)

由上式能得到传递方程表达式为

zi+1=Dizi

(32)

因此系数矩阵Di作为一个Di(2m+4)维度矩阵，当i=0,1,…,k-1，(2m+4)维传递矩阵φ表示为

φ=Dk-1·Dk-2…D2·D1

(33)

根据Floquet理论，如果传递矩阵φ的特征方程根有一个大于1，则系统是不稳定的，否则系统是稳定的。因此边界曲线在稳定性图表中被分为稳定区域和不稳定区域，能作为判定是否发生颤振的依据。

4 铣削试验及结果分析

4.1 铣削力系数试验

在拼接区域同一刀齿同时切削两种不同硬度材料，为获得表示该过程切削力系数，基于每一刀齿切削力数据，采用最小二乘曲线拟合法得到瞬时铣削力系数。

试验所需装置包括：奇士乐旋转测力仪，数据采集箱，奇士乐5070A电荷放大器；试验所需工件：硬度为50HRC、60HRC拼接工件。试验所需的刀具为：直径φ=20 mm的刀片式球头铣刀；所需的机床是大连机床VDL-1000E立式四轴加工中心。由于铣削平面工件时球头铣刀刀尖的切削速度为0，所以进行铣削力系数试验时，将工件倾斜放置，倾斜角为：20.4°，如图3(a)、(b)分别为铣削力系数辨识试验所用的数据采集仪、电荷放大器和旋转测力仪。铣削力系数试验机床与工件摆放位置图如图4。

(a)数据采集仪与电荷放大器

(b)旋转测力仪图3 铣削力系数辨识试验所用的仪器Fig.3 Machines and equipment of milling experiment

图4 铣削试验机床与工件摆放布局Fig.4 Milling test machine and workpiece placement layout

此节求得不同硬度下铣削力系数将为后续稳定性预测曲线的编程提供参数基础。

得到拼接区域瞬时铣削力系数的平均值如表1所示，不同切削参数对铣削力系数的影响规律见4.2节。

表1 拼接区域瞬时铣削力系数Tab.1 Instantaneous milling force coefficient of splicing area

4.2 切削参数对瞬时铣削力系数的影响

4.2.1 主轴转速的影响

本节主要针对主轴转速因素进行了一系列铣削试验，并使用瞬时铣削力法求解铣削力系数，保持每齿进给量0.08 mm/tooth、铣削深度0.2 mm保持不变，并选取的主轴转速范围为2 500～6 000 r/min，每次增加的步长为500 r/min。

图5中的三条折线为利用平均铣削力系数法得到的铣削力系数随主轴转速的变化趋势，并利用瞬时铣削力法得到每个主轴转速下铣削力系数的最大值、最小值。图中铣削力系数有一个显著的下降趋势直到临界主轴转速达到4 500 r/min，当超过临界转速4 500 r/min时，铣削力系数有明显上升的趋势，然后平稳。铣削力系数出现下降的趋势归因于高速铣削条件下刀具与切屑相互作用导致温度上升进而导致工件材料出现热软化的现象。

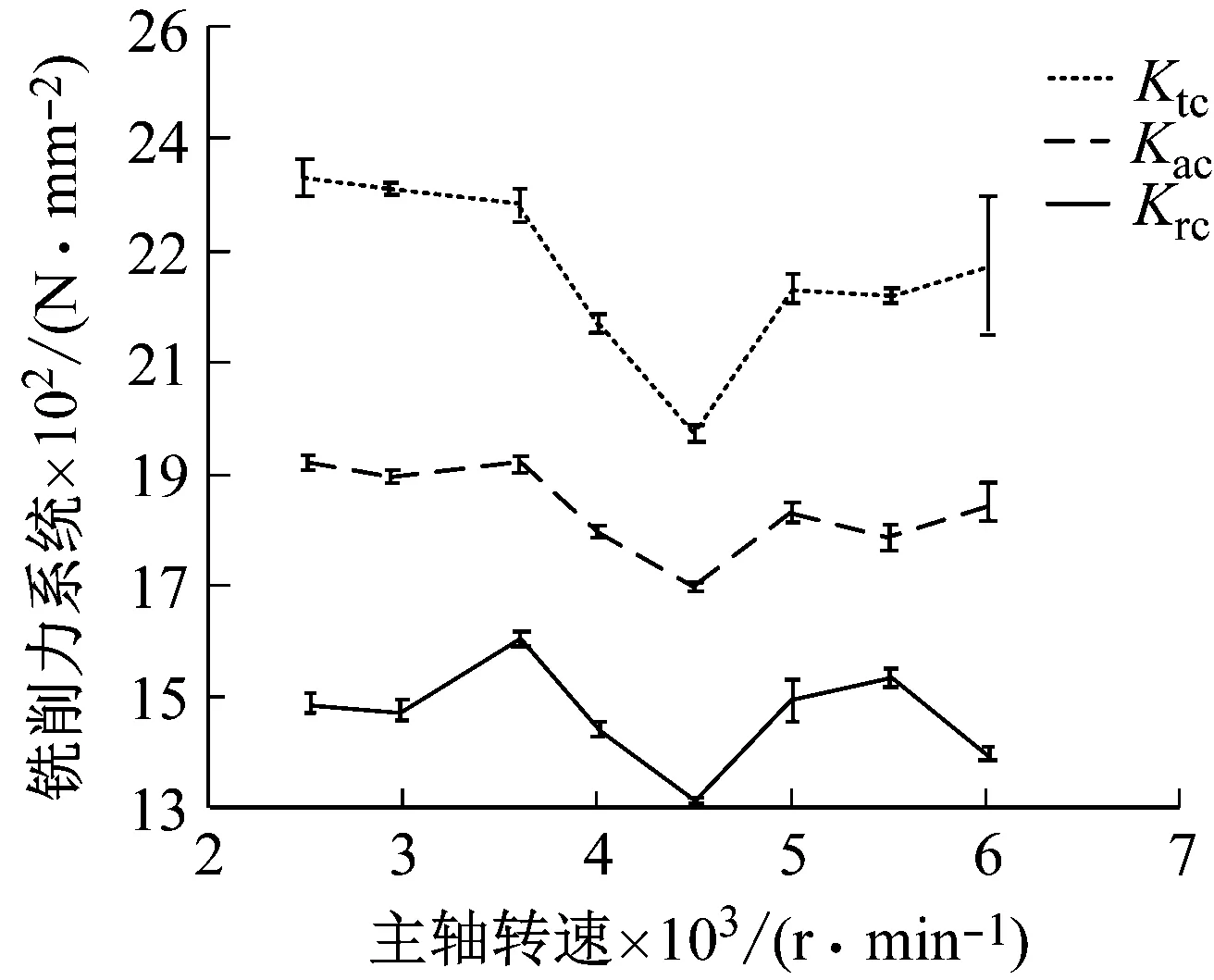
图5 主轴转速对铣削力系数的影响Fig.5 Effect of spindle speed on milling force coefficient

4.2.2 每齿进给量的影响

本节主要针对每齿进给量因素进行了一系列铣削试验，并结合使用平均铣削力系数法以及瞬时铣削力法求解铣削力系数，保持主轴转速4 000 r/min、铣削深度0.2 mm不变，并选取的每齿进给量的范围为：0.05～0.25 mm/tooth，每次增加的步长为0.05 mm/tooth。

图6是在逆铣条件下得到的铣削力随每齿进给量变化的趋势示意图，其中的三条折线为利用平均铣削力系数法得到的铣削力系数随每齿进给量的变化趋势，并利用瞬时铣削力系数法得到每齿进给量下铣削力系数的最大值和最小值。从图中可以发现切向铣削力系数和法向切削力系数随着每齿进给量的改变呈现无规则降低的趋势。然而径向铣削力系数没有显著变化。同一参数条件下进行顺铣试验，发现不同铣削方向的铣削力系数变化趋势是相一致的。

图6 每齿进给量对铣削力系数的影响Fig.6 Effect of feed per tooth on milling force coefficient

4.2.3 铣削深度的影响

由于球头铣刀每一刀齿参与切削区域的不断变化导致瞬时未变形切屑厚度受每齿进给量和铣削深度的影响。当每齿进给量保持固定，铣削深度减小，则瞬时未变形切屑厚度也减小，为了研究径向铣削深度对特定铣削力系数影响，铣削深度设定为0.2～1 mm，每次增加的步长为0.2 mm。保持主轴转速4 000 r/min、每齿进给量0.08 mm/tooth不变情况下来进行一系列铣削试验，使用平均铣削力系数线性法和瞬时铣削力非线性法得到的瞬时铣削力系数结果如图7所示。

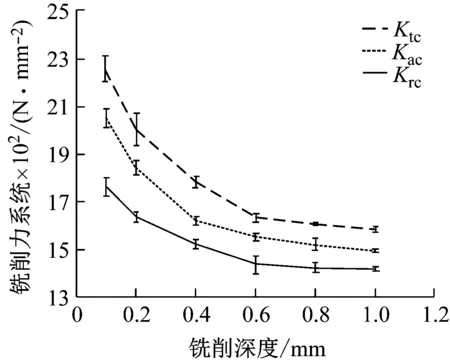
图7 铣削深度对铣削力系数的影响Fig.7 Effect of milling depth on milling force coefficient

从图7可以发现，切向、法向和径向铣削力系数随着铣削深度的改变而显著变化，即呈现不规则减小的趋势，当铣削深度在0.1～0.6 mm之间铣削力系数随着铣削深度逐渐减小，当超过0.6 mm铣削深度时铣削力系数基本保持不变。

4.3 拼接模具铣削稳定性分析

根据上述提出的稳定性预测分析方法，首先输入铣削系统的X、Y和Z方向模态参数，并基于Runge-Kutta法的全离散法进行MATLAB仿真来获得多硬度拼接模具铣削过程稳定性预测曲线。选取一阶模态参数为ωnx=785 Hz，ωny=800 Hz，ωnz=753 Hz，ζx=0.024 6，ζy=0.026 3，ζz=0.021 5，kx=1.74×107N/m，ky=1.71×107N/m，kz=1.21×107N/m，计算步数选取m=40。由于瞬时铣削力系数随着铣削参数的变化而变化，导致不同主轴转速和切深下存在多条预测曲线，选择任意一条上下限预测曲线不能准确预测铣削系统是否发生颤振，故本文利用最小包络法来得到极限稳定域，根据上下限选取各个稳定性叶瓣的最低包络点以形成的最小包络叶瓣带作为最终的稳定边界。最小包罗法适用于任何硬度的拼接件，在获得准确切削系数的前提下，借助于求解动力学的时频域方法，获得相应系数下的叶瓣图，最后用最小包罗法得到稳定性叶瓣带。利用最小包络法得到稳定性预测曲线的步骤为：首先保持每齿进给量0.08 mm/tooth、铣削宽度0.15 mm、刀具参数不变的前提下选取四组切削参数：① 主轴转速3 500 r/min、铣削深度0.15 mm；② 主轴转速3 500 r/min、铣削深度0.2 mm；③ 主轴转速4 000 r/min、铣削深度0.15 mm；④ 主轴转速4 000 r/min、铣削深度0.2 mm，然后求解各组参数条件下的瞬时铣削力系数，得到每个参数条件下的瞬时铣削力系数的上下限，最终分别仿真上限和下限的稳定性预测曲线，通过MATLAB仿真可得到多硬度拼接模具铣削过程稳定性预测曲线如图8所示。

图8 铣削稳定性叶瓣图Fig.8 The milling stability lobes

图8中上部四条曲线、下部四条曲线分别为利用四组切削参数求解的瞬时铣削力系数绘制的上、下限稳定性叶瓣，上、下方粗曲线是利用最小包络法得到的稳定性预测曲线，两粗曲线中间区域为临界稳定区域，即区域内不是所有点都是稳定或不稳定的点，上方为不稳定区域，下方为稳定区域。

4.4 铣削稳定性预测结果的试验验证

根据利用最小包络法得到稳定性叶瓣曲线，选取局部点进行铣削颤振试验，主轴转速选取的范围为2 000～8 000 r/min，每次增加的步长为1 000 r/min，铣削深度选取的范围为0.1～0.6 mm，每次增加的步长为0.05 mm。选用铣削试验机床是大连机床VDL-1000E立式四轴加工中心进行，试验所用的信号采集系统采用的东华DH5922，采用的测力仪为Kistler旋转测力仪，铣削颤振试验的仪器与铣削力系数试验仪器相同。试验所用的刀具为φ=20 mm刀片式球头铣刀，齿数为2，刀具装夹悬伸长度220 mm，工件采用硬度为60HRC、45HRC拼接而成的淬硬钢Cr12MoV。

图9为多硬度拼接淬硬钢铣削稳定性预测曲线的示意图，在图中选取四个参数点进行试验验证，选取四点的切削参数分别为A(n=4 000 r/min，ap=0.1)、B(n=4 000 r/min，ap=0.3 mm)、C(n=5 500 r/min，ap=0.3 mm)、D(n=4 000 r/min，ap=0.6 m)，利用时域振动加速度以及傅里叶变换后的频谱分析综合验证绘制稳定性预测曲线的准确性。

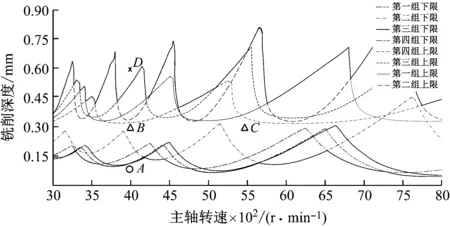
图9 多硬度拼接淬硬钢铣削稳定性预测曲线图Fig.9 Prediction curve of milling stability of multi-hardness splicing hardened steel

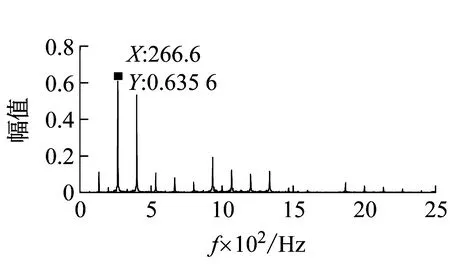
图10(a)、(c)、(e)、(g)分别为A、B、C参数点的振动加速度信号，图10(b)、(d)、(f)、(h)分别为A、B、C点的傅里叶变换频谱图，从图10(a)、(b)可以清晰看出A点的振动加速度波动平稳，幅值为6 m/s2，在傅里叶变换后频谱分析的最大幅值对应的频率为266.66 Hz是刀齿通过频率(4 000×2/60=133.33 Hz)的倍频，综上分析可以判断A点为稳定切削参数。从图10(c)、(d)可以看出B点的幅值有短暂的波动，波动幅度不大，幅值基本维持在9.5 m/s2，较A点高出3.5 m/s2，但从频谱图中最大幅值对应的频率为266.66 Hz可以看出，该频率是刀齿通过频率的倍频，不是颤振频率，综合分析判断B点是稳定切削参数；B、C两点是同一切深不同转速条件下两点，图10(e)、(f)中可以看出C点的振动加速度幅值突变较B点明显，波动的最大加速度幅值达到19 m/s2，且频谱图中最高幅值所对应的频率既不是刀齿通过频率也不是其倍频，该频率为颤振频率，综上分析C点为不稳定切削参数；由于B、C两点处于同一区域，但是通过分析得到该两点一个是稳定切削条件，另一个为不稳定切削条件，故可以得出预测曲线上下限之间区域是临界稳定区域。从图10(g)、(h)中可以看出D点的振动加速度幅值突变明显，且幅值较大，波动的最大加速度幅值达到21 m/s2，最终幅值稳定在15 m/s2，且频谱图中最高幅值所对应的频率2 000 HZ既不是刀齿通过频率也不是其倍频，该频率为颤振频率；综上分析D点为不稳定切削参数。通过对A、B、C、D四点的时域、频域分析，可以得出本文所建立的稳定性预测曲线是准确的。

(a)A点的振动加速度信号图

(b)A点的傅里叶变化频谱图

(c)B点的振动加速度信号图

(d)B点的傅里叶变化频谱图

(e)C点的振动加速度信号图

(f)C点的傅里叶变化频谱图

(g)D点的振动加速度信号图

(h)D点的傅里叶变化频谱图图10 A、B、C、D四点铣削试验验证图Fig.10 Milling test verification diagram at A,B,C,D four points

5 结 论

在拼接模具铣削过程中，针对拼接过缝区域振动突变问题，本文分别建立拼接过缝处的瞬时切削厚度模型、基于瞬时铣削力系数法的铣削稳定性预测模型来深入研究拼接模具铣削过程振动特性，仿真时使用基于Runge-Kutta法的全离散法来实现稳定性预测，该方法计算速度快、精度高，并通过铣削颤振试验来验证稳定性预测曲线的准确性，综上得到以下结论：

(1)从切削参数对瞬时铣削力系数影响研究可以得出：随着每齿进给量与铣削深度的增加，瞬时铣削力系数的上下限都逐渐降低；但随主轴转速的提升，瞬时铣削力系数的上下限呈现先下降后上升最后平稳的趋势。

(2)运用基于瞬时铣削力系数法得到多条铣削稳定性预测曲线，并利用最小包络法得到两条预测曲线的上下限，两条预测曲线中间区域为临界稳定区域，上方为不稳定区域，下方为稳定区域。