状态变换卡尔曼滤波的进一步解释及应用

王茂松，吴文启，何晓峰，潘献飞

（国防科技大学智能科学学院，长沙 410073）

如果捷联惯性组合导航系统建模合理，并且传感器均能良好工作的情况下，大部分基于扩展卡尔曼滤波甚至其它非线性滤波的组合导航系统[1-3]均能较好的工作。但是，当导航平台处于不利的环境下时，如在准静态的环境下，即处于静态的载体仍然受到振动、风动等外部力的影响，一贯的捷联惯性组合导航滤波方式很容易出现方差估计不一致的问题。例如，虽然在准静态环境下，东方向陀螺和水平方向加表是不可观测的，即它们的方差在理论上应该是保持不变的，但是由于振动的存在，会使组合导航系统中它们的方差仍然会继续减少，导致方差的理论值与实际估计值不符，进而导致导航精度的下降甚至是滤波的发散[4]。

为了解决方差估计不一致的问题，学者们提出了一些方法论，如施密特卡尔曼滤波器[5]（Schmidt- Kalman Filter,SKF），将不可观的状态零化，也就是不可观状态对应的方差不进行更新。施密特卡尔曼滤波器实际上为次优滤波器，但是，它可以保证不可观状态估计的一致性，避免估计发散，并成功的应用于目标追踪[6]以及太空探测[7]。Huang 等人[8]指出，在EKF-SLAM 系统中，如果过程模型和量测模型的雅克比矩阵以最近的状态估计进行线性化，将会导致可观测子空间的维度比实际的维度要高，进而使得状态空间中本来不可观测的状态进行错误的校正，产生不一致的问题。所以，作者提出了选择合适的线性化点来使系统的可观测性与实际相符的卡尔曼滤波方式，称为观测约束扩展卡尔曼滤波（Observability Constraint Extended Kalman Filter,OCEKF），通过实验验证了所提出滤波方法的一致性。不变卡尔曼滤波（Invariant Extended Kalman Filter,IEKF）[9]是国外学者最新提出的可以应用于组合导航系统中的滤波方法，核心内容是基于李群李代数的理论，可以防止组合导航系统出现方差估计不一致的问题，在同时定位与构图领域亦得到应用[10-11]。

文献[12]指出导致捷联惯性组合导航系统方差估计不一致问题的主要原因在于系统矩阵中的比力项，通过速度误差状态的严格变换，可以避免系统矩阵中含有比力项，进而克服方差估计不一致的问题。实际上，速度误差的状态变换在本质上与速度误差状态定义的坐标系一致性有异曲同工之妙[13-15]。本文对文献[12]中提出的速度误差从坐标系一致的角度作进一步的解释，并将其成果进一步扩展应用于捷联惯性导航的初始对准和惯性/卫星松组合导航。

1 NED 坐标系基于ST-EKF 的惯性/卫星松组合系统方程

当地导航系下定义的速度微分方程为：

其中，fb为比力向量，gn当地重力矢量，为地球相对惯性系的角速率在导航系的投影，为北东地(NED)坐标系相对地球运动产生的角速率在导航系的投影，∧代表将向量转化为斜对称矩阵，Cbn为姿态矩阵。

其中，φn和分别为姿态误差和速度误差向量，和的定义见文献[12]，δfb为加速度计误差向量。

新定义的速度误差的微分方程的详细推导如下：

其中，εb和∇b分别为陀螺和加速度计的零偏；wg和wa分别为陀螺和加速度计误差的白噪声向量；是姿态误差的微分：

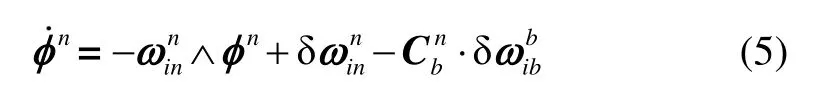
陀螺仪和加速度计误差可以建模为随机游走过程：

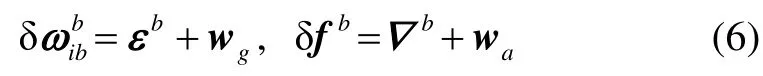
根据雅克比恒等式可以得到：

显然，从式(9)可以看出，新的速度误差微分方程中不再含有比力项，而是由重力向量替代。由于IMU 在一般情况下的输出都是比力增量而不是比力本身[13]，并且比力增量的值由于器件等原因会掺杂着量化噪声，所以传统基于EKF 的组合导航系统的系统矩阵的计算会被动态环境下的比力fn严重影响，进而导致方差不一致性。但是，新的系统矩阵中不再有比力项fn，而是被重力项gn所替代。新的基于状态变换的卡尔曼滤波方式可以避免由于比力量化噪声较大带来的系统矩阵计算不精确的问题，因为对一般载体的当地局部导航来说，gn的变化很小，几乎为常值。

根据新定义的速度误差向量，可以推出位置误差微分方程为：

其中，

根据式(5)(6)(9)(10)可以推导出基于ST-EKF 的组合导航系统在NED 坐标系下的惯导误差状态方程为：

其中，系统矩阵为F，惯导误差状态向量为x，噪声转移矩阵为G，过程噪声向量为w，其对应的协方差矩阵为Q。它们的定义如下：

2 NED 坐标系基于ST-EKF 的惯性/卫星松组合观测方程

基于ST-EKF 的惯性/卫星松组合观测模型可以设计为δz=H x+υ，其中：

式(23)中的H矩阵是根据式(24)得到。

其中，δzv和δzr分别为惯导与卫星之间的速度误差和位置误差，υv,3×1和υr,3×1为对应的观测白噪声。由于卡尔曼滤波估计的是新的速度误差状态，所以，滤波之后速度状态的更新应该根据式(25)进行：

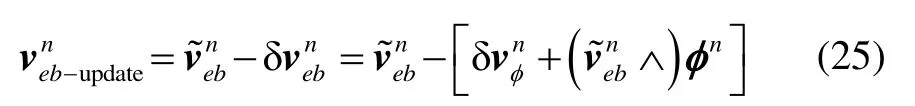
姿态和位置的校正则与传统的EKF 相同[13]。

3 实验结果与分析

3.1 单位置对准实验

本节通过基座振动环境的单位置精对准实验来验证所提出的状态变换卡尔曼滤波的有效性。惯性测量单元为激光陀螺IMU，性能指标参数如表1所示。

表1 激光陀螺IMU 性能指标参数 Tab.1 Specifications of the RLG IMU

捷联惯导系统放置在测试台上静态测试，时间为3600 s，惯性测量单元采样率为200 Hz。为了验证扩展卡尔曼滤波EKF 和状态变换卡尔曼滤波ST-EKF在15 状态情况下即状态不完全可观时的基座振动环境下的对准结果，对原始的比力测量数据加1 mm/s,10 Hz 的正弦线振动。GPS 的观测频率为1 Hz，并在速度和位置观测中加入速度误差0.01 m/s(1σ)，位置误差1 m(1σ)。EKF 和ST-EKF 的预测频率和更新频率均设置为1Hz。实际上，提高EKF 的预测频率可以改善其估计精度，但是这种方案并不是完全有效的[12]。

为了对比15 状态EKF 和15 状态ST-EKF 的结果，以5 状态（3 个姿态角误差，2 个水平速度误差） EKF精对准的结果作为对比参考值，此时状态是完全可观的。5 状态EKF、15 状态EKF 和15 状态ST-EKF均在3 min 解析粗对准之后开始卡尔曼滤波精对准。由于对准过程中往往航向角是最难估计的，所以这里仅对比观察航向角的收敛结果。EKF 和ST-EKF 的航向角估计结果如图1所示。

图1 单位置精对准EKF 和ST-EKF 的航向角估计曲线 Fig.1 Yaw curves of EKF and ST-EKF in single-position fine alignment

图1表明，在1800 s 以内，5 状态EKF、15 状态EKF 和15 状态ST-EKF 的航向角估计均正常。实际上5 状态ST-EKF 的航向角估计结果与5 状态EKF 结果类似，这里不再过多展示。但是，在1800 s 之后，15状态EKF 所估计的航向角逐渐发散，最终在3600 s 时，15 状态EKF 与5 状态EKF 的航向角差为0.0247°，而15状态ST-EKF与5状态EKF的航向角差仅为0.0009°。

图2 东向陀螺漂移误差标准差曲线 Fig.2 Standard deviation curve of the eastward gyro bias error

图2表明，15 状态EKF 的估计中，东向陀螺漂移误差的标准差是逐渐减少的，而理论上不应该减少。准静态的基座振动环境下，东向陀螺漂移是不可观测的，而且东向陀螺漂移和航向角误差是紧密相关的，由于东向陀螺漂移误差的标准差进行了错误的估计，进 而导致15 状态EKF 的航向角在1800 s 之后发散。但是，15 状态ST-EKF 具有较好的东向陀螺漂移误差标准差估计特性，如图2所示，保持在0.01 (°)/h 附近，所以东向陀螺漂移误差的标准差保持特性使得ST-EKF 的航向角估计不会因为不可观的状态产生错误的校正。

尽管5 状态EKF 在对准过程中不会出现滤波不一致的问题，但是5 状态卡尔曼滤波不适合对准之后的组合导航过程，因为需要通过15 状态组合导航滤波进行初始对准和在组合导航过程中估计陀螺仪、加速度计的零偏误差，提高组合导航精度。当长时间沿直线行驶或停车时，15 状态组合导航滤波误差状态不完全可观。传统卡尔曼滤波在计算方差阵时，由于状态转移矩阵中的比力计算误差，造成方差阵的计算误差，使本来不可观的等效东向陀螺漂移得到错误的修正，从而造成图2的现象。沿直线行驶或停车时间越长，现象越明显。类似现象及描述见文献[4]和[16]。而15状态ST-EKF 适用于对准之后直接进行组合导航，不需要进行滤波状态的切换。

3.2 双位置对准实验

本节进一步通过双位置对准实验来验证ST-EKF的对准性能，包括光纤陀螺IMU 3 min 双位置对准实验和激光陀螺IMU 3 min 双位置对准实验。这里的双位置是指IMU 在一个位置静止80 s 采集数据，再绕天向轴在20 s 内转动180°之后，在另一个位置采集数据80 s，目的是为了提高惯性器件误差的可观测性，提高对准的精度。其中光纤陀螺的零偏优于0.003 (°)/h，激光陀螺的零偏优于0.01 (°)/ h，采样频率均为200 Hz。15 状态EKF 和15 状态ST-EKF 的预测频率和更新频率均设置为1 Hz。重复6 次实验，光纤陀螺IMU 和激光陀螺IMU 的对准结果分别如表2和表3所示。

从表2可以看出，光纤陀螺IMU 的六次实验中，EKF 航向角估计的标准差为0.1170°，而ST-EKF 的航向角估计标准差为0.0238°，ST-EKF 的精度要远高于EKF 的双位置对准精度。从表3可以看出，激光陀螺IMU 实验中，EKF 航向角估计的标准差为0.0382°，而ST-EKF 的航向角估计标准差为0.0209°。

表2 光纤陀螺IMU 双位置对准实验的航向角估计结果 Tab.2 Estimation results of yaw angles in fiber gyro IMU's two-position alignment experiment

表3 激光陀螺IMU 双位置对准实验的航向角估计结果 Tab.2 Estimation results of yaw angles in laser gyro IMU's two-position alignment experiment

两种不同的IMU 系统均表明，ST-EKF 具有更优的双位置对准精度。这是由于在IMU 转动过程中EKF系统矩阵中的比力计算不准确造成了方差阵的估计不准确，影响航向角的估计精度。ST-EKF 则解决了这个问题，航向角估计精度较高，可以在对准之后直接进行组合导航，不需要进行滤波状态的切换。

3.3 激光陀螺IMU/卫星组合导航跑车实验

3.1 节和3.2 节分别从单位置对准和双位置对准实验验证了ST-EKF的优越性能。本节通过激光陀螺IMU/卫星动态跑车松组合导航实验来验证ST-EKF 的性能。激光陀螺IMU 参数如表1所示，IMU 数据输出频率为100 Hz，GPS 输出位置速度频率为1 Hz。跑车轨迹的谷歌地球显示如图3所示。在组合导航过程中，将卫星信号人为取多段进行断开90 s，观察水平位置误差的精度。EKF 和ST-EKF 的预测频率和更新频率均设置为1 Hz，4 h 组合导航的水平位置误差如图4所示。

由图4可以看出，在卫星信号断开的6 个时间段内，EKF 具有比ST-EKF 更大的最大水平位置误差。同时，ST-EKF 的总体水平位置误差曲线都在EKF 的水平位置误差曲线下面。所以，对于导航级IMU，ST-EKF 具有比EKF 更优的组合导航水平位置精度。

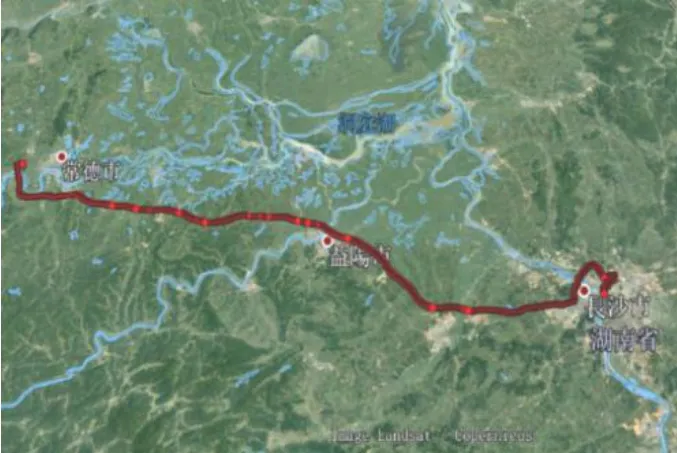
图3 激光陀螺IMU/卫星组合导航实验轨迹 Fig.3 Google curve of RLG-IMU/GNSS integration experiment

图4 激光陀螺IMU/卫星组合导航EKF 和ST-EKF 的水平位置误差对比 Fig.4 Comparisons on horizontal position errors between EKF and ST-EKF of RLG-IMU/GNSS integration experiment

3.4 MEMS-IMU/卫星组合导航跑车实验

为了进一步验证ST-EKF 的组合导航性能，本节设计了STIM300 MEMS-IMU/卫星组合导航实验。STIM300 MEMS-IMU 的性能参数如表4所示。

表4 STIM300 IMU 性能指标参数 Tab.4 Specifications of the STIM300 IMU

IMU 输出频率为200 Hz，GPS 输出位置速度频率为1 Hz。跑车实验时长为3600 s，跑车轨迹的谷歌地球显示如图5所示。EKF 和ST-EKF 的预测频率和更新频率均设置为1 Hz，在完全相同的初始参数设置条件下，EKF 和ST-EKF 的组合导航水平位置误差如图6所示。

图5 MEMS-IMU/卫星组合导航实验轨迹 Fig.5 Google curve of the MEMS-IMU/GNSS integration experiment

图6表明，在多处断开GPS 的情况下，EKF 的最大水平位置误差达到了55 m，而ST-EKF 的水平位置误差均能保持30 m 以下。所以，在3.3 节和3.4 节相应实验中，ST-EKF 不仅适用于导航级IMU 与卫星的组合导航，同时也适用于MEMS-IMU/卫星组合导航。ST- EKF 比EKF 具有更好的动态适应性，导航精度更高。

图6 MEMS-IMU/卫星组合导航EKF 和ST-EKF的水平位置误差对比 Fig.6 Comparisons on horizontal position errors between EKF and ST-EKF of MEMS-IMU/GNSS integration experiment

4 结 论

本文从速度误差定义的坐标系一致性角度，对状态变换卡尔曼滤波的合理性作出了进一步的解释，并推导了捷联惯导的初始对准和组合导航的松组合模型。在状态变换卡尔曼滤波的框架下，组合导航滤波的预测过程不需要以牺牲系统矩阵的高频预测来提高滤波的精度，预测过程和更新过程可以同时执行。同时，对准过程和组合导航过程可以采用统一的15 状态模型，不需要切换组合导航状态，提高组合导航的精度和稳定性。

激光陀螺IMU 的动基座单位置对准实验验证了状态变换卡尔曼滤波具有比传统扩展卡尔曼滤波更好的航向估计稳定性和精度。激光陀螺IMU 和光纤陀螺IMU 双位置对准实验亦验证了状态变换卡尔曼滤波具有比传统滤波更高的对准精度。

激光陀螺IMU/卫星组合导航实验表明，在多处卫星信号断开的情况下，状态变换卡尔曼滤波比传统的滤波方案定位精度更高。MEMS-IMU/卫星组合导航实验验证了，在多处卫星信号断开的情况下，传统卡尔曼滤波的最大水平位置误差达到了55 m，而状态变换卡尔曼滤波的水平位置误差均在30 m 以下。