基于排队评分法与矩阵分析法的多指标再生混凝土力学性能的优选研究

唐佳军， 裴长春

( 延边大学 工学院， 吉林 延吉 133002 )

近年来，一些学者对再生混凝土(RAC)进行了正交试验研究.例如，金宝宏等[1]以再生骨料(RA)替代率、粉煤灰(FA)替代率和钢纤维(SF)掺入率为因素，以坍落度、抗压与劈拉强度为指标，通过极差分析与点图分析对研究指标进行了正交试验研究.孙呈凯等[2]以RA替代率、FA替代率、水胶比和PVA纤维掺入率为因素，通过对正交试验结果进行层次分析、方差分析与因素指标分析，研究了各因素对RAC的抗压与劈拉强度的作用规律.张学兵等[3]设计了一种3因素、4水平、3指标的正交试验方案，利用直观分析、极差分析、层次分析、因素指标分析和方差分析研究了RAC的最佳强度组合与因素指标的关系.由以上研究可以看出，目前正交试验方案中的分析方法较为复杂.研究表明，采用排队评分法[4]或矩阵分析法[5]时仅需对评分总和或试验指标进行极差分析，可以大大减少工作量，提高分析效率，但目前该方法多应用于机械设计制造等方面[6-8]，在RAC的正交试验分析中的应用尚未见报道.基于此，本文在文献[9]研究的基础上，以RA替代率、FA替代率和SF掺入率为因素，抗压强度、劈拉强度、抗折强度、拉压比与折压比为指标，分别利用排队评分法与矩阵分析法研究多指标情况下RAC的最佳组合方案，以期为RAC的正交试验研究提供理论参考.

1 试验概况

设计3因素、4水平、5指标的L16(43)正交试验方案，试验因素与水平见表1，其中因素A、B、C分别表示RA替代率、FA替代率和SF掺入率.试验原材料、配合比、试件制备与具体试验方法详见文献[9]，RAC各指标(28 d抗压强度、劈拉强度、抗折强度、拉压比与折压比)的测试结果见表2.

表1 试验因素与水平

表2 RAC各指标的测试结果[9]

2 排队评分法的计算

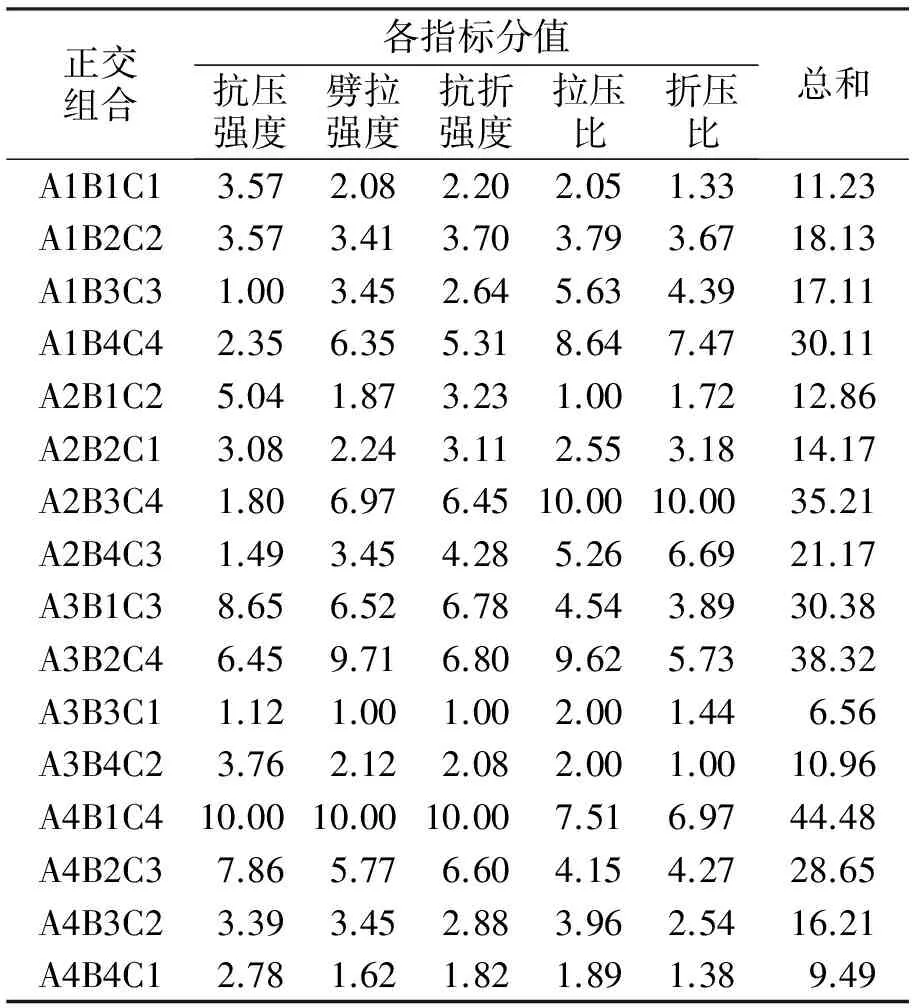
排队评分法首先依据测试结果在单个指标中的排序对测试结果进行评分，然后对各指标下的分数求和，从而把多指标问题转化为单指标问题.评分总和越高，表明组合越优.本文将各指标下的评分最大值定为10分，最小值定为1分，其他值根据内插法[10]确定分数.考虑到计算量较大，采用Spss软件进行内插法的计算，计算结果见表3.由表3可知，各试验组中第13组的评分最高，即结果最优，这与文献[9]中的分析结果相同.

评分总和的极差分析结果见表4.由表4可以看出：各因素对试验指标影响的大小顺序依次为C>B>A，即SF掺入率>FA替代率>RA替代率；RAC的最优组合为A4B2C4，即RA替代率为100%、FA替代率为10%、SF掺入率为1.8%.文献[9]的结果表明：各因素对劈拉与抗折强度影响的大小顺序依次为SF掺入率>FA替代率>RA替代率，而各因素对抗压强度影响的大小顺序依次为FA替代率>RA替代率>SF掺入率；RAC的最优组合为A4B1C4.由以上可知，排队分析法所得结果与文献[9]的结果有所不同，其原因为： ①排队评分法在确定评分最大值与最小值时易受主观判断的影响； ②文献[9]中的指标仅考虑了强度，而本研究除了考虑强度还考虑了拉压比与折压比.

表3 排队评分法的计算结果分

正交组合各指标分值抗压强度劈拉强度抗折强度拉压比折压比总和A1B1C13.572.082.202.051.3311.23A1B2C23.573.413.703.793.6718.13A1B3C31.003.452.645.634.3917.11A1B4C42.356.355.318.647.4730.11A2B1C25.041.873.231.001.7212.86A2B2C13.082.243.112.553.1814.17A2B3C41.806.976.4510.0010.0035.21A2B4C31.493.454.285.266.6921.17A3B1C38.656.526.784.543.8930.38A3B2C46.459.716.809.625.7338.32A3B3C11.121.001.002.001.446.56A3B4C23.762.122.082.001.0010.96A4B1C410.0010.0010.007.516.9744.48A4B2C37.865.776.604.154.2728.65A4B3C23.393.452.883.962.5416.21A4B4C12.781.621.821.891.389.49

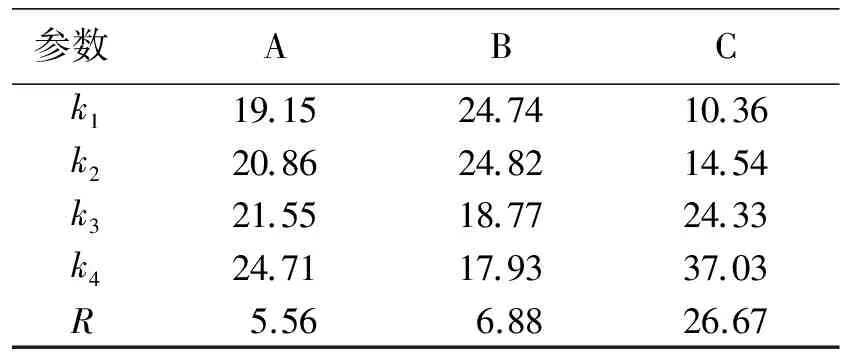
表4 评分总和的极差分析结果

注：ki为各因素i水平评分总和之和的平均值，R为极差.

3 矩阵分析法的计算

矩阵分析法不是直接利用各试验组的测试结果，而是通过设置权矩阵的形式对数据进行客观分析[9].其计算过程如下：

1)建立层次结构模型.层次结构模型通常.建立一个由指标层、因素层和水平层构成的3层递阶层次结构模型，如图1所示.

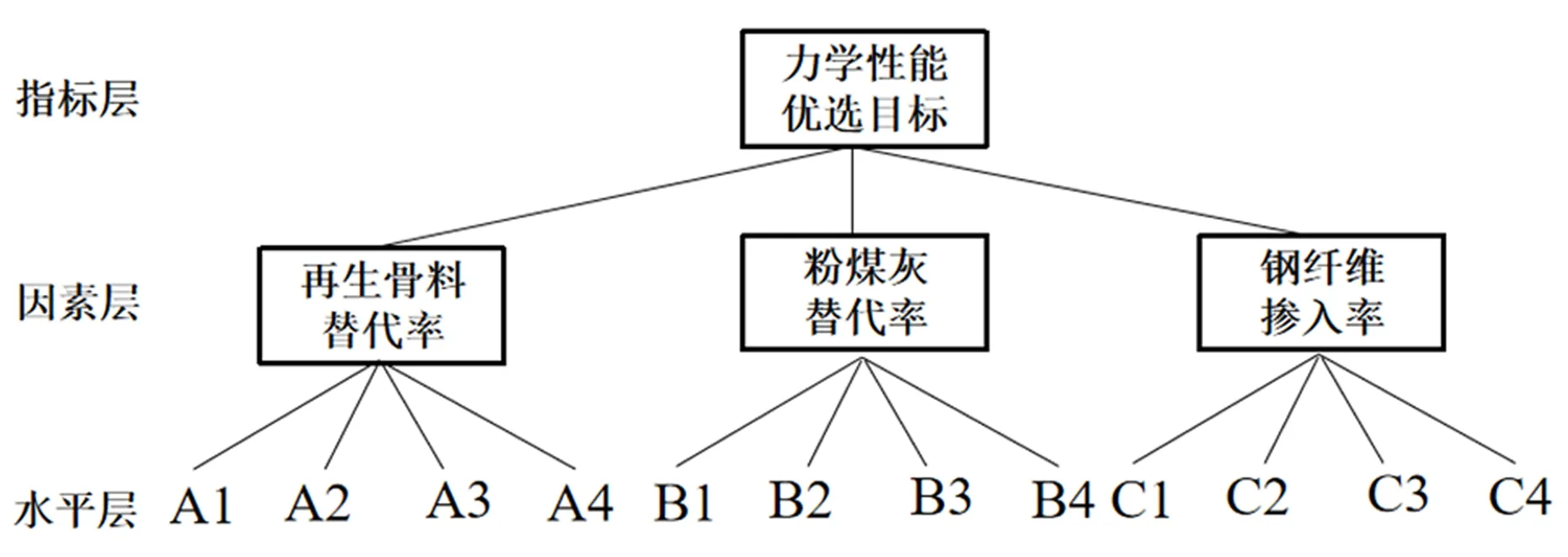
图1 层次结构模型

2)建立矩阵.指标层矩阵M由各因素各水平下试验指标的平均值Ki j(或平均值的倒数1/Ki j)组成，其中i代表因素，j代表水平.若指标数值越大越好，则矩阵M中的数值取平均值Ki j；反之取其倒数1/Ki j.因素层矩阵T由同一因素下各水平的试验指标之和的倒数构成.矩阵M与T的乘积表示单个水平在因素内的影响程度.水平层矩阵S由同一指标下各因素的极差与极差之和构成，S矩阵表示单个指标下各因素的影响程度.将指标层矩阵M、 因素层矩阵T与水平层矩阵S连续作乘法得到矩阵W， 矩阵W表示各因素各水平对各指标影响权重的集合.对于m因素n指标的正交试验研究，各矩阵如式(1)—式(3)所示.

(1)

(2)

(3)

3) 计算矩阵.本文以抗压强度这一指标为例，利用Matlab软件对矩阵分析法的计算进行说明.表5所示为抗压强度的极差分析结果，将表5中的值以矩阵的形式编程输入Matlab窗口运行，以此求解各因素水平对试验指标影响的权重值.具体矩阵见图2.

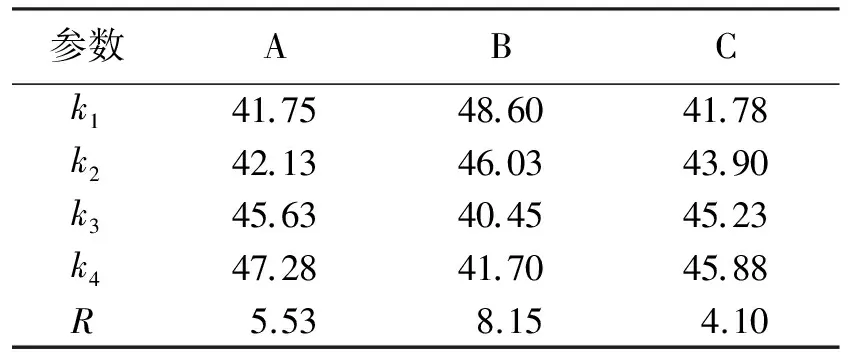
表5 抗压强度的极差分析结果

图2 输入Matlab的具体矩阵

利用以上方法分别对其他指标进行矩阵分析，并对所得结果求和，结果见表6.由表6可知，RAC的最优组合为A4B1C4，即RA替代率为100%、FA替代率为0%、SF体积率为1.8%；各因素对试验指标影响的大小顺序依次为SF掺入率(C)>FA替代率(B)>RA替代率(A).以上结果表明，采用矩阵分析法所得的结果与文献[9]的结果更为接近.

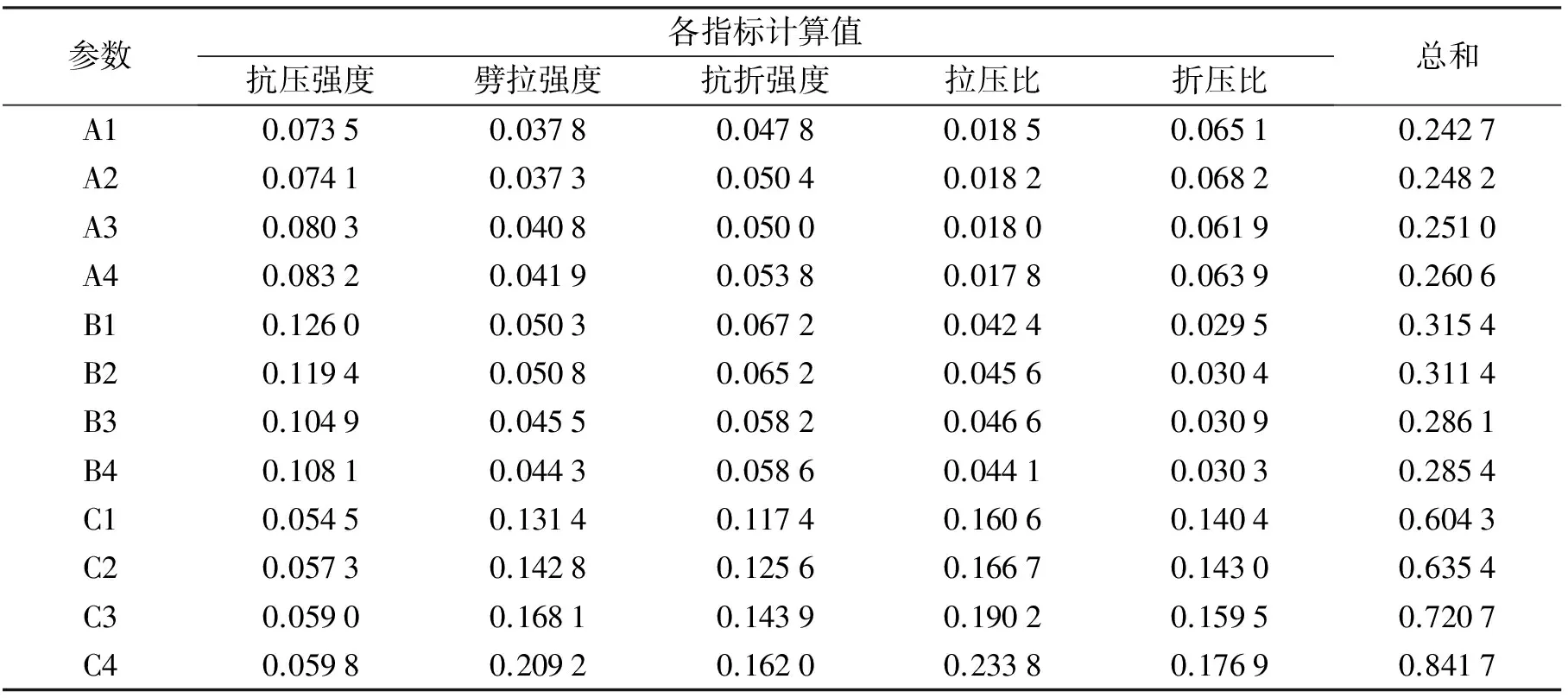
表6 采用矩阵分析法对各指标的计算结果

4 结论

本文以RA替代率、FA替代率和SF掺入率为因素，抗压强度、劈拉强度、抗折强度、拉压比与折压比为指标，分别利用排队评分法与矩阵分析法研究RAC力学性能的最优组合.结果表明： ①各因素对RAC力学性能影响的大小顺序依次为SF掺入率>FA替代率>RA替代率.②排队评分法计算得出的RAC力学性能的最佳组合为A4B2C4，矩阵分析法计算得出的RAC力学性能的最佳组合为A4B1C4.考虑到使用粉煤灰可节约水泥用量且环保，因此在实际应用中FA替代率应取为10%(因素B选取水平2).③本研究显示，矩阵分析法所得结果与正交试验分析的结果更为接近，由此表明矩阵分析法在确定最佳组合方案时优于排队评分法.