让思想在课堂里涌动

尹宇

摘 要：随着素质教育的提出，现下教学越来越注重培养与提升学生的综合素养。小学阶段，学生的思维处于发展的活跃阶段，此刻展开的教学与引导是学生以后学习与发展的基础。小学数学中存在着很多的数学思想，这些数学思想是数学知识的精髓与灵魂，在实际教学中教师要合理利用科学的教学方式渗透数学思想。探讨小学高段空间图形学习的现状，分析学生在学习空间图形过程中存在的问题，并在此基础上探讨在小学数学高段空间图形中渗透数学思想的重要性，以及探究小学数学高段空间图形中渗透数学思想的教学策略，以此作为小学数学空间图形教学中渗透数学思想的参考依据，旨在提升小学数学空间与图形的教学质量与效率。

关键词：小学数学;空间与图形;数学思想

数学知识主要由概念、性质、法则、公式、数量关系、解题方法构成，但是数学并不是这些简单的组合，数学还涉及较多的数学思想与方法。数学思想，即人们在数学知识的学习过程中对数学理论与内容的本质认识，是从理论知识中提炼出来的具备更高层次水平的观点，是数学普遍规律的一种揭示，关系与影响着数学的实践活动。另外，数学思想以数学知识为载体，并超脱数学知识，是一种运用数学知识合理解决实际问题的能力与方法。在实际教学中，教师要注重在教学中渗透数学思想，引导学生真正领悟数学知识，培养与提高学生应用数学知识解决实际问题的能力，为学生更好的发展与提升打下良好的基础。

一、小学生空间图形学习的现状

在小学生空间图形教学中，理论教学知识占据的比重过大，受其身心特点的影响，学生对理论知识并不是特别感兴趣，相应的学习效果可想而知。此外，教师的课堂教学方式单一，一些教师依旧使用传统灌输式教学方式传授教学知识，不利于学生思维的发散与培养，阻碍学生空间想象能力的提升与发展。在实际教学中，教师忽略教学主动，没有在教学中调动学生的积极性与主动性，很多学生处于被动学习的状态，致使学生逐渐丧失学习兴趣。

二、小学数学思想方法在高段空间与图形教学中渗透的重要性

在小学高段“空间与图形”教学中渗透数学思想，不但能促使学生理解与掌握相关数学知识与基本技能，还在一定基础上有利于拓展学生思维，启发学生智力，实现学生自身潜能的挖掘以及培養学生思想道德品质与非智力因素。数学思想的渗透可以帮助学生建立更强的数学观念，促使学生在学习的过程中养成良好的思维素质，更好地实现素质教育。小学数学知识重要，数学思想更为重要，这两点是小学数学教材中重要的主线。在数学思想的渗透下，数学知识不再是简单的概念与性质记忆，数学方法也不再止步于单一的教学方式，可以实现学生对教学内容的整体把握。小学数学教学应该紧随时代发展，适应国际数学教学发展以及社会发展。在小学数学中渗透数学思想，有助于提升学生的综合素养，为学生以后在社会中的发展打下良好的基础。并且，小学数学高段空间与图形教学知识相互独立与密切联系。数学思想的渗透可以加强相关数学知识的联系，引导学生举一反三，培养学生的创新思维，帮助学生融会贯通所学的数学知识，还有助于学生第三学段学习的过渡。

三、在高段空间与图形教学中渗透的数学思想

（一）极限思想

这种数学思想主要是引导学生从有限认识无限，教导学生如何借助近似深刻认识精确的概念，是数学思想中一种重要的思想方法，是事物转化的重要环节，掌握这种思想对学生的发展有着重要的意义。

（二）化归思想

作为解决数学问题的重要思想，这种思想是指将待解决的问题转化为较为简单的问题，轻松解决。在现实世界中，事物不是恒定不变的，而是不断变化的，应用这种思想可以有效简化数学问题的解决步骤与过程。

（三）数形结合思想

作为数学教学研究对象的两个侧面，数与形有效地结合空间形式与数量关系，将与之相关的问题综合起来分析与解决。在空间与图形教学知识学习时，运用这种思想可以有效找到问题的关键，迅速找到解决问题的钥匙。

（四）符号化思想

在空间与图形中，需要用符号代表图形中的顶点，如果没有符号的统一标注，在实际问题解决中就会显得十分复杂与杂乱，导致数学知识成为“天书”，因此符号化思想的渗透是十分重要的。

（五）集合思想

将具备相同特质的事物组合成一起，划分为同类，这种思想是现代思想的基础，在小学数学教学中多处体现。

四、在高段空间与图形教学中渗透数学思想的方法与案例

（一）建立数学模型，合理应用学生的想象力渗透数学思想

在空间与图形学习中，空间想象能力发挥着重要的作用，在实际教学中，空间想象主要依赖空间感知，教师要合理激发学生的空间想象思维，锻炼学生的空间想象能力，实现学生空间观念的提高。比如：在直线的无限性质教学时，教师除了可以在教学中进行线段、直线、射线的比较，讲解有关直线、射线、线段的概念与知识外，还要讲解在真实的世界中并没有直线与射线，而是人们在脑海中想象并规定的一种数学工具。这种概念的提出是为了数学计算与问题解决的方便。然后，教师可以引导学生想象直线的特征，引导学生在头脑中塑造直线的模型。在此过程中，教师一定要强调无限延伸，促使学生在脑海中绘制出本质上的直线，并在此过程中渗透相应的极限思想。

（二）合理设置练习，引导学生通过习题感悟数学思想

在实际教学中，教师会发现这样一种状况：给学生讲解的习题种类很多，但是学生的解题水平仍停留在套用的阶段，题干条件稍微出现变化，就会导致学生手忙脚乱，这种状况下学生不会行成良好的解决问题的能力，更不会产生创新能力。导致这一情况出现的原因主要是由于教师在教学中没有引导学生感悟数学思想与数学方法，只是让学生对相关知识进行记忆。为此，在实际教学中，教师要合理设置练习题目，引导学生通过练习进行数学思想的感悟。比如：在图形面积相关知识讲解时，教师可以为学生设置下面一个问题。

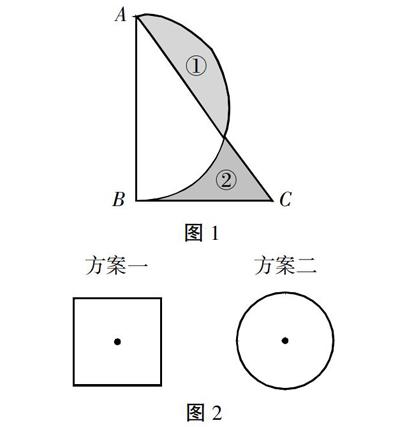
如图1所示，三角形ABC是直角三角形，AB=4，BC=3，求阴影部分①与阴影部分②的面积相差多少？

通过题干与图的观察，可知阴影部分②的面积与空白部分图形的面积之和与三角形的面积相等，阴影部分①的面积与空白部分的面积之和等于半圆的面积。经过分析，从而可以将面积之差转化为三角形与半圆面积之差，从而减少计算，简化过程。

（三）课后总结，在引发学生质疑与反思中渗透数学思想

在教学中，教师要引导学生进行反思与质疑，并提出自己独特的见解，实现教学质量的提升。如在圆锥体积公式推导教学时，教师可以先提出有关问题引发学生思考与猜测，并引导学生对自己的猜测进行操作验证，从而对实际问题进行验证，并在这一过程中推导出相应的结论。应用转化思想，合理将圆锥面积的求解转化为三角形与圆弧面积的求解。这一教学过程中，学生会由于好奇心理与质疑心理对探究的内容产生浓厚的兴趣，并在验证过程中体会到学习数学知识的乐趣，在推出结论后，学生体验到转化思想与数形结合思想的妙用。

再比如：在“圆的认识”相关内容教学时，教师可以引入一个问题“某班举办套圈活动，套圈方案有两种（如图2），同学们认为哪种方案更为公平？”引发学生展开讨论与思考，总结四边形与圆形的相关知识，并以此渗透相应的数学思想。在讨论过程中，学生会认为方案二更为公平，因为离圆心的距离是相同的，教师可以通过多媒体课件为学生演示无数个点组成圆的过程，以此渗透集合数学思想。

参考文献：

[1]李银银.小学高段“空间与图形”教学中数学思想渗透策略探讨[J].新课程（小学），2016（1）.

[2]高海兵.浅谈如何在小学数学教学中渗透数学思想方法[J].数学学习与研究，2016（12）：53.

[3]冯莉.浅谈如何在小学数学课堂中渗透数学思想方法[J].中国校外教育，2017（5）：127.

编辑 王 敏