能量理论在空空导弹攻击效果评价中的应用*

孙庆鹏，李战武，寇英信

（空军工程大学航空航天工程学院，西安 710038）

0 引言

随着航空工业的飞速发展，飞机装备性能的不断进步，中远距空空导弹的使用，超视距空战［1］成为现代空战的主要形式。但随之而来的，是由于导弹飞行时间的增加，导致飞行员长时间得不到攻击效果的信息反馈，给下一步的战术决策带来困难。

对于飞行员而言，其在一次完整攻击过程中真正需要的，是能够及时了解攻击效果与敌我状态，在此基础上飞行员可以更好地进行决策。如当载机发射导弹后，若目标的机动量很大，则可判定此次攻击失败，需要进行PK［2］（杀伤概率）增强射击；反之则攻击成功，载机进行下一个任务。而这就需要比较导弹追踪段内目标的机动量与导弹的最大允许机动量，目前有很多评估空空导弹攻击效能的理论［3-5］，但多数都是从导弹的运动方程出发［6］，对能量的考虑有所欠缺。基于上述原因，本文提出机动强度用以描述一段时间内飞行器的能量消耗，并以此来判断空空导弹的命中结果。然而，在空战中战斗机发射导弹的目的不单单只有毁伤目标，还包括迫使目标机动，便于载机机动占位，特别是在发射区远边界处发射的导弹，其更多的目的是后者。机动强度能够评价前者的效果，但却不能体现后者带来的优势。为了更全面地评价导弹攻击效果，本文提出机动潜力用以描述目标的剩余机动能力，并以此来评价导弹攻击带来的机动优势。

1 机动强度

1.1 机动强度的重要性

导弹追上目标，归根到底是靠能量差。从能量机动的角度来说，只有导弹的单位剩余能量高于敌机，才有可能追上敌机，因此，从能量角度对导弹攻击过程进行分析是不可或缺的。而对导弹攻击效果的分析，即机动强度的重要性有如下几点：

1）现代战斗机发展趋向于高隐身性能，导弹多为内置式，即便加装了保形弹舱，其载弹量也十分有限。若对一架本就可以击中的目标进行重复射击，就会浪费弹药，影响连续作战能力，延缓对友机的支援速度。2）当首次攻击不能对敌机造成有效打击，若不及时进行PK 增强射击，就可能被敌机反击，失去原有优势。3）在防御性防空中，若首次攻击失效，而战斗机又不能对攻击结果进行预判，就无法及时拦截/摧毁目标，就会被敌机突破封锁，从而导致需保护的己方单位遭受攻击。4）当载机所受威胁增大，通过对攻击效果的判断，可放弃制导中的导弹并进行机动，降低自身受到的威胁。

1.2 机动强度概念

机动强度是用于对导弹命中结果进行评价，因此，其表征的是有关导弹能否有效跟踪/攻击目标。因此，机动强度应从导弹追踪目标的特点出发描述机动量。

导弹防御原则［7］。一是不论是否看到敌机，要遵守的原则：与最紧急的威胁交战。飞行员会面临许多情况，为了提高生存率，必须优先对付最迫在眉睫的威胁。例如：在你尾部的敌机发射了红外导弹，此时敌机不再是最大威胁，导弹才是最大威胁，必须先应付导弹。二是用相对航向角（双方航向的夹角）对付导弹。当导弹飞向你，要尽快转弯，使导弹在你的3/9 线上，给导弹制造最大的制导难题。导弹要击中你需要按照提前量飞行，而你这样就使导弹的提前量最大。而且你会以最大视线率穿越导弹导引头的视场，图1 显示了这样的情形。

根据飞机防御导弹的原则，可知转弯是对付导弹最基本也是最有效的方式。但现有的评价方法并不能有效体现转弯对导弹攻击效果的影响，主要是因为单纯从运动学角度出发，没有考虑转弯时能量损耗与过载的关系。为了正确分析飞机转弯对导弹的影响，需要一个能够用来比较双方机动大小，准确评价转弯影响的物理量，即机动强度。

与计算单发导弹的杀伤概率［8］相比，机动强度的作用不仅体现在攻击过程中，还体现在防御过程中。在以往的导弹防御机动中，飞行员只能依靠自身经验来确定下一步采取何种机动，但不同类型的导弹与发射时状态的不同，导致其在末制导段的机动性能也不同，想要建立可靠的经验十分困难。若载机机动过小，就会被导弹命中；若载机机动过大，就会导致失去过多能量，不利于下一步的作战。而通过计算载机和导弹的机动强度并进行比较，定量分析防御导弹攻击所需的机动大小，有利于飞行员选择合适的机动动作与幅度。

1.3 机动强度模型

战斗机有两种类型的能量：动能和势能。动能只涉及飞机飞行的速度，势能则是可以“储存”起来转化成动能的能量。飞行员可以通过改变机头指向来转换能量，任何时候，飞机作机动或转弯会“消耗”能量。由于导弹的主要机动只有两种，直行与转弯，且直行时所受的空气阻力能够根据速度与所在高度查表获得，能量消耗也就能够对应确定。因此，本文主要讨论转弯对能量消耗的影响。当飞行员执行一个高G 的转弯，飞机将会“浪费”或丧失更多的能量，因此，能量消耗大小应与Gf值相关。

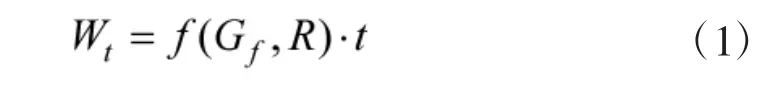
式中，Wt为转弯消耗的能量；R 为转弯半径；t 为以过载Gf转弯所用时间；f 为能量消耗与转弯Gf值的关系，与飞机自身性能（翼载等因素）有关。对于信息充足的己方飞机，可通过计算式（2）中的反函数确定；而对于敌机而言，由于缺少足够的数据，可使用在线学习［9-10］的方式确定，这里选择适应正则化学习［11］，这是因其能在剔除异常值的基础上，不断利用新数据进行更新，增强函数的可靠性。

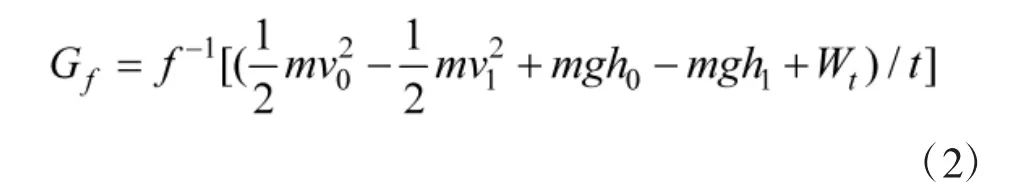
式中，v0为转弯前速度；v1为转弯后速度；h0为转弯前高度；h1为转弯后高度；m 为飞机质量；Wt为转弯过程中，燃料燃烧转化的飞机机械能。

设目标机速率为Vm，则有

式中，g 为地心引力；Gm是目标转弯时的过载。载机的G 力可以通过机载传感器获得，但目标机和导弹的G 值无法直接获得，只能通过上式进行计算。

根据式（3），将飞机减慢到最低空速并尽可能地拉杆（增加G 值）是获得高转弯速率的最好的方法。但实际上，G 值也受到空速的影响。如图2（a）、（c）所示，在较低的空速下，飞行员只能施加较少的G 值，也就是说，当飞机变慢时，飞行员不能无限制地施加G 值。在较低的空速下，机翼所产生的升力也较小，结果，导致了更少的施加G 值的可能性。

设目标机直行段能量消耗为WS，则最终目标机动强度S 可表示为：

设目标飞行时间为ta，则目标在这段时间内的平均机动强度可表示为：

令ta=1，可求得目标的瞬时机动强度，反映目标在某一时刻的运动剧烈程度。再结合成功防御导弹所需的平均机动强度，即可令飞行员大致确定所需采取的机动动作与幅度。

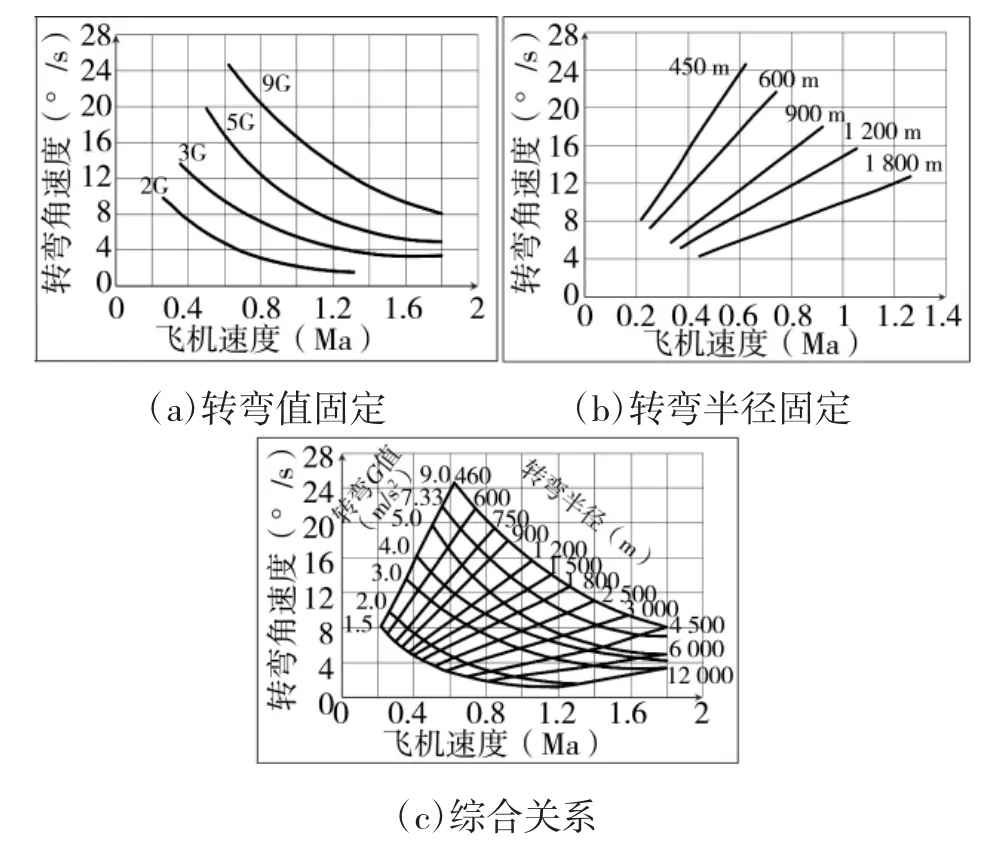
图2 转弯性能随转弯G 值和转弯半径的变化曲线

确定目标成功防御导弹时所需的机动强度大小，就需要了解导弹命中目标所需的能量大小，即需要计算导弹的机动强度。由于导弹燃料的燃烧时间很短，若从较远距离处发射，其末段速度会变得很小，当其与目标的相对接近速率为负值时，就再也无法追上目标；另一方面，当导弹速度小于最小可控速度时，也视为无法追上目标。因此，将二者中较大的一个作为限制条件。导弹的运动轨迹可以根据目标运动轨迹和导弹的制导率确定，但其速度大小却无法直接测量，本文通过能量守恒定律对其进行计算。

设导弹发射初速度为vd0，高度为hd0，初始质量为md0，则预计命中时刻导弹具有的机械能Wc为：

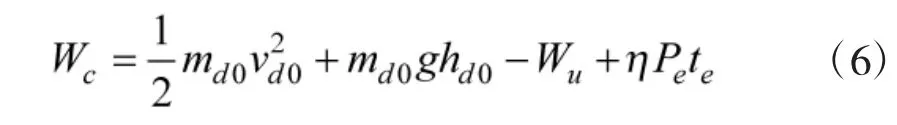
式中，Wu为导弹飞行过程中消耗的能量，即导弹的总机动强度，Wu=Wd+Wz；Pe为燃烧燃料释放内能的功率，与大气密度有关，可以根据导弹所在海拔高度确定［12-13］；te为燃料燃烧时间，当导弹飞行时间t>燃料最大燃烧时间temax时，取te=temax，否则取te=t；η为燃料内能转化为导弹机械能的效率，与发动机性能有关。由于导弹在直行段受到的空气阻力可以根据导弹速度实时计算［14-15］，因此，导弹在直行段的能量消耗Wz容易计算，只需再计算转弯时的能量消耗Wd即可。

由于导弹是根据一定导引规律对目标进行跟踪，因此，目标的转弯应与导弹的转弯有直接联系，也就能够从目标的机动强度推断导弹的机动强度。

设导弹与目标的相对距离为L，相对高度差距为hc，目标机执行一个半径为Rm、速度为Vm的转弯机动，则导弹转弯的需用过载Gn为：

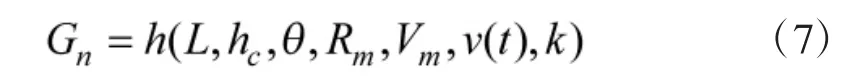
式中，k 为比例导引法的比例系数；θ 为双方相对航向角；v（t）为t 时刻导弹速度大小，h（）可根据文献［16］中的式（6）确定。

设导弹的可用过载为Ga，则实际过载Gd为：

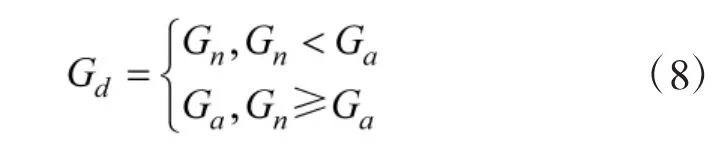
再根据导弹转弯时能量消耗与G 值的关系p（仿照式（2），根据实验数据拟合其反函数确定），可得导弹以过载Gd转弯过程中的能量消耗Wd：

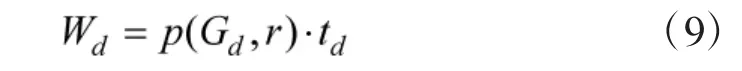
式中，td为以过载Gd转弯所用时间；r 为导弹以过载Gd转弯时的转弯半径，可利用速度与过载根据式（3）计算，p（）为能量消耗与转弯Gd值的关系，与f（）确定方法相同。假设需用过载始终不大于可用过载，则根据转弯前后的能量守恒有：

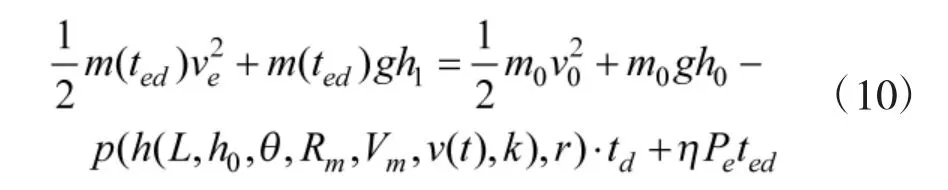
式中，m（ted）为燃料燃烧后的导弹质量；ted为转弯过程中燃料燃烧的时间。

将所有常量之和设为T，则转弯后的速度Ve为：

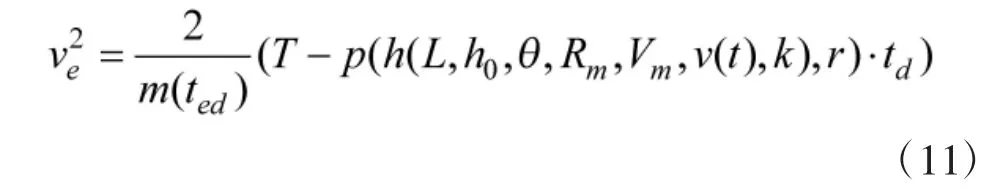
当时间步长很小，燃料燃烧导致的质量变化可忽略不计，此时有：

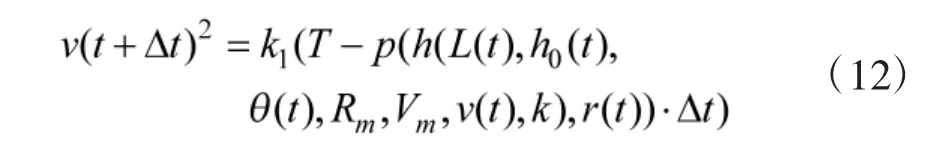
最后联立式（1）、式（4）、式（6）与式（12），解算转弯过程中导弹机动强度M 与目标机动强度S 的关系为：

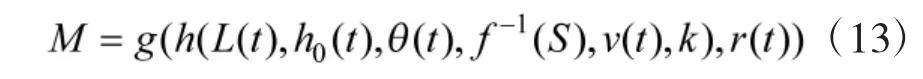
式中，g（）为根据转弯过程数据对式（12）进行积分并带回式（4）与式（6）的过程。再以导弹末速度=max（目标速度，最小可控速度）为条件反推，可得恰好能够成功命中目标时导弹的机动强度，再根据式（13）反推，可得目标机动强度阈值。对于进入主动段的导弹而言，一旦目标脱离其导引头视场范围［17-18］，就无法继续追踪目标。因此，还需在进行式（12）的递推时，需要对双方相对航向角进行判断，一旦其超过限制值，就判定攻击失败。

2 机动潜力

如果只考虑对导弹进行防御，那么机动强度越大越好，但飞机在高机动强度的动作后，其剩余机动能力即机动潜力就会大幅削弱，即陷入机动劣势。为了尽量保留剩余机动能力，合理规划逃逸导弹所需的机动强度，还需对机动潜力做出合理评价。不论是博伊德的能量机动理论，还是战斗机的敏捷性指标［19-20］，它们表征更多的是战斗机本身固有的性能，与飞机实际状态无关。而本文中的机动潜力则是描述当前时刻空战双方相对潜在机动能力的物理量，其与飞机性能、当前时刻状态，以及双方相对位置关系都有关。因此，其体现的应该是当前时刻载机与目标之间的相对关系，本文从3 个方面出发，以载机为参照物，确定目标的机动潜力。

目标的机动潜力fp 可表示为：

式中，fp 为相对机械能；fs 为相对SEP；fv 为指向速率比。

机动潜力的评价指标与非参量法进行态势评估的指标［21-26］相似，但其包含的意义不同。态势评估是对当前状况的比较，而机动潜力则是双方蕴含的潜能，是对未来可能性的比较，根据飞行员的机动选择，发挥的机动潜力也不相同。

2.1 相对机械能

机械能是飞机动能与势能之和，代表当前时刻飞机蕴含的能量。再优秀的飞行员，也无法用缺乏能量的飞机进行复杂的机动，导弹的战术攻击区也与飞机能量息息相关。

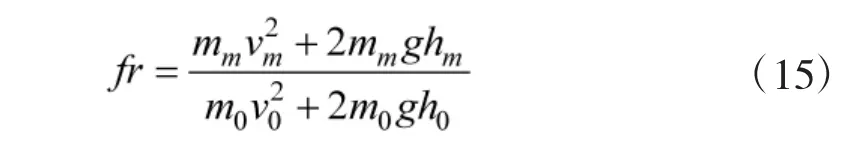
式中，mm、m0分别为目标和载机的质量；vm、v0分别为目标和载机的速度；hm、h0分别为目标和载机的高度。

2.2 相对SEP

在飞机失去动能后，不仅可以降低高度将势能转化为动能，也可以依靠一段时间的直线飞行，将燃料的内能转化为自身动能。SEP［27-28］（specific excess power，单位剩余功率）就是定量描述飞机这一性能的指标，其定义为在给定的油门状态下，飞机能量高度在飞行过程中随时间的变化率。SEP 越大，飞机的加速性能与爬升性能越好。

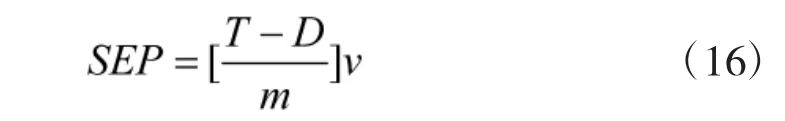
式中，T 为瞬时推力；D 为瞬时阻力；V 为瞬时速度；m 为飞机质量。目标机的推力无法直接获得，但可以通过测量目标的加速度am确定其SEP。则双方的SEP 比为：

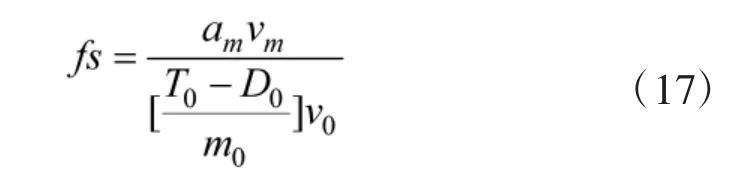
2.3 指向速率比

仅从机械能来描述飞机机动潜力，就无法对角度战术、特别是过失速机动［29］的优势进行很好的解释。而实际上，角度之中也包含着能量关系。因此，本文参考空战双方的指向裕度，提出指向速率比，对双方在角度上的机动潜力进行衡量。

指向裕度［30-31］是衡量空战敏捷性的指标之一，它能够评估飞机指向目标的快慢程度。指向裕度定义为被指向方机头指向线与指向方机头指向线之间的夹角。如图3 所示，即表示当我机开火时，敌机需转动多少角度才能指向我机。但在空战中，双方都会尽力避免被对方机头指向己方，图3 的情况很难发生，因此，利用目标进入角和提前角，提出指向速率比，比较双方指向对方的快慢程度。图4 显示了目标进入角与提前角，显然，图4 的情况更具有一般性。当指向速率比大于1 时，代表目标机指向载机比载机指向目标机的速度快，即若保持当前运动状态，目标机能够更快获得角度优势。

式中，fv为指向速率比；q 为目标进入角；为提前角；w（vm）、w（v0）分别为目标和载机根据当前速度计算出的最佳转弯速率，可根据当前速度与图2 确定。

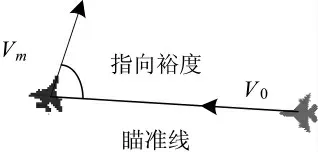
图3 指向裕度

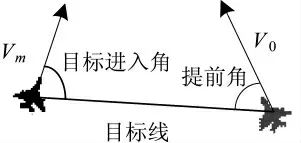
图4 目标进入角与提前角

3 仿真分析

设初始状态载机与目标相对距离为40 km，载机速度为300 m/s，匀速直线飞行，双方迎头飞行，假设双方飞机性能相同。导弹的最大射程为40 km，载机已发射一枚导弹，且目标和导弹相对距离为20 km，目标速度为300 m/s，导弹当前速度为600 m/s 且燃料已耗尽，导引规律采用比例导引法，且比例系数为3，导引头视场角为±30°，杀伤半径为10 m，阻力系数取0.2，其与目标的初始相对航向角为180°，在同一水平面内，目标机以0.05 rad/s 的角速度进行匀速转弯。

在不考虑能量因素，只根据导弹数学模型（运动模型、导引率模型等）分析的情况下，导弹将在35.09 s 时，于（14 087 m，7 087 m）处击中目标，预计目标与导弹的运动轨迹如图5 所示。

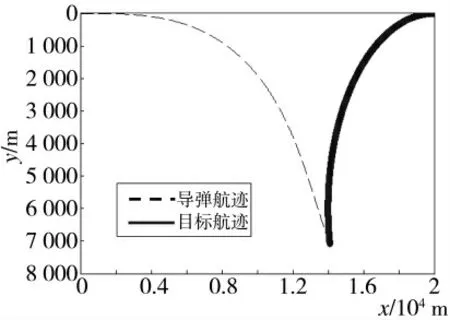
图5 纯数学模型轨迹图

但如果考虑能量因素的影响，则目标在这段时间内的平均机动强度为：

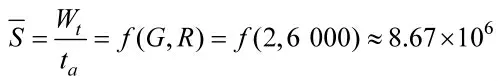
而将导弹运动代入式（12）反推可知成功防御时的目标平均机动强度阈值为6.85×106，由于8.67×106＞6.85×106，因此，目标机动能成功防御导弹。为了进行验证，利用导弹机动强度计算其预计命中时刻速度。

由于导弹的转弯过载与速度在不断变化，因此，计算机动强度时需采用微元法，步长取0.01 s。

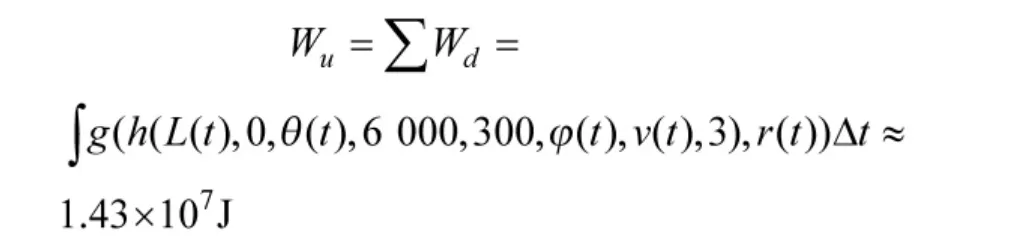
根据导弹机动强度可以确定其命中时刻速度为：

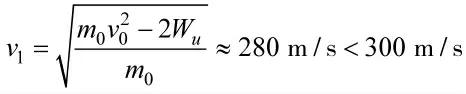
因此，可知导弹无法命中目标，利用机动强度计算的目标与导弹轨迹如下页图6 所示。

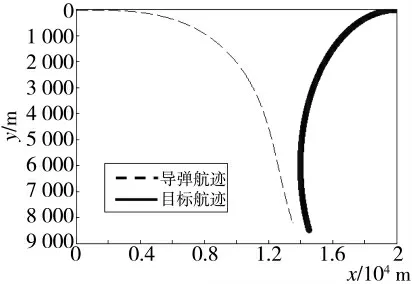
图6 考虑能量因素运动轨迹图

再计算目标机动前后的机动潜力：

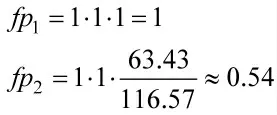
分析结果发现虽然目标没有进行大过载机动，使其相对机械能与SEP 并未改变，但由于其为躲避导弹进行转弯，在角度上陷入劣势，从而导致机动潜力减小。

4 结论

本文从导弹追踪目标的特点出发，从能量的角度研究飞机躲避导弹的基本原则，提出了机动强度，推导了导弹与目标运动强度的对应关系，弥补了现有方法对转弯过程中能量消耗考虑不完备的缺点，给导弹攻击效果评价提供了新的思路。同时，结合大机动强度会影响飞机后续机动的情况，又提出机动潜力，对敌我双方剩余机动能力进行比较，为下一步战术的选择奠定基础。仿真结果证明使用机动强度能够弥补仅仅使用运动方程评价导弹攻击效果的缺陷，机动潜力能够较好地体现进行大机动强度的动作后对机动潜力的影响，比较符合空战实际。本文没有考虑目标释放干扰弹后对导弹的影响，这方面还有待进一步研究。