一种迷彩伪装效果评价指标权重分配算法*

李中华，喻 钧⋆，胡志毅，代 军，张文琪

（1.西安工业大学计算机科学与工程学院，西安 710021；2.陆军研究院工程设计研究所，北京 100043）

0 引言

现代战争中，迷彩伪装是提高伪装目标战场生存能力的关键技术。无论是普通迷彩还是近年来快速发展的数码迷彩，迷彩伪装效果的好坏对于伪装目标的战场生存能力有着重要影响。伪装效果评价目前常常采用单一指标或多指标综合评价，多指标中的权重分配一般采用平均分配或专家评判［1-6］的方法。由于平均分配法没有考虑各指标对综合评价的贡献差异；专家评判存在一定的主观性，可能导致权重分配差异较大。如何客观地给出指标权重分配，成为迷彩伪装效果评价中的难题。针对该问题，于金［6］和崔宝生［7］利用BP 神经网络得到了指标权重，但这种方法需要大量的训练样本和专家先验信息；同时文献［3，8-9］中提出了基于熵权法［10］的权重分配方法，但权重计算并未考虑各个指标对整体评价的贡献程度。

本文基于模糊聚类方法［11-14］、结合信息熵与统计特征，设计了一种新的权重分配算法。与BP 神经网络相比，模糊聚类无需提供任何专家先验信息，就能够定量地确定样本的亲疏关系，从而客观地划分样本的类型。因此，从客观的数据集中确定各评价指标的权重分配。最后通过实验验证了本文算法的可行性。

1 伪装效果评价模型

现有的客观评价迷彩伪装效果方法是计算目标背景与迷彩的相似度。本文采用文献［8］的方法，将迷彩伪装场景的结构相似度、纹理相似度、颜色相似度和二阶统计矩特性作为迷彩伪装评价的4 个指标。对这4 个指标进行加权求和后得到迷彩伪装效果评价的综合相似度。伪装评价方法如图1 所示。

图1 迷彩伪装评价方法

2 权重计算

2.1 信息熵

熵是热力学中表示混乱程度的物理量，香农将熵引入计算机科学，用于描述离散信号的不确定性，可以认为信息熵表征信息量的大小。对于离散随机变量X，其信息熵H（X）的定义如式（1）所示。

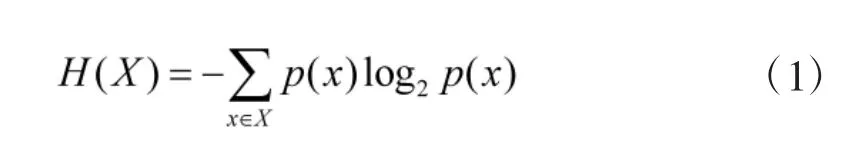
其中，p（x）表示X=x 的概率。

条件熵定义如式（2）所示。

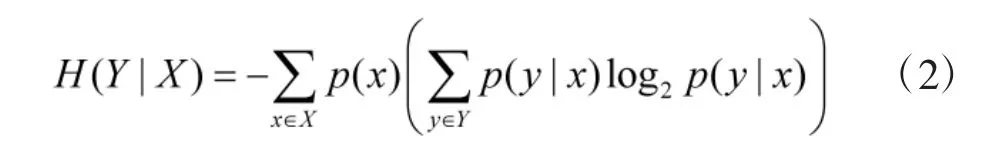
互信息定义如式（3）所示。

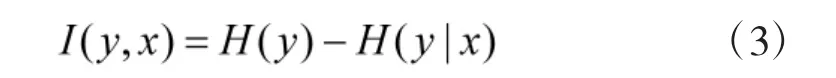
互信息表明X 对Y 贡献的信息量。

2.2 权重分配算法的设计

通过对样本对象的完整指标矩阵和去除某一指标后的非完整指标矩阵进行模糊聚类，并依据其聚类结果计算各指标信息贡献量和重要度，进而计算指标权重。其基本实现流程如图2 所示。

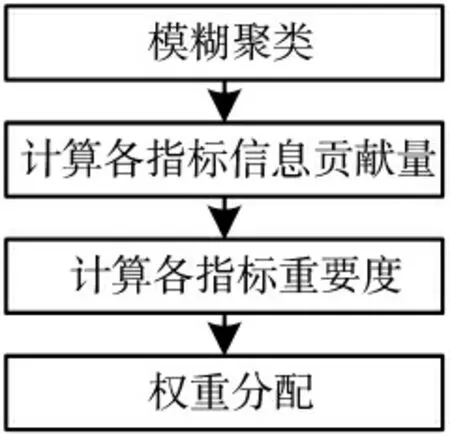
图2 权重分配算法流程

取n 个迷彩伪装样本图像并依据文献［8］的算法进行评价指标计算、整理得到n×4 完整模糊关系矩阵。由于不同指标的量纲和值域不同，需要对该模糊关系矩阵进行归一化处理，并在此基础上运用“最大最小法”［11］构造其模糊关系相似矩阵，通过“平方法”［11］将其改造为等价矩阵，生成并筛选水平截集。依据所得水平截集对样本对象进行聚类［11］，其实现流程如图3（a）所示。

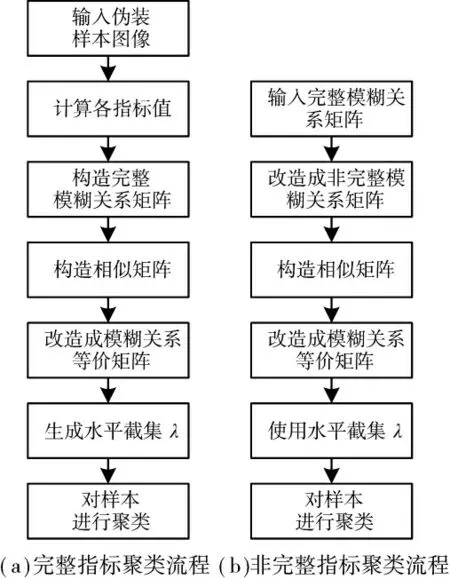
图3 模糊聚类流程

将完整的模糊关系矩阵作为输入，在去除某一指标属性后，再次应用上述过程，并使用完整矩阵的水平截集进行聚类，如图3（b）所示。依次计算并得到结构、纹理、颜色和二阶矩这4 个指标的非完整指标聚类结果。

计算每一个非完整指标聚类结果和完整指标聚类结果的互信息，接着计算并得到各指标对分类结果的信息贡献量，依据指标数值分布的统计特性得到各指标的重要度，并对其进行归一化得到权重分配。

权重计算过程分为4 个步骤，具体描述如下：

步骤1：模糊聚类。

设有n 个样本，每个样本有m 个指标，建立样本对象的指标矩阵X。

由于矩阵X 中各指标的量纲和范围不尽相同，为了避免个别指标对整体效果影响过大，需要对指标进行归一化处理。经过归一化处理后的标准矩阵需要转化为相似矩阵，本文采用“最大最小法”［11］得到相似矩阵R，如式（4）所示。

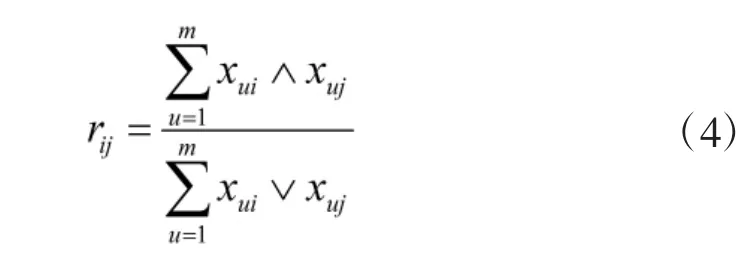
其中，rij表示相似矩阵R 中，i 行j 列的元素。

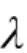
步骤2：计算各属性的信息贡献量。

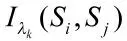
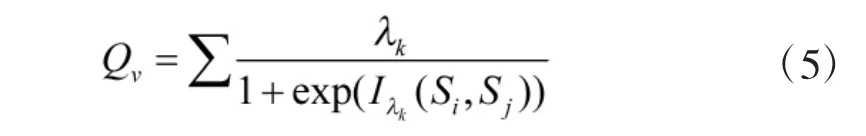
步骤3：计算各属性的重要度。

重新考察归一化之后的模糊关系标准矩阵，发现对于样本的某一属性（即对应于标准矩阵中的某一列），如果其数值分布过于集中，可以认为该指标对评价结果的贡献较小；反之，如果数值分布较为分散，可以认为该指标有利于样本分类［2-3，8-10］。引入标准差来修正互信息量所产生的误差，如式（6）所示。

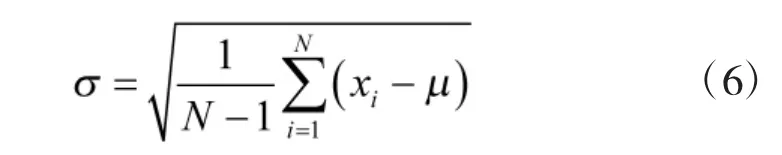
其中，μ 表示均值，N 为样本总数，σ 为标准差。

定义指标的重要度为Mv（v=1，2，…，n），如式（7）所示。

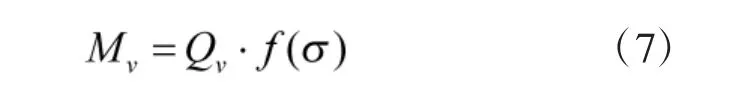
其中，f（σ）是关于σ 的单调增函数。由于各属性的σ 差异较大，特别是倍数差异过大，为了避免σ 对权重施加过大的影响，需要缩小σ 之间的倍数差异。f（σ）的设计需要满足缩小倍数差异的特征。本文取

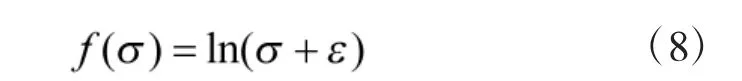
其中，ε 为修正参数。经大量测试后发现，ε=1.2 时修正效果较好。

将式（8）带入式（7）得到式（9）如下：

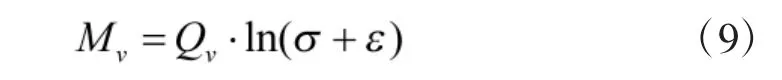
步骤4：获得权重分配，并进行权重计算。

通过对各指标的重要度归一化得到权重分配，如式（10）所示。

其中，v=1，2，…，n。wv表示对应指标的权值。

3 实验设计与验证

针对上述设计的权重分配算法，在文献［8］的基础上，本文选取某地区背景图像进行了实验验证与分析。在下页图4 中，（a）为原始背景图像，（b）、（f）、（h）是采用原始背景主色分别设计的大斑点、数码、自然纹理迷彩；（c）、（g）、（i）是采用常规海洋主色分别设计的3 种迷彩图案；（d）是单色迷彩（绿）；（e）是黑色迷彩（RGB=［30，30，30］）。

图5 为迷彩图案放入原始背景中的效果。在此基础上，依据文献［8］的方法计算伪装效果指标并采用本文方法计算各指标权重。整个实验分为4 个步骤：计算指标值、模糊聚类、计算指标权重、伪装效果评价。

3.1 指标值计算

图4 背景图像及迷彩图案

图5 迷彩图案放入原始背景中的效果

本文采用文献［8］的方法计算并整理得到各迷彩图案的指标数据，如下页表1 所示。由表1 数据可直接建立样本对象的模糊关系矩阵。

由表1 可知：不同迷彩的结构相似度大致接近；数码迷彩、自然纹理迷彩的纹理相似度和二阶统计矩明显高于其他迷彩；从颜色相似度来看，采用常规主色的迷彩颜色相似度都低于0.65，与背景图像的色差较大，而采用背景主色的大斑点、单色、数码、自然纹理迷彩的颜色相似度大部分都高于0.8，与背景的色差较小。

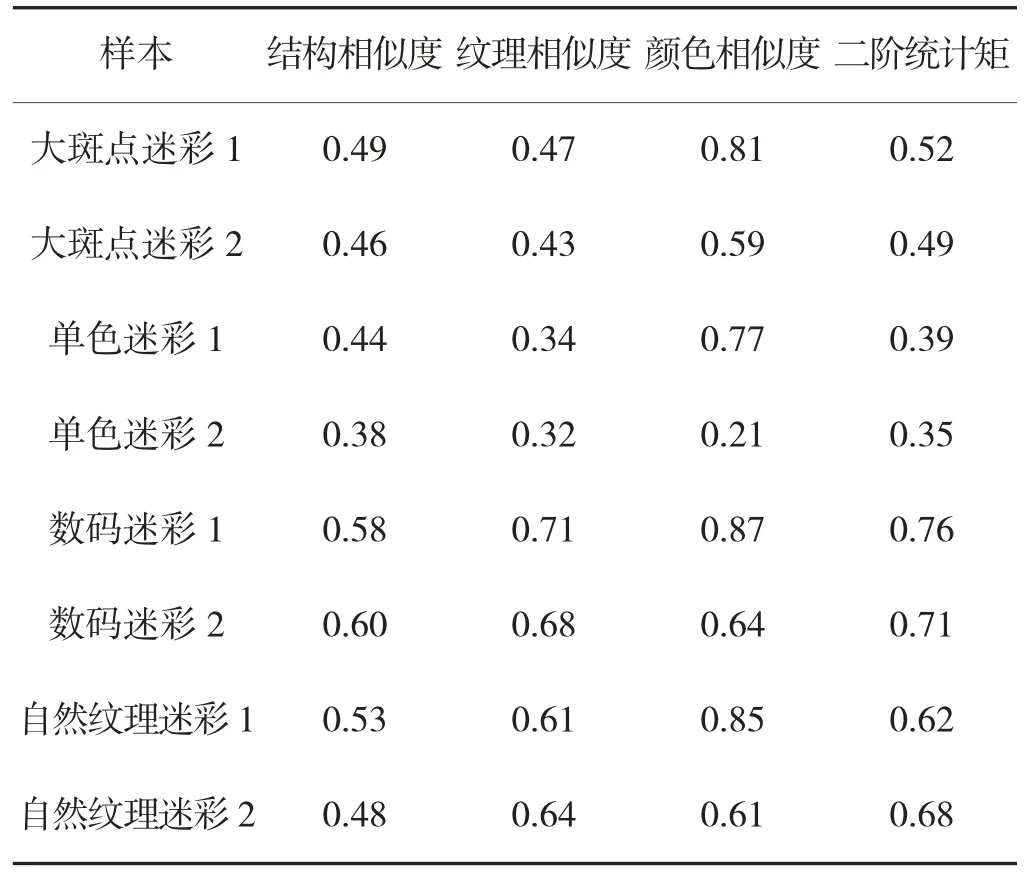
表1 样本指标数据

由于4 个指标的取值都在［0，1］内，该指标矩阵不需要进行归一化处理。采用最大最小方法得到指标矩阵的相似关系矩阵，并通过平方法得到其传递闭包R*，R*即为模糊关系等价矩阵。取R*中排名前4 的非1 数值作为水平截集={0.946，0.902，0.880，0.857}。

3.2 模糊聚类

依据水平截集得到不同截取水平下的聚类结果。如表2 所示，其中，x1至x8代表1 中大斑点迷彩1 至自然纹理迷彩2 样本。

表2 完整指标聚类结果

此时的聚类结果为Si（i=1，2，3，4）。采用同样的方法，计算去除了颜色相似度指标后的模糊关系矩阵，并在水平截集为时得到聚类结果，如表3 所示。

此时的聚类结果为Sj（j=1，2，3，4）。

同理，可分别得到去除结构相似度、去除纹理相似度和去除二阶统计矩之后的聚类结果。

3.3 计算指标权重

依次去除某一指标属性后，再次对新的模糊关系矩阵进行模糊聚类，可得到多个分类结果。运用式（1）～式（3）计算聚类结果之间的互信息，然后将其结果代入式（5）得到各指标的信息贡献量，最后计算各指标的标准差σ，运用式（9）（取ε=1.2）计算得到每个指标的重要度，归一化结果，从而得到各指标的权重分配。

表3 去除颜色相似度之后的聚类结果

经上述过程得到的权重分配，与采用专家评判法、熵权法计算所得结果的对比，如表4 所示。

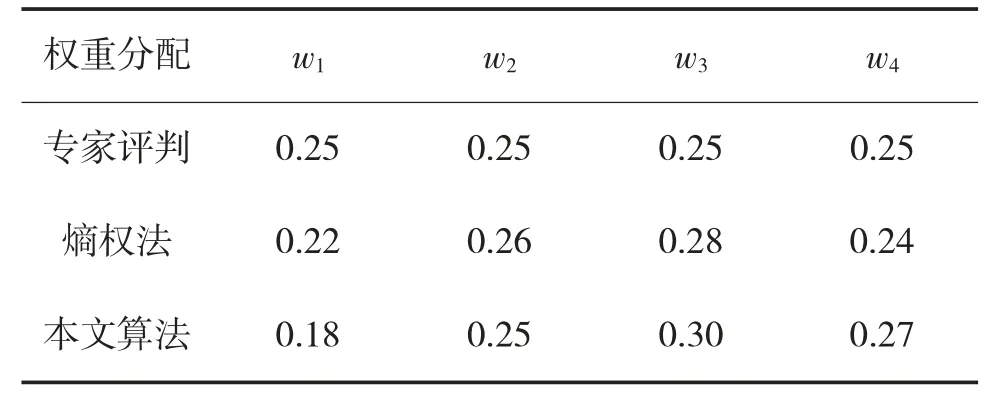
表4 权重分配结果比较

其中，w1、w2、w3、w4分别为结构相似度、纹理相似度、颜色相似度和二阶统计矩的权重值。

由表4 可知：专家评判采用平均分配原则，不能体现各指标对伪装效果的贡献度；熵权法没有考虑各指标对整体评价的贡献程度，存在局限性；本文算法通过引入指标贡献度和标准差，提高了指标权重分配的精度，较前两者更为客观准确。

3.4 伪装效果评价

将表4 中的权重应用于表1 中的相似度数据得到综合相似度，如下页表5 所示。

由表5 可知：专家评判法、熵权法和本文算法都能描述样本的实际伪装效果，但是数码迷彩2 和背景的色差过大，比自然纹理1 更为显著，然而专家评判法的结果表明自然纹理1 的伪装效果要弱于数码迷彩2，与事实相悖。同时，大斑点2 和背景的色差较大，相比之下单色1 与背景的差异更小，但是专家评判法和熵权法都不能提供有效的评价，而本文算法的结果与事实相符，能够更好地描述各伪装效果评价指标之间的关系，较其他算法更为优秀。

4 结论

本文基于模糊聚类方法、结合信息熵和统计特性建立了迷彩伪装效果评价的多指标权重分配模型。相比传统的权重分配方法，本文算法同时考虑了指标的贡献程度和指标自身的分布特征，提高了权重的精度。选取了某地区图像进行了迷彩伪装效果评价实验，并依据实验结果分析了专家评判法和熵权法中存在的问题。实验结果表明，采用本文算法可以有效利用样本数据所包含的信息对指标权重进行客观地分配，提高了评价结果的科学性和准确性。

表5 综合相似度