基于改进稀疏线性预测的时延估计算法
贺 良, 郭海燕, 何宏森, 王学渊
(西南科技大学 信息工程学院,四川 绵阳 621010)
0 引 言
阵列麦克风信号的时延估计(TDE)是许多声源定位算法的第一步,也是语音增强的第一步,在室内声学环境声源定位和讲话者跟踪识别中起着重要作用。广义互相关(GCC)[1]是迄今为止应用最为广泛的TDE技术,该方法依赖于信号的频谱特性,通过最大化互相关函数得到的时延值作为时延估计值。然而,当混响或噪声很强时,可以发现GCC的TDE性能显著恶化。由于接收信号的频谱特性是通过房间中的多径传播来修改的,因此,可以通过强调与频率相关的权重来使GCC功能更加稳健。基于这种思想,相位变换广义互相关(GCC-PHAT)[2]通过PHAT加权使幅度谱严格预白化,在一定程度上提高了TDE对噪声和混响的鲁棒性。
就预白化而言,线性预测作为一项重要的技术已经应用于TDE算法[3]。传统线性预测器的配置,采用长期预测器和短期预测器级联的方式来实现,得到的预测系数向量非常稀疏[4]。然而,当语音信号被噪声污染时,这种稀疏性降低甚至不存在,因而导致线性预测器的性能降低。针对这一问题,一种可行的方案是,将线性预测器系数向量的稀疏性用于构造L2/L1范数优化模型,进而预白化用于时间延迟估计的麦克风信号;结果表明,L2/L1-LP预白化的TDE算法对于噪声和混响的免疫性得到有效提高[5]。
基于稀疏性约束的原理,本文提出一种基于改进L2/L1范数线性预测(improved L2/L1-norm linear prediction,Im-L2/L1-LP)预白化的时延估计器。
1 Im-L2/L1-LP预白化的TDE
1.1 优化模型
假设在远场有一个宽带声源辐射平面波,利用麦克风阵列来拾取声音信号。这里采用线性预测器预滤波麦克风信号,为此,可以利用通道过去的样本来预测其当前样本[5],即
x(n)=X(n)a+e(n)
(1)
式中 误差信号向量e(n)可用于定义最小化的代价函数,解这个函数就能找到预测器系数向量a的最佳估计。在文献[5]中,利用系数向量的稀疏性构造L2/L1-LP预白化的时延迟估计器,获得了对噪声的鲁棒性。然而,在反射主导环境中,这种稀疏性减弱甚至消失,导致预测器对麦克风信号的白化能力变弱。
众所周知,纯净语音信号的短时傅立叶变换(STFT)的幅度谱|FX(n)|是稀疏的。经验观察表明,在混响主导环境中麦克风信号的STFT的幅度谱也是稀疏的,如图1(a)所示;并且,麦克风信号的短时变化趋势(反映其低频成分)通常可以预测。因此,预测信号矢量X(n)a的幅度谱|FX(n)a|通常具有稀疏性。为了增强TDE对混响的鲁棒性,在预测信号X(n)a的幅度谱上引入对最小二乘模型的稀疏性约束。为此,提出以下凸约束线性预测模型
(2)
式中 ‖·‖1和‖·‖2分别为L1范数和L2范数,λ1>0和λ2>0为正则化参数。
实验结果表明,语音幅度谱稀疏性的引入增强了预测器的预白化能力(比较图1(c)和图1(b)可以看出)。值得注意的是,当λ2=0时,优化模型(2)与文献[5]模型一致;当λ1=0时,优化模型(2)则退化为Lasso模型。
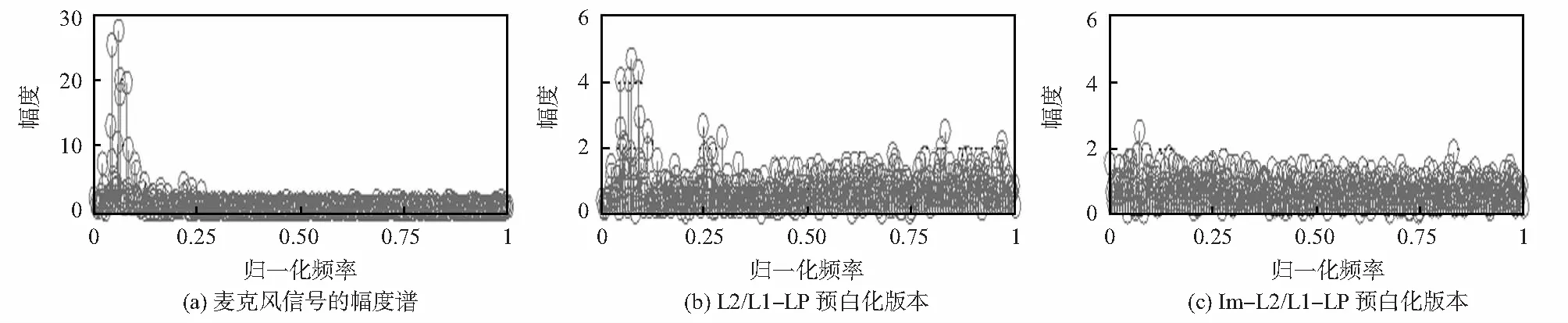
图1 混响主导环境预白化效果对比
1.2 优化模型的解
通过引入辅助向量u和p,采用split-Bregman迭代方法[6]可以获得求解式(2)的迭代算法如下:
初始化:k=0,a0=u0=p0=b0=g0=0
ak+1=[(1+λ)XT(n)X(n)+λI]-1×[XT(n)x(n)+λ(uk-bk)+λXT(n)F-1(pk=gk)]
bk+1=bk+ak+1-uk+1
gk+1=gk+FX(n)ak+1-pk+1
k=k+1
end while
λ>0为惩罚参数,b,g为Bregman向量,F-1为傅立叶矩阵F的逆矩阵。shrink(·)为软函数:shrink(ξ,μ)=sgn(ξ)⊙max{|ξ|-μ,0},∀ξ∈RK+L,μ>0,其中,sgn(·)为符号函数,⊙为点积,K为预测器的长度,L为帧长。
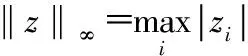
一旦利用Im-L2/L1-LP对麦克风信号实施预白化处理,就可以找到预测误差信号e(n)之间互相关函数(CC)的最大值,从而实现TDE。
2 仿 真
对于前两种算法,预测器长度设置为128。对于所提出的算法,向量a,u,p,b和g的初始状态均为零向量,迭代次数设置为50,δ1= 0.001,δ2= 0.001,惩罚参数λ=1.0。
实验在7 m×6 m×3 m的模拟房间内进行。房间中的位置由三维坐标(x,y,z)来指定,以房间地面的西南角作为坐标原点。两个麦克风间距为0.1 m,分别放置于(1.94,4.00,1.40)和(2.00,4.08,1.40),声源位于(4.09,1.19,1.40)。使用image模型[7]生成从声源到两个麦克风的脉冲响应。通过将语音源信号与生成的脉冲响应进行卷积产生混响语音信号,然后加入零均值高斯白噪声以控制信噪比(SNR),进而获得麦克风输出信号。这里采用均方根误差(RMSE)[8]来评估所提算法的性能。声源信号是来自男女朗读声的语音信号段,采样率48 kHz,信号时长约为2.5 min。在仿真过程中,麦克风信号被分成互不重叠的帧,测试总帧数为1 000帧,帧长128 ms,真实时延为4.0个样本间隔。仿真结果如图2所示。
图2(a)描绘了轻度混响环境(T60=200 ms)时延估计的均方根误差与信噪比的关系。从图中可以看出,在噪声主导(例如,SNR< 10dB)的环境中,L2/L1-LP算法比GCC-PHAT获得更好的噪声鲁棒性;随着信噪比提高,在混响主导(例如,SNR>20 dB)的环境中, GCC-PHAT由于具有对混响更好的免疫能力,反而比L2/L1-LP算法获得更好的鲁棒性。从图中还可以看出,无论是在噪声主导还是在混响主导的环境,所提出的Im-L2/L1-LP算法性能相比于L2/L1-LP算法都较为明显的提高,而且在混响主导的环境中获得了与GCC-PHAT相近且更优的鲁棒性。
图2(b)展示了弱噪声环境(SNR=10 dB)时延估计的均方根误差与混响时间的关系。从图中可以看出,当T60=0 ms时,Im-L2/L1-LP算法获得最佳性能,表明该算法确实对噪声具有鲁棒性,而GCC-PHAT算法对噪声相对敏感。比较两种线性预测算法可以看出,所提算法在噪声主导环境(例如,T60<200 ms)获得了与L2/L1-LP算法相近且更好的性能,而在中度和重度混响混响环境(例如,T60>300 ms)较大程度提高了TDE算法的鲁棒性。
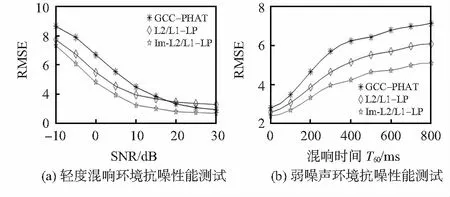
图2 仿真结果
3 结 论
噪声与混响测试实验表明:模型中幅度谱稀疏性约束的引入,使得所提算法在保留并优化L2/L1-LP算法抗噪性能的同时,显著提高了其抗混响能力(尤其是在混响主导环境),在三种预白化的时延估计算法中获得最佳鲁棒性。

