一种改进的蝙蝠算法*
周贤泉, 宋 威, 张士昱, 王晨妮
(江南大学 物联网工程学院,江苏 无锡 214122)
0 引 言
近来,群体智能算法作为一类优化算法越来越为人所知[1~3],2010年Yang X S教授提出了蝙蝠算法(bat algorithm,BA)[4],2011年Yang X S根据蝙蝠算法处理多目标的优化问题,取得了很好的效果[5,6]。在蝙蝠算法的优化过程中,蝙蝠个体通过调整对应的响度与脉冲率,改变自身的位置,并且追随最优的蝙蝠个体,从而找到全局最优解。该算法是搜索全局最优解的有效方法并且收敛较快,但是也存在求解精度不高、易陷入局部最优的缺陷。文献[7]针对蝙蝠算法求解精度不高进行了相关改进,但是也存在容易陷入局部极值的问题。
本文在文献[7]基础上提出4个方面的改进,并最终通过对UCI中的数据集进行聚类测试,发现提出的改进蝙蝠算法能够有效的解决文献[7]中存在的问题。
1 蝙蝠算法介绍与分析
1.1 蝙蝠算法描述
蝙蝠算法[8]原理:首先初始化每个蝙蝠个体的位置与速度,并且把这些蝙蝠个体所在的位置当做求解问题空间的解,求出每个蝙蝠个体对应的适应度函数值。在迭代过程中,每个蝙蝠个体都会调整对应的脉冲率与响度,向着最优蝙蝠个体所在的位置移动,最终可以寻找到全局最优解。
1.1.1 蝙蝠算法的全局搜索
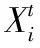
fi=fmin+(fmax-fmin)β,β∈[0,1]
(1)
(2)
(3)
式中β为[0 , 1]之间的一个随机数,fi为第i只蝙蝠当前的频率,X*表示在当前迭代过程中所有蝙蝠个体中最佳个体对应的位置。在求解优化问题中,fi的取值根据问题领域的大小确定,假设fmin=0,fmax=2,那么在蝙蝠算法寻优过程中,每只蝙蝠都从[fmin,fmax]之间随机获得对应的频率。
1.1.2 蝙蝠算法的局部搜索
蝙蝠个体局部寻优时,一旦搜寻到更优解,蝙蝠个体就会在随机游走中就近产生,其局部寻优公式为
Xnew=Xold+εAt
(4)

(5)
(6)
式中α,γ都为常数,对于任意0<α<1和γ>0有
(7)
蝙蝠算法初始化时,每只蝙蝠个体的响度与脉冲率随机设定,一般响度在[1 , 2]之间,脉冲率一般在[0 , 1]之间,在蝙蝠个体寻优过程中,响度与脉冲率是不断更新的。
1.2 蝙蝠算法实现步骤
假设求解目标函数f(x)的极小值,其中,x=[x1,x2,…,xd]T,种群大小为Np,t=1,最大迭代次数为Tmax,响度为A,脉冲率为r,用以下伪代码表示蝙蝠算法求解优化问题的基本步骤:
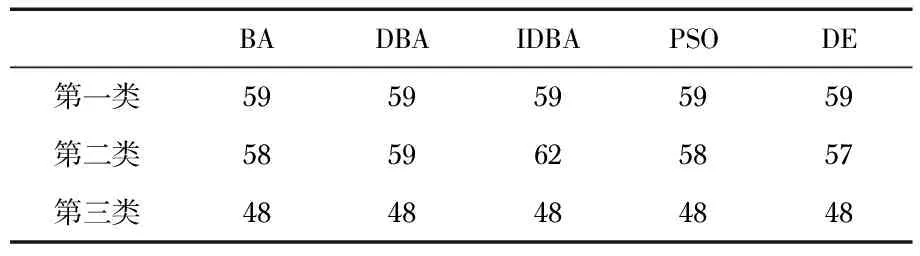
Whilet Fori=1 toNp 根据式(1),式(2),式(3)生成新的解Xnew Ifrand>ri 根据式(4)产生一个局部解Xnew End if ifrand Xi=Xnew fitness(i)=f(Xnew) 根据式(5),式(6)更新Ai和ri End if End for 蝙蝠个体按照对应的适应度值从小到大排序,找到最佳蝙蝠个体,更新X* End While dBA[7]算法由Chakri A于2016提出,本文基于dBA基础上提出一种改进的BA(improved-DBA,IDBA)算法。 2.1.1 IDBA全局寻优策略 在求解优化问题时,往往存在多个极值,如果像文献[7]中蝙蝠群体朝着最佳的蝙蝠个体位置移动,那么蝙蝠个体不仅容易陷入局部极值,而且会使得种群多样性急剧减少,所以,本文首先将蝙蝠个体按照对应适应度值从小到大排列,保存其中适应度值较低的一些个体,然后在全局寻优过程中,蝙蝠个体随机从适应度值较低的个体中选择一个个体指导蝙蝠个体寻优,这样避免蝙蝠个体朝着单个最佳蝙蝠个体位置移动,以防止蝙蝠个体陷入局部极值。 蝙蝠个体在迭代过程中存在个体历史最优位置,这些位置周围也可能存在全局最优解,所以,本文借鉴粒子群算法[2]中的寻优策略,在蝙蝠个体全局寻优策略中向着此个体迭代过程中的历史最佳位置前进以促进蝙蝠个体寻优。 蝙蝠发出的脉冲可以沿不同的方向发射,蝙蝠两只耳朵可以接受回波,假设每只蝙蝠可以发射2个可能是有用的脉冲到2个方向,所以,提出两种全局寻优策略 (8) (9) (10) 2.1.2 IDBA指引方向 式(10)中的全局寻优策略Xnew1示例图如图1(a)所示,表示出在Xnew1对应的全局寻优策略中,加上指引方向gdirection相比于不加指引方向离全局最优解位置更近。 如图1(b)可知,如果每次能够得到较好的指引方向,那么就能够在较少的迭代次数内寻得全局最优解。 图1 蝙蝠全局寻优策略 2.1.3 IDBA局部寻优策略 提出的IDBA算法引用文献[7]中的局部寻优策略 (11) (12) 式中w0=(Ubi-Lbi)/4,w∞=w0/4。 2.1.4 IDBA响度和脉冲率更新 2010年,Yang提出蝙蝠个体在迭代过程中根据式(5)和式(6)来更新响度和脉冲率,以此方法快速的搜寻到最优解。脉冲率决定蝙蝠个体是否进行局部寻优,如果脉冲率在较少的迭代次数内变得很大,那么如1.2节原始蝙蝠算法所示,蝙蝠个体就会有较低的概率进行局部寻优;同样,如果响度A的值在较少的迭代次数内变得很小,根据1.2节蝙蝠算法中可以看出这样不利于全局寻优得到的更优解。 本文引用文献[7]中脉冲率与响度的变化策略。脉冲率随着迭代次数的增加而缓慢的变大,响度随着迭代次数的增加而缓慢的变小。早期较小的脉冲率与较大的响度使得蝙蝠个体在全局搜索的过程中也能有很大的概率进行局部寻优;后期虽然脉冲率较大,但是也存在一定的概率进行局部搜索,响度虽然较小,同样存在一定的概率进行解的更新,所以,设定IDBA算法中的脉冲率与响度如式(13),式(14)所示变化 (13) (14) 2.1.5 IDBA优胜劣汰策略 在IDBA算法中,每只蝙蝠个体在迭代后对蝙蝠个体按照适应度值从小到大进行排序,并且随机初始化蝙蝠个体总数的30 %的新个体代替适应度值较大的蝙蝠个体。这样增加蝙蝠个体的种群多样性,增强所有蝙蝠个体的全局寻优能力。 假设某数据集X存在m类样本,对数据集X进行聚类。将各中心点与对应样本的余弦距离和作为求解的适应值函数。 Step 2 Whilet Fori=1 toNp IfGVi=Φ,设定GVi=零向量,否则从矩阵 GVi中随机选择一个向量作为gdirection, 根据式(8)、式(9)、式(10)生成新的解Xnew End if Ifrand>ri 产生一个局部解Xnew End if ifrand GVi←Xnew-Xi IfGVi方向数超过Np,随机删除一些方向向量, 使GVi向中方向个数不大于Np End if fitness(i)=f(Xnew) End if End if End if Step 3 设定参数C,算法每迭代C次设定GVi=Φ。 Step 4 优胜劣汰策略,对蝙蝠个体按照适应度值从小 到大排序。然后初始化一些蝙蝠个体,个体数 为蝙蝠个体总数的30 %,并且代替适应度值较 小的30 %个蝙蝠个体 End End While 蝙蝠个体按照适应度值从小到大排序,找到最佳蝙蝠个体x*,可视化聚类结果 本文选择UCI(http;//archive.ics.uci.edu/ml/)中的3个数据集作为各对比实验的聚类测试数据集。数据集1选择Iris数据集,包含150个样本,每个样本包含4个属性,分为3类,每类有50个样本。数据集2选择Wine数据集,包括了3种酒中13种不同成分的数量,数据集每行代表一种酒的样本,共有178个样本,其中,第1类有59个样本,第2类有71个样本,第3类有48个样本;数据集3选择Sonar数据集,包括了2类样本,每类样本有60个属性,第一类有97个样本,第二类有个样本101个样本。 为了避免各维度取值范围不一致对聚类测试产生影响[9],实验前采用极大值标准化对各数据集进行归一化处理 (15) 式中i为数据集中的样本个数,j为样本维数。 准确率(precision,P)[10]是指聚类正确的样本与该类原有样本数量之间的比值 (16) 式中Mi为第i类中的样本数量,mi为正确聚类到第i类中的样本数量,P越大说明聚类效果越好。 本文选择余弦相似度[11]对相似的样本进行归类,通过计算2个向量的夹角余弦值来评估相似度 (17) 式中a与b分别为两个样本,cosθ越小说明两个样本之间相似性较低,cosθ越大说明两个样本之间相似性较高,两个样本可以归为一类。 本实验硬件环境:PC(CPU∶2.53 GHz,内存∶2 GB),软件环境Windows 7操作系统,在MATLAB R2014a编译器上实现。 4.5.1 实验结果 分别根据BA,DBA,IDBA,PSO,DE算法对数据集1、数据集2、数据集3进行聚类测试。对每个算法独立运行 30次,最好的每类聚类正确的样本个数如表1、表2、表3所示。 表1 各算法对应的数据集1聚类正确的样本个数 表2 各算法对应的数据集2聚类正确的样本个数 表3 各算法对应的数据集3聚类正确的样本个数 图3为数据集1、数据集2、数据集3对应的各智能算法运行30次得到的聚类准确率。 图3 三个数据集对应不同算法的聚类准确率 4.5.2 实验分析 由图3(a)可知,对于数据集1,原始BA,PSO,DE算法容易陷入局部极值使得聚类准确率较低只有66.67 %。文献[7]中的改进BA算法虽然能够得到比较稳定的聚类结果,但精度不是很高,本文算法,不仅能够得到比较稳定的聚类结果,而且测试精度达到98 %。由图3(b)可知,对于数据集2,本文提出的改进的蝙蝠算法IDBA相比于其他智能算法,聚类结果更稳定并且能够得到更好的聚类准确率94.4 %。由图3(c)可知,对于数据集3,本文提出的改进的蝙蝠算法IDBA相比于其他智能算法,虽然聚类结果同样不是很稳定,但聚类准确率最高,准确率为69.23 %。 本文提出的IDBA算法相比于文中涉及到的其他智能算法收敛性更稳定,鲁棒性更强,并且求解精度较高,但该算法存在设置的参数较多的问题,参数设置不当可能得不到更好的解,接下来该研究合适的参数,使得对于大部分优化问题都可行。2 改进的蝙蝠算法
2.1 Improved-dBA算法
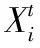
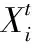
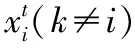


3 IDBA算法聚类应用实现步骤
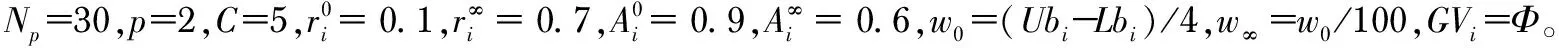
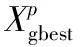
4 实验与结果分析
4.1 数据集
4.2 聚类评价指标
4.3 聚类准则
4.4 实验参数设置

4.5 聚类测试结果与分析



5 结 论

