微细特征三维测量系统标定的精确椭圆提取方法*

何万涛, 王 磊, 郭延艳, 孟祥丽

(1.岭南师范学院 机电工程学院，广东 湛江 524048； 2.岭南师范学院 信息工程学院，广东 湛江 524048)

0 引 言

随着精密制造技术和计算机技术的发展，工业和生活中很多产品都在向小型化和轻便化的方向发展，很多工业领域的产品体积变得越来越小。因此，在产品制造和加工过程中出现了大量针对微细特征零件的检测任务，如零件的形状和尺寸公差检测、表面质量和缺陷检测等。然而，传统的人工方法(目测、样板)等方法存在着效率低、精度差和劳动强度大等多种问题。随着计算机和图像处理技术的快速发展，基于视觉的三维测量系统在零件三维测量中得到了广泛应用[1]。孔玮琦等人[2]利用远心镜头高分标率和畸变非常小的特点，开发了小微物体光学三维测量系统，并提出了一种基于一般模型的系统参数标定方法。陈超等人[3]通过将体视显微镜、相机和投影仪进行组合来适应不同大小零件的精密测量，研制了基于正弦光栅条纹投影的三维小视场成像系统。彭翔等人[4]通过引入通用的成像模型，在充分利用有限景深的情况下，开发了专用的标定程序，实现了小微零件完整的三维重建。

上述小微三维测量系统在硬件和软件开发方面都进行了卓有成效的研究，并根据小微物体的特点和系统的景深等特性建立了通用的模型，提出了与系统相适应的标定方法[5]。系统参数标定是微细特征三维测量系统的核心，直接决定着小微物体的测量精度[6]。然而，系统参数标定精度一方面取决于成像模型，另一方面取决于系统的图像输入。在建立精确的成像模型的同时，需要高精度地提取标定用图像的圆心、角点等特征信息进行输入，当同时具备2个条件的情况下才能标定获取到高精度的系统参数。

椭圆是模式识别和机器视觉中一个非常重要的基元。因此，已经开发了各种椭圆提取算法。霍夫变换和最小二乘是两种常用的方法，霍夫变换算法对离群值不敏感，可以同时检测多个基元。然而，该算法存在阈值选择、峰值查找、存储容量大、精度低等问题。其他算法，如最小二乘法涉及迭代拟合，并将数据点与估计弧之间的误差最小化。虽然计算速度快、精度高，但对异常值非常敏感，通常会导致非最佳结果，甚至失败，计算稳定性差。

本文针对现有算法存在的问题，提出了一种鲁棒、快速、有效的椭圆提取算法。利用Zernike矩检测椭圆的边缘，基于矩阵的块分解提出了一种改进的拟合方法。

1 亚像素边缘检测与椭圆拟合

Zernike矩[7]是用于模式识别和机器视觉等的重要数字图像描述子。Teague首先介绍了使用Zernike矩来克服流行几何矩中存在的信息冗余的缺点。Zernike矩是一类正交矩，在图像表示方面表现出了很好的效果。矩是旋转不变量，可以很容易地构造成任意顺序。Zernike矩多项式是一组定义在单位圆上复杂的正交多项式，其n阶多项式定义如下

Vnm(ρ,θ)=Rnm(ρ)ejmθ

(1)

多项式Rnm可以表示成如下形式

Rnm(ρ)=

(2)

N阶的Zernike矩定义如下

(3)

当f(x,y)为离散函数时，Zernike矩为(x,y)和Vnm(ρ,θ)的卷积，可表示为

(4)

式中f(x,y)为图形的灰度分布，并且x2+y2≤1。

7×7的模板单位圆如图1所示，图中的每个正方形像素的大小可以根据式(3)计算得到。图2是亚像素边缘检测的理想模型。

在单位圆中L为理想边缘，h和h+k为灰度分布，l为中心点o和线L之间的距离，φ为旋转角。

这里Zernike矩的0～4阶结果为

(5)

边缘检测的步骤如下：

1)根据式(5)计算Zernike矩Anm；

2)根据式(5)计算l1,l2,h,k和φ

(6)

式中 Im[A31]和Re[A31]为A31旋转前的虚部和实部。

3)考虑到n×n掩模的放大，用边缘检测公式计算边缘

(7)

式中l=(l1+l2/2)。

通过上述计算获得图像特征亚像素边缘后，采用文献[8]中的矩阵分块法对椭圆进行拟合与中心计算。

2 标定流程

在计算得到准确的椭圆中心坐标后，采用经典的张正友[9]平面标定法进行相机的内外参数标定。系统的标定流程如图3所示。其中,相机拍摄的图像应该尽量覆盖每个相机的整个测量空间。完成每个相机的标定后，利用左右相机同时拍摄一组标定板在不同位置的图像，以尽量覆盖双相机的视场为准。

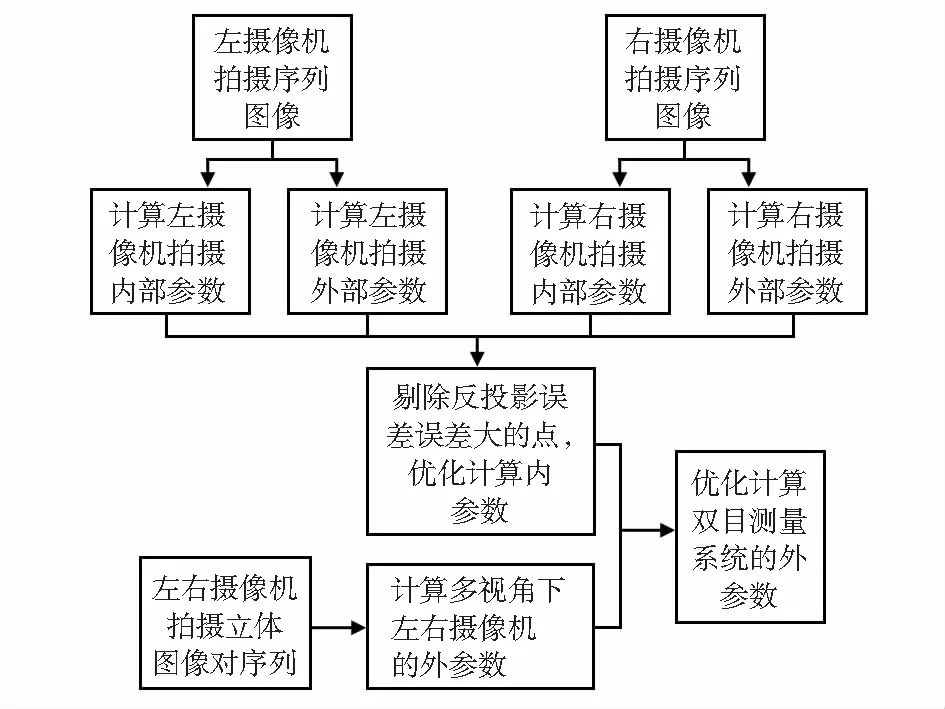
图3 标定计算流程图

3 实验与结果分析

3.1 实验参数设置

基于双目的微细特征三维测量实验系统如图4(a)所示，系统的硬件包括：2台德国Basler的230万像素的usb3.0工业相机，1台DLP微型的蓝光投影机，带有背光源的小型标定板。其中，相机的CMOS靶面尺寸为1/1.2 in(l in=2.54 cm)；像元尺寸为5.86 μm×5.86 μm；分辨率为1 920像素×1 200像素。配备日本的computar的百万像素25mm焦距的工业相机镜头。蓝光DLP投影的分标率为1 200像素×720像素，亮度150流明。标定板上带有不同大小圆点的11行×9列的99个圆点，点与点之间的距离是3 mm，如图4(b)所示。

3.2 椭圆拟合与标定实验

在标定实验前，首先进行了椭圆拟合实验，首先，对模拟图像进行边缘检测与中心提取，并与传统的Sobel算子进行了比较。模拟图像通过画图软件绘制4个标定板上的大圆。考虑到实际的COMS传感器和光学系统对图像的平滑作用，对生成的图像经邻域平滑后进行提取与计算，验证算法的精度，仿真实验图像及边缘检测结果如图4(c)所示。

图4 实验系统与标定

由表1不难看出，本文算法提取的图像圆心更加接近图像的理想值，偏差在0.05像素左右，这种精度完全可以胜任微细特征测量系统的精度要求。

在实际的提取实验中，对标定板在三种不同的曝光时间下进行图像采集，如图5所示，然后进行椭圆拟合与中心提取，提取结果如图6所示，进而验证算法的鲁棒性。

图5 三种不同曝光的标定板图像

图6 不同曝光标定板椭圆拟合结果

从图6中不难看出，其中的(a)和(b)中的圆心提取全部正确，共计提取出35个圆心。而(c)中虽然35个圆心提取正确，但在图像的左上角出现了部分错误的圆心，这主要是由于图像的过度曝光导致相机的电子噪声过大引起的。其中的正确圆心用圆点表示。通过仿真与实际实验，验证了所提出的椭圆拟合算法的精度与稳定性。

3.3 三维重构与分析

为了进一步证明本文提出的椭圆拟合算法的精度与稳定性，对标定过程中拍摄的标定板图像分别进行了三维重建，并与标定板制造厂商给定的标准值进行了比较。其中的位置1的标定板三维重建的点云如图7(a)所示，5个标定位置的重建结果如图7(b)所示，结果分析如表2所示，这其中只对标定板上4个大点之间的水平和垂直距离(如图4(b)所示)进行了比较与分析。标定板上的1-4两个大点之间的距离标准值为12.002 4 mm；2-3点之间的距离为18.002 7 mm(标定板出厂时采用高精度影像测量仪测得的值)。

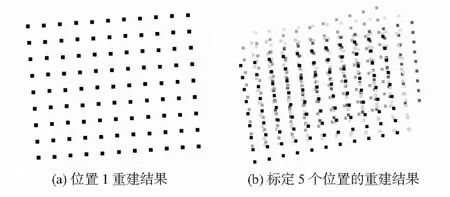
图7 三维重建结果

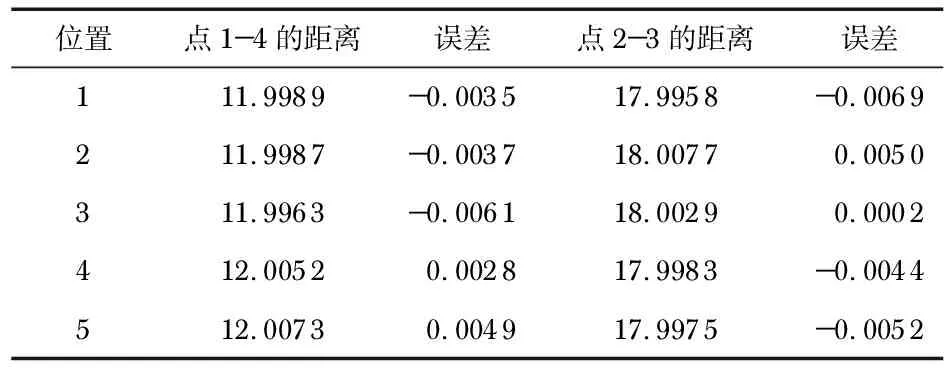
位置点1-4的距离误差点2-3的距离误差111.9989-0.003517.9958-0.0069211.9987-0.003718.00770.0050311.9963-0.006118.00290.0002412.00520.002817.9983-0.0044512.00730.004917.9975-0.0052

表2中的标定板的1-4大点之间的距离，也就是垂直距离的最大值为12.007 3 mm，最小值为11.996 3 mm，最大测量误差为-0.006 1 mm；标定板的2-3大点之间的距离，也就是水平距离的最大值为18.007 7 mm，最小值为17.995 8 mm，最大测量误差为-0.006 9 mm。由表2可以看出，以重建标定板的三维点最大误差作为评价标定精度，该系统的标定重建精度可以达到7 μm。

4 结 论

在微细特征的物体测量系统中，图像边缘的提取精度对系统的标定和测量精度影响更加敏感，为此提出了一种基于Zernike矩的边缘检测算法。通过对不同曝光图像进行圆心提取，验证了所提出的算法边缘检测精度高，稳定性好，可为系统标定提供了良好的数据输入。进一步，通过不同空间位置的标定板进行三维重建，并与标定板上圆心点的标准值进行比较，系统的测量精度达到了7 μm，证实了本文方法的有效性。