初中数学几何证明题的解题技巧刍议
周雪梅
摘 要:在初中数学学科中,几何证明题作为一项基础性的题目,是学生学习中的重点问题和难点问题,在初中数学教学课堂中,为了使学生可以具备较为完善的几何证明题解题思路和解题方法,教师一定要向学生更多的讲述一些几何证明题的解题技巧,使学生可以对自身的解题思路进行不断的反思和思考,提高学生的学习效率。
关键词:初中数学;几何证明题;解题技巧
在初中数学几何证明题中,学生在解题的过程中有助于养成较为完善的逻辑思维能力,并且几何证明题可以反映出学生的数学素养以及数学思维,因此在当前初中数学教育课堂中,几何证明题的教学是非常重要的,教师应当从学生当前的学习需求和学习特征出发来对学生进行几何证明题技巧的教学,使每个学生可以掌握相应的几何证明题解题技巧,有效地提高学生解题的正确率。
一、初中几何证明题基本思路
为了有效地提高学生解答几何证明题的正确率,教师要在课堂教学中先向学生明确几何证明题的解题思路,使每个学生可以按照正确的解题方向来进行几何证明题的解答,从整体上看初中几何证明题基本思路主要包括以下几个方面:
(一)审题
在解答初中几何证明题时审题是非常重要的,它不仅可以让学生明确题目中已给的条件,也可以让学生明确题目中各个条件之间的关系,因此教师要要求学生在进行几何证明题解答的过程中一定要全面的审题,学生在拿到一道题目之后,一定要弄懂题目的要求、条件和作用,这样才可以保证学生可以有序的开展后续的解题[1]。教师要要求学生在审题的过程中将已给的条件清晰地标出,对于一些容易犯错误的地方学生要值得注意。例如对于题目:“已知A、B、C三点在同一直线上,AB=10,AC=8,P和Q分别是AB、AC的中点,求PQ的长。”学生在审题的过程中,会有一部分学生审题不认真,误认为C在AB上,这就造成了学生在后续解题的过程中经常会出现一些失误,因此教师在初中数学教学课堂中向学生讲述几何证明题解题技巧时,一定要让学生全面而认真的进行审题。
(二)标注
在对几何证明题进行审题的过程中,标注也是非常重要的,教师要要求学生在审题时一定要弄清题目的题设和结论,并且要将题目中已知条件在图形中进行标记这一步操作是非常重要的,教师在日常教学的过程中一定要向学生进行反复的强调[2]。例如在初中数学中,对于直角或者是等边等角关系的证明题,直接在图形上进行符号的标记,可以让学生一目了然的明白题目中所给的条件。教师要要求学生在标记完成之后,要根据自身的数学基础来进行题目的解答,这样一来每个学生都会形成较为完善而清晰的解题思路,学生的解题正确率也会得到大幅度的提高。
(三)引申
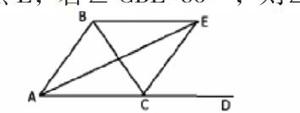
在初中阶段的几何证明题中,有一部分的题型难度是比较大的,并且许多条件都隐藏在题目中,需要学生根据自身的数学基础来进行解答,对于这种题目在解题的过程中需要学生学会引申,就是从所给的条件引申到所需的条件中,从而完成整个证明过程[3]。在解答这一类题型时,不仅要让学生掌握基本的知识点,并且学生还要有一定的空间想象能力,教师要要求学生在审题的过程中要做好标注,并且要让学生思考从这些隐藏条件中可以想到哪些结论,在学生思考完成之后,要在图中进行标注。例如对于下图中的题目:如图△ABC的外角,∠BCD角平分线CE与∠BAC角平分线AE交于点E,若∠CBE=80°,则∠ACE=
对于这道题目的解答,难度是比较大的,大部分学生在解答的过程中经常会出现诸多的问题,这时教师要对学生的解题思路进行全面的引导,教师可以让学生以E为△ABC的旁心,并且运用:三角形一内角与一外角的角平分线的交点,其夹角等于第三个内角的一半的理论。教师要让学生在解答的过程中运用这一定理来进行解答,当学生运用这一定义进行解答时会发现整个问题是非常简单的,学生遇到难题也会迎刃而解。
二、解题思路的总结
(一)基本图形
在初中幾何题中,基本图形的题型主要是为了反映概念和定理,这是学生进行初中几何证明题解答的基础步骤,在利用基本图形进行解答时,可以帮助学生从一些复杂的图形中找出解题思路,另外也可以帮助学生更快的发现添加辅助线的方法,因此教师在初中数学教学课堂中在向学生进行几何证明题教学时,应当善于引导学生从一些复杂的图形中分解出基本的图形,并且要让学生从已学的理论出发来进行实地的操作,之后,再由学生的实践上升到更高层次的解答,从而使学生形成较为完善的解题思路。
(二)辅助线
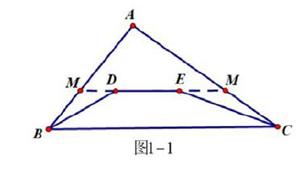
辅助线是学生在解答初中几何证明题时必备的一项解题思路,辅助线的添加是几何证明题的难点,因此教师应当在初中数学教学课堂中对学生进行几何证明题教学时,应当对学生进行辅助线的教学,使每个学生可以掌握更多的画辅助线的技巧,教师要告诉学生在画辅助线时应当遵循化繁为简的基本原则,通过辅助线的添加可以把一些不规则的图形转换为规则图形,在画辅助线时通常用于一些求图面积的题型,例如最为常见的辅助线划分方法是连接四边形的对角线或者是平移对角线,辅助线是沟通命题中已知和求证结论的桥梁,因此掌握正确添加辅助线的方法是非常重要的。例如对于这道题:已知如图1-1:D、E为△ABC内两点,求证:AB+AC>BD+DE+CE.
学生在解答时可以按照这两种思路来进行解题:证明:(法一)将DE两边延长分别交AB、AC 于M、N,
在△AMN中,AM+AN > MD+DE+NE;(1)
在△BDM中,MB+MD>BD; (2)
在△CEN中,CN+NE>CE; (3)
由(1)+(2)+(3)得:
AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CE
∴AB+AC>BD+DE+EC
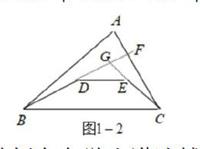
或者是通过这种方法来进行解答:如图1-2, 延长BD交 AC于F,延长CE交BF于G,
在△ABF和△GFC和△GDE中有:
AB+AF> BD+DG+GF (三角形两边之和大于第三边)(1)
GF+FC>GE+CE(同上)………(2)
DG+GE>DE(同上)……………(3)
由(1)+(2)+(3)得:
AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE
∴AB+AC>BD+DE+EC。
教师在向学生讲述辅助线的做法时,应当根据一个题目来为学生进行有效的扩展,教师要要求学生在画辅助线时,应当仔细的观察题目中的要求,并且要运用自身的分析能力来转化题干中的内容,结合重要的知识点来进行问题的转化,创设由已知条件向所求结论的过渡,使得一些复杂的几何问题得以解决。值得注意的是教师要告诉学生在画辅助线时,并不是简单的在平面图形上乱贴乱画,而是需要学生提前根据题目中所给的内容和要求来进行条件的创造,从而可以快速的得出问题的结论,教师要鼓励学生在进行几何证明题解答的过程中,应当根据自身的数学基础来对辅助线的添加进行大胆的设想。
结束语
在初中数学教学课堂中,教师一定要向学生讲述一些几何证明题的解题思路和解题技巧,使每个学生的空间想象能力和逻辑思维能力可以得到有效地提高,教师应当让学生从图形的规律和各种题型的解题思路出发,将一些未知的条件转换为已知的结论,从而最大程度的提高学生解题的正确率。
参考文献
[1]何晓明.初中生几何证明题解题错误的解决对策[J].数理化解题研究,2017(11):21-25.
[2]朱毅刚.初中数学几何证明的解题思维培养路径探析[J].理科考试研究,2016(6):26-30.
[3]葛敏洁.初中数学几何证明题思路探析[J].数学教学通讯,2018(5):120-123.

