腹板开孔冷弯槽钢梁直接强度法研究
赵金友,高 攀,孙 阔,王 钧
(东北林业大学 土木工程学院,哈尔滨 150040)
近年来,随着各国冶金技术的发展,冷弯型钢构件的板厚变得更薄,在荷载作用下更易发生屈曲破坏,这使得冷弯型钢构件的稳定承载力成为了研究焦点[1]。早期,各国规范主要采用有效截面法作为冷弯型钢构件的承载力设计方法,但该方法的计算过程相对繁琐且仅适用于发生局部屈曲的构件[2],因此,一种新的承载力设计方法——直接强度法(DSM)应运而生。DSM由美国学者Schafer和Peköz于1998年首次提出,该方法无需逐个计算截面中各个板件的有效宽度,而是将整个截面作为一个整体来考虑,计算过程相对简单,且考虑了构件发生畸变屈曲和局部-整体相关屈曲两种情况[3]。
为方便水管、电线以及暖气管道在梁、柱和墙等构件中通过,常在冷弯型钢构件的腹板中预先开设孔洞,孔洞的出现势必会对构件稳定承载力产生影响[4]。美国学者MOEN[5]基于腹板开孔冷弯槽钢梁的屈曲性能试验成果,提出了适用于腹板开孔冷弯型钢受弯构件的DSM承载力设计公式,该系列公式已被列入现行北美冷弯型钢结构设计规范(NAS)(2016)的正文[6],但在MOEN的试验研究中仅出现了畸变屈曲起控制作用的屈曲破坏模式,且试件腹板开孔尺寸远大于工业标准化孔洞尺寸(宽101.6 mm、高38.2 mm)[7],可见,现行NAS中腹板开孔冷弯型钢受弯构件的DSM承载力设计公式尚缺乏相关试验数据的有力支撑。
我国最新版《冷弯型钢结构技术规范》(GB 50018-2017)在附录中首次给出了采用DSM来考虑畸变屈曲影响的承载力设计内容,但此次规范的修订仅引入了无孔构件的DSM承载力设计公式,对于开孔构件的DSM承载力设计方法并未有明确条文予以规定[8]。可见,提出适用于腹板开孔冷弯型钢受弯构件承载力设计的DSM计算公式是我国目前亟待解决的问题。
1 直接强度法(DSM)承载力设计公式简介
美国学者Schafer和Peköz基于17名研究者的574组无孔受弯构件的试验数据,经回归整理得到了适用于无孔冷弯型钢受弯构件的承载力设计方法——DSM[3]。该方法先后于2004年和2005年被北美和澳大利亚冷弯型钢结构设计规范引入[9-10]。其原始计算公式分别考虑了畸变屈曲和局部-整体相关屈曲两种屈曲破坏模式。
无孔冷弯型钢受弯构件发生畸变屈曲破坏时受弯承载力为:
(1)
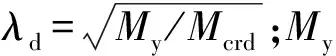
无孔冷弯型钢受弯构件发生局部-整体相关屈曲破坏时受弯承载力为:
(2)
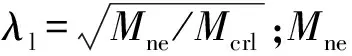
2016年,NAS(2016)在正文中给出了腹板开孔冷弯型钢受弯构件的DSM承载力设计公式,公式中通过引入净截面边缘屈服弯矩Mynet来考虑开孔对构件受弯承载力的影响,即当净截面边缘屈服弯矩与毛截面边缘屈服弯矩的比值Mynet/My=1时,该设计公式与无孔构件的DSM承载力设计公式无异[6]。其原始计算公式同样考虑了畸变屈曲和局部-整体相关屈曲两种屈曲破坏模式。
腹板开孔冷弯型钢受弯构件发生畸变屈曲破坏时受弯承载力为:

(3)
式中:Mynet为净截面边缘屈服弯矩;
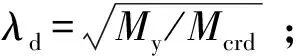
Mcrd为考虑孔洞影响的弹性畸变屈曲临界弯矩(Mcrd=fcrdWf,其中fcrd为考虑孔洞影响的弹性畸变屈曲临界应力,Wf为截面模量);My为毛截面边缘屈服弯矩。
腹板开孔冷弯型钢受弯构件发生局部-整体相关屈曲破坏时受弯承载力为:
(4)
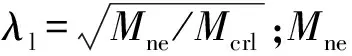
2 已有试验及有限元参数分析简介
腹板开孔冷弯槽钢梁的试验数据及有限元参数分析数据分别来源于文献[11]和[12].文献中梁长度L均为3 720 mm,跨中1 200 mm区段为纯弯研究区段,腹板孔洞均开设在梁的研究区段,开孔形式包括不同孔高比(孔洞高度与腹板高度的比值)的矩形孔洞和不同孔高比(孔洞直径与腹板高度的比值)的圆形孔洞。梁截面形式及几何参数定义如图1所示。文献[11]和[12]中梁的开孔形式及截面几何参数列于表1,试验和有限元参数分析共计360组。试验加载装置如图2(a)所示, 试验时,两个完全相同的试件在加载处与支座处分别通过荷载连接件和支座连接件背靠背连接在一起,连接方式分别如图2(b)和2(c)所示。试验加载现场及有限元参数分析模型分别如图3和图4所示。有限元模拟试验所得试件受弯承载力与试验结果最大偏差仅为6.8%,因此采用本文中有限元模型对腹板开孔冷弯槽钢梁开展大量参数分析是可行可靠的。

图1 梁截面形式及几何参数定义Fig.1 Types and geometric parameters of beam section

表1 试验试件及有限元参数分析构件统计Table 1 Statistics of specimens and FEA members
试验及有限元参数分析中卷边长度为20 mm的开孔梁均发生了以畸变屈曲为主的破坏模式,而卷边长度为40 mm的开孔梁均发生了以局部屈曲为主的破坏模式,典型的屈曲破坏模式分别如图5和图6所示。相比于无孔冷弯槽钢梁,腹板开孔冷弯槽钢梁的受弯承载力有不同程度的降低,且降低幅度随孔高比的增大而增大。所有开孔梁的受弯承载力和屈曲破坏模式不予一一列出,详见文献[11]和[12].
3 开孔冷弯槽钢梁弹性屈曲临界应力求解方法
弹性屈曲临界应力的求解是运用DSM预测腹板开孔冷弯槽钢梁受弯承载力的关键环节。虽然采用有限元程序中特征值屈曲分析可准确地求得腹板开孔冷弯槽钢梁的弹性屈曲临界应力,但由于建立有限元模型的复杂性,该方法很难在工程设计中得以应用和推广。目前,有限条法(如:CUFSM有限条程序[13])是求解冷弯型钢构件弹性屈曲临界应力行之有效的方法,但对于存在截面突变的腹板开孔冷弯槽钢梁,该方法无法直接应用[14]。

图3 试验加载现场Fig.3 Overall view of loading rig

图4 有限元参数分析模型Fig.4 Finite element parameter analysis model
文献[11]和[12]中,基于ANSYS有限元程序求得的腹板开孔冷弯槽钢梁弹性屈曲临界应力,验证了基于折减腹板厚度法采用有限条程序CUFSM求解此类构件弹性畸变屈曲临界应力的准确性,并对已有此类构件的弹性局部屈曲临界应力近似计算公式进行了修正。

图5 开有不同孔高比矩形孔洞的试验梁Fig.5 Test beams with rectangular holes with different ratios of hole height-to-web depth

图6 开有不同孔高比圆形孔洞的有限元分析梁Fig.6 FEA beams with circular holes with different ratios of hole height-to-web depth
3.1 弹性畸变屈曲临界应力建议求解方法
腹板开孔冷弯槽钢梁弹性畸变屈曲临界应力可由式(5)配合CUFSM有限条程序求得[5,15]。
fcrd=min(fcrdg,fcrdn) .
(5)
式中:fcrdg为不考虑孔洞影响的梁弹性畸变屈曲临界应力,可由无孔梁的有限条分析得到,如图7所示;fcrdn为考虑孔洞影响的梁弹性畸变屈曲临界应力,可由折减截面的有限条分析得到,截面折减如图8所示,图中折减截面的腹板厚度t由折减厚度tr代替,具体的腹板折减计算公式为[15]
(6)
式中:tr为考虑孔洞影响的腹板折减厚度;t为原始截面厚度;Lh为孔洞总宽度(腹板矩形开孔时Lh=N·b;腹板圆形开孔时Lh=N·be,其中be为等效孔洞宽度,即采用等面积、等高度的原则,将圆形孔洞转化为矩形孔洞,具体计算公式为be=πd/4);Lcrd为畸变屈曲半波长,可由无孔梁的有限条分析得到,如图7所示。

图7 无孔梁CUFSM有限条程序分析结果Fig.7 Analytical results of Finite strip program of beams with no holes

图8 截面修正Fig.8 Modified section
3.2 弹性局部屈曲临界应力建议求解方法
文献[11]和[12]中,通过引入了与孔高比及截面形式有关的系数对MOEN et al[15]给出的腹板开孔冷弯槽钢梁弹性局部屈曲临界应力fcrl的近似计算公式进行了修正,应用修正后的该系列公式得到了较为准确的弹性局部屈曲临界应力预测结果。腹板开孔冷弯槽钢梁弹性局部屈曲临界应力可由式(7)求得[11-12]。
(7)
式中:fcr为腹板上无孔洞影响的有支撑板件的弹性局部屈曲临界应力;fcrh为腹板上邻近孔洞的单侧无支撑板件的弹性局部屈曲临界应力。fcr可由式(8),(9)和(10)求得。
(8)
k=2(1+ψ)3+2(1+ψ)+4 .
(9)
(10)
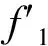
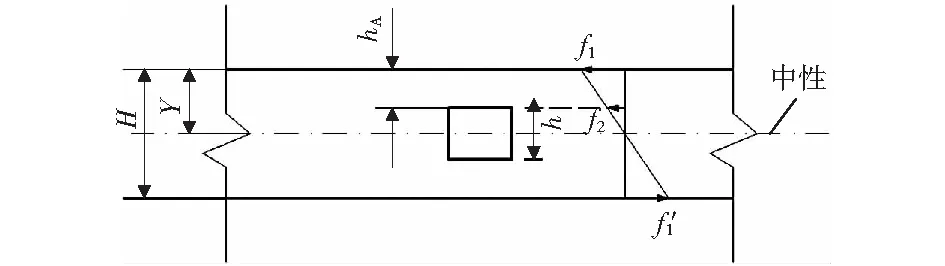
图9 弹性局部屈曲临界应力近似计算公式中参数示意Fig.9 Illustration of parameters in approximate critical elastic local buckling stress Equation
fcrh可由式(11),(12),(13)和(14)求得。
(11)
(12)
(13)
(14)
式中:hA代表腹板孔洞的位置(见图9);fcrA为孔洞至少有一部分位于受压区时(即hA 如图10和图11所示,令开孔梁受弯承载力Mu与毛截面边缘屈服弯矩My的比值Mu/My为纵轴,λd=(My/Mcrd)0.5或λl=(My/Mcrl)0.5为横轴,绘制NAS(2016)中腹板开孔冷弯型钢受弯构件DSM公式(式(3)和式(4))曲线,并对360组试验及有限元参数分析所得数据进行了处理,绘制成图10和图11中散点,与公式曲线进行对比。对比时,根据净截面边缘屈服弯矩Mynet与毛截面边缘屈服弯矩My比值φ=Mynet/My的不同进行分类。将构件值满足φ∈(0.975,1)的数据点与φ=1的DSM公式曲线进行对比,构件值满足φ∈(0.925,0.975)的数据点与φ=0.95的DSM公式曲线进行对比,构件值满足φ∈(0.875,0.925)的数据点与φ=0.90的DSM公式曲线进行对比,以此类推,已有试验及有限元参数分析数据共涉及φ=1,φ=0.95和φ=0.85三类。 图11 局部屈曲起控制作用的开孔梁DSM原始与修正曲线散点对比图Fig.11 Comparison of original and modified scatters for beams with web holes controlled by local buckling 由图可见,绝大多数散点位于DSM公式曲线的下方,其中,发生以局部屈曲为主破坏的开孔梁的散点与DSM公式曲线的偏差尤为显著,即采用NAS(2016)中腹板开孔冷弯型钢受弯构件DSM承载力设计公式预测此类开孔梁的受弯承载力是偏于不安全的。因此,对原始公式(式(3)和式(4))中的系数、指数及分界点进行了调整,得到了适用于腹板开孔冷弯槽钢梁承载力设计的DSM修正公式(式(15)和式(16)),修正公式曲线如图10和图11所示。从图中可以看出,全部散点均分布在修正公式曲线的附近,经统计,由DSM修正公式预测所得畸变屈曲起控制作用和局部屈曲起控制作用的腹板开孔冷弯槽钢梁受弯承载力与试验及有限元参数分析所得梁受弯承载力比值的平均值分别为1.06和1.01,相应的标准差分别为0.06和0.04,绝大多数预测结果误差不超过10%,公式修正效果较为理想。 腹板开孔冷弯槽钢梁发生以畸变屈曲为主破坏时受弯承载力为: 腹板开孔冷弯槽钢梁发生以局部屈曲为主破坏时受弯承载力为: (16) 将已有的360组腹板开孔冷弯槽钢梁的试验结果及有限元参数分析结果与现行北美冷弯型钢结构设计规范(NAS)(2016)中腹板开孔冷弯型钢受弯构件DSM承载力设计公式曲线进行了对比,由对比可知:对于绝大多数腹板开孔冷弯槽钢梁而言,NAS(2016)中DSM的承载力预测结果是偏于不安全的,其中对于发生以局部屈曲为主破坏的开孔梁的预测结果偏差尤为显著。因此,基于已有的试验结果、有限元参数分析结果和弹性屈曲临界应力求解方法,给出了适用于腹板开孔冷弯槽钢梁承载力设计的DSM修正公式。4 腹板开孔冷弯槽钢梁DSM修正公式的建立


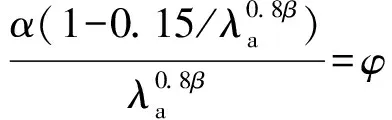
5 结论

