轻钢屋面系统精细化设计方法研究

李元齐，周皓雪，栾 蔚，郑 瑜，黄 林

(同济大学 a.土木工程学院，b.土木工程防灾国家重点实验室，上海 200092)

轻钢屋面系统由于自重轻、强度高、施工方便、防水密闭性能好等众多优点被广泛应用于工业与民用建筑，同时由于其重量轻、相对薄柔，风荷载成为其设计的重要荷载之一。因此，基于风荷载的传力路径，针对屋面系统各构件的风致破坏模式，系统地研究关键构件的有效风荷载及其精细化设计理论与方法，有利于实现轻钢屋面系统在我国安全、经济的应用。

典型的轻钢屋面系统是由冷弯薄壁檩条、压型钢板、连接紧固件及拉条等共同组成的檩条覆板体系。轻钢檩条作为轻钢屋面系统中的重要构件，其抗扭性能和在弱轴方向的抗弯性能较差，受弯时易发生弯扭失稳[1-3]。而屋面系统可以为檩条提供一定程度的侧向支撑和扭转约束作用，在设计中恰当考虑可显著提高檩条的稳定承载性能，降低屋面系统的用钢量[4]。

根据屋面板之间以及屋面板与檩条的连接构造方式，可分为锁螺钉屋面系统、暗扣屋面系统和直立锁缝咬合屋面系统三大类[5-7]。其中国内外关于锁螺钉屋面系统中檩条承载性能的研究较多，CHU et al[7-9]针对受金属屋面部分约束的C、Z形檩条建立了分析其弯扭屈曲性能的简化模型，并采用能量法求解檩条临界荷载研究其影响因素，结果表明，侧向约束通常可以提高檩条的弯扭屈曲临界荷载，提高程度与边界条件、荷载位置及是否设置拉条等因素有关，翘曲应力仅当构件的边界为固定并且没有拉条时对弯扭屈曲有显著影响；张耀春等[10-11]采用3种经典的有限元模型，考虑檩条腹板高厚比、翼缘宽厚比、檩条侧向长细比以及蒙皮对檩条扭转约束刚度的影响，对风吸力下Z形檩条的弯扭屈曲临界荷载开展参数分析，提出了风吸力作用下考虑蒙皮支撑作用的Z形檩条临界荷载简化计算公式，与我国门式刚架规程的计算结果对比表明该简化算法高效准确。

关于目前普遍使用的直立锁缝屋面系统，CARBALLO[12]针对重力荷载作用下Z形檩条支承的直立锁缝屋面系统，开发了4种预测破坏荷载的方法，建议采用“Base Test Method”的方法确定重力荷载作用下直立锁缝屋面系统中Z形檩条的承载力，该方法经过ANDERSON[13]修正之后应用于风吸力作用工况下，之后被北美规范[14]采纳，本文采用该方法开展足尺试验，分析檩条破坏形式及影响檩条承载力的因素。童根树等[15-16]参照欧洲规范建议的标准试验方法开展试验，并通过有限元模型对比分析，证明体系的总扭转刚度由屋面板、可滑动支架和檩条三者的扭转刚度串联而成。上述研究表明，通过标准构件试验方法可以较为准确地获得屋面系统对檩条的扭转刚度，但连接刚度的具体计算方法仍有待进一步研究。

现行规范[17-18]中只考虑了屋面板与檩条牢固连接时屋面系统对檩条的约束作用，对于其他连接形式，未作详细规定，或仅简单规定不考虑屋面板的约束效应，不能满足该类结构体系合理设计的要求，导致设计普遍浪费或存在安全隐患。因此，针对轻钢屋面系统的典型构造特点，系统地研究檩条覆板屋面系统中屋面板对檩条扭转和侧移约束作用的精确量化技术，是实现各类轻钢檩条精细化设计的关键科学问题之一。

1 轻钢屋面系统风荷载研究

1.1 轻钢屋面风荷载风洞试验研究

在结构抗风设计中，建筑物表面风压分布特性是分析结构风荷载的基础。双坡屋面刚性模型测压试验在同济大学土木工程防灾国家重点实验室TJ-2风洞(2010)和日本东京工艺大学风工程研究中心大型边界层风洞(2018)中分别完成(以下用年份来区分试验)。

试验模型尺寸列于表1，比例系数列于表2.《门式刚架轻型房屋钢结构技术规范》GB 51022-2015[19]在考虑风荷载时，将屋面划分为角部、边区和中间区，两次试验均在三个区域选取了典型的测点，部分试验模型见图1.

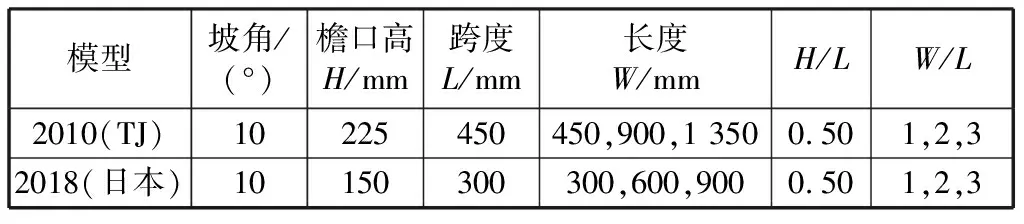
表1 试验模型尺寸Table 1 Geometry parameters of models

表2 试验比例系数Table 2 Similar ratios in tests

图1 试验模型布置Fig.1 Set-up of test models

1.2 试验结果

考虑到结构的对称性，图2和图3仅给出工况1中M1模型在0°、45°和90°风向角下测得的平均风压系数和脉动风压系数，其中指向屋面板的方向为正。

图2 平均风压系数Fig.2 Mean wind pressure coefficients

图3 脉动风压系数Fig.3 Fluctuating wind pressure coefficients

由图2和3可知，两次试验风压系数分布规律大致相同。对于平均风压系数，0°风向角下，整个屋面承受负压，气流在迎风纵墙上翼缘与屋面连接处和屋脊处发生流动分离，在一定范围内形成“分离泡”，产生较大负压，绝对值沿风向方向逐渐减小。45°风向角下，整个屋面承受负压，气流在屋面迎风前缘分离，屋面角部形成极小面积的分离区域，分离区域两侧屋面上形成一对“锥形涡”，靠近屋面角部锥形涡尖端处承受较大负压，沿风向方向负压绝对值逐渐减小。90°风向角下，整个屋面承受负压且关于屋脊对称分布，气流在山墙上缘与屋面连接处发生流动分离，在一定范围内形成“分离泡”，使整个屋面前缘出现较大负压，其绝对值沿风向方向逐渐减小。

对于脉动风压系数，0°风向角下，迎风屋面边缘区域和屋脊处存在较大的脉动风压系数。45°风向角下，脉动风压系数呈锥形分布且不均匀。90°风向角下，迎风屋面角部存在较大的脉动风压系数。

2 屋面板对轻钢檩条实际约束效应

2.1 屋面对檩条的实际约束刚度试验

2.1.1试验概况

对Z、C形冷弯薄壁型钢檩条和两类广泛使用的LSⅢ型和SS360型直立锁缝屋面系统开展足尺试验，两种直立锁缝屋面板分别通过LS003型和S3PC-1型可滑动支架与檩条相连。根据檩条的截面形式和檩条与屋面板的连接方式，考虑拉条设置数量、檩条腹板高度、翼缘宽度及截面厚度等因素，设计以下3个系列试件：a) Z形檩条与屋面板采用可滑动支架连接；b) C形檩条与屋面板采用可滑动支架连接；c) Z、C形檩条与屋面板采用自攻螺钉连接。参照AISI提供的基本试验方法[20]开展屋面-檩条系统足尺试验，由气囊和鼓风机模拟风吸力。

试验在试件檩条的关键研究部位均布置了位移计和应变片，获得檩条的荷载位移曲线，并通过监测竖向及侧向位移辅助判别檩条的破坏模式；同时在试验过程中监测屈曲或屈服发生的时间，并在分析试验数据时辅助确定檩条承载力。

2.1.2试验结果

结果表明，各组试验中间檩条受荷最大，先于其他檩条或屋面组件破坏，拉条的设置状况对檩条的变形特征及破坏模式产生很大影响。图4至图5选取各试验系列中典型试件结果进行说明。

由图4可以看出，对于试验系列1，加载初期檩条跨中竖向位移和上、下翼缘侧移均随荷载增大而线性增长；随着荷载逐级增加，跨中竖向位移和下翼缘侧移进一步增大，在荷载较大时加速增长，呈明显非线性增长趋势，而上翼缘侧移仍基本呈线性增长或增速放缓；临近破坏荷载时，上翼缘侧移明显增大，呈现非线性增长趋势。未设置拉条的试件，加载初期，LSⅢ型屋面系统中的檩条跨中竖向位移和上、下翼缘侧移非常接近，主要产生了竖向和侧向弯曲变形，随后跨中竖向位移和下翼缘侧移始终接近，且远大于上翼缘侧移，扭转变形逐渐增大；SS360型屋面系统中檩条上、下翼缘侧移始终有所差别且小于跨中竖向位移，加载前期主要为竖向弯曲变形，伴有轻微扭转变形，临近破坏时檩条扭转变形逐渐增大。图4(c)、(d)表明在跨中设置拉条后试件中间2根檩条跨中位移基本一致，受力较均匀。三分点各设1道拉条的试件，由于拉条的约束作用下翼缘侧移始终远小于竖向位移，上翼缘侧移在加载初期略大于下翼缘侧移，随着荷载增加逐渐小于下翼缘侧移，临近破坏时上翼缘侧移明显小于下翼缘侧移，截面发生扭转变形。

图4 试验系列1中Z203×64×22×2.2型檩条荷载-位移曲线Fig.4 Load-displacement curves of Z203×64×22×2.2 purlin in test Group 1

由图5可以看出，对于试验系列2，未设置拉条的试件，加载初期檩条跨中竖向位移和下翼缘侧移随荷载增加而线性增大，上翼缘侧移很小；荷载较大时，三者均呈现明显非线性增长趋势，但上翼缘侧移远小于竖向位移和下翼缘侧移。C形檩条在加载初期发生竖向弯曲变形，同时还产生了扭转，随后竖向弯曲变形和扭转变形逐渐增大，还产生了一定程度的侧向弯曲变形。图5(b)、(c)表明设置了拉条的试件檩条跨中竖向位移较侧向位移增长快很多，上、下翼缘侧移随荷载基本呈线性增长，其值较小且方向相反，在荷载作用下檩条发生竖向弯曲变形同时产生了一定侧向弯曲和扭转变形；三分点各设1道拉条的试件，在荷载较大时檩条下翼缘侧移呈非线性增长，临近破坏时扭转变形较为明显。

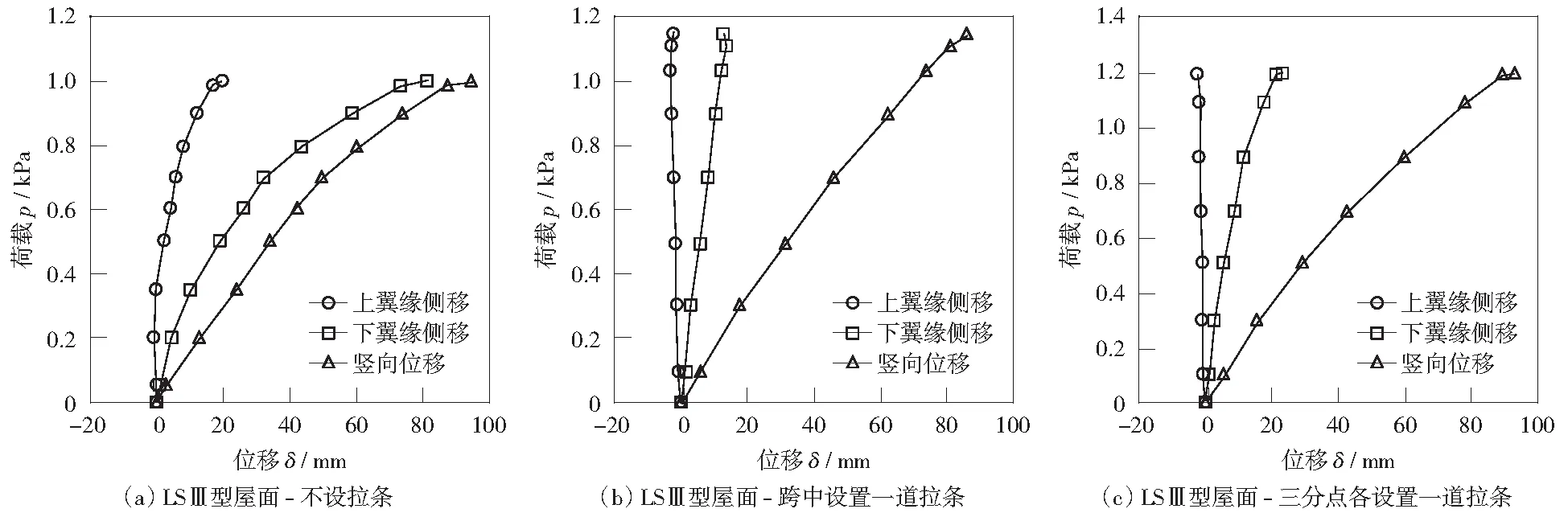
图5 试验系列2中C203×65×21.3×2.0型檩条荷载-位移曲线Fig.5 Load-displacement curves of C203×65×21.3×2.0 purlin in test Group2

试验系列3中檩条与屋面板采用自攻螺钉连接，作为对比试验表明，变形特征与试验系列1，2中同截面类型檩条类似。对檩条Z203×65×22×2.2，由图6可知，LSⅢ型屋面系统中檩条的侧移较大，SS360型屋面系统中檩条的侧移相对较小，采用自攻螺钉连接屋面板与檩条的锁螺钉屋面系统时，加载中前期檩条侧移较小，直至临近破坏时才迅速增大，且最终侧移值也远小于采用直立锁缝屋面情形。

图6 不同屋面系统中Z203×64×22×2.2檩条侧移比较Fig.6 Deflection comparison of Z203×64×22×2.2 purlin among different roof systems

测点对应位置如图7.图8至图9给出了试件中率先发生破坏的檩条跨中截面下翼缘的荷载-应变曲线，横坐标为各测点沿檩条纵向(轴线方向)的正应变。应变受拉为正，受压为负。

试验系列1中除设置1道拉条的试件外，檩条跨中下翼缘各测点的荷载-应变曲线形状都很接近。1，2号应变片位于下翼缘和卷边的交线两侧，加载初期均为压应变，随荷载逐渐增大，达到峰值并反向，未设置拉条的试件中压应变峰值较小，临近峰值荷载时变为拉应变。3号应变片位于檩条下翼缘中部，加载过程中始终为压应变，且基本随荷载增加而线性增大，整个过程中应变值变化较小。4，5号应变片位于下翼缘和腹板的交线两侧，在加载过程中始终为压应变且比其他测点应变大，加载初期随荷载线性增大，之后增速加大呈现非线性趋势，临近破坏荷载时，应变多已达到或超过屈服应变。

图7 测点应变片布置Fig.7 Arrangement of strain gauges

从试件的应变变化情况可以看出，未设置拉条的试件，加载初期主要为竖向向上弯曲，同时存在一定的侧向弯曲变形(采用LSⅢ型屋面系统的试件)或扭转变形(采用SS360型屋面系统的试件)，因而靠近腹板区域压应变较大；加载中后期，檩条竖向弯曲增大的同时还产生了较大的扭转变形，导致靠近腹板区域压应变进一步增大，靠近卷边区域压应变逐渐减小；临近破坏时，檩条跨中竖向和侧向弯曲变形及扭转变形很大，翼缘卷边交线区域受拉，腹板下翼缘交线区域受压屈服。跨中设1道拉条的试件，檩条跨中变形以竖向弯曲为主，临近破坏时跨中附近局部下翼缘卷边外张，导致檩条发生局部屈曲和畸变屈曲破坏，跨中下翼缘卷边附近局部区域压应力减小甚至变为受拉，因此跨中卷边下翼缘交线区域应变在荷载较大时才出现反向，且压应变所达峰值较大；其余区域始终为压应变，且数值较接近。三分点各设置1道拉条的试件破坏形式与不设拉条的类似，但压应变峰值较大。

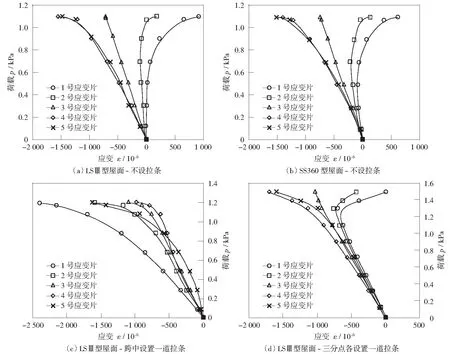
图8 试验系列1中Z203×64×22×2.2型檩条荷载-应变曲线Fig.8 Load-strain curves of Z203×64×22×2.2 purlin in test Group 1

图9 试验系列2中C203×65×21.3×2.0型檩条荷载-应变曲线Fig.9 Load-strain curves of C203×65×21.3×2.0 purlin in test Group 2

试验系列2中，檩条跨中下翼缘各测点应变变化总体趋势与试验系列1较为相似。未设置拉条的试件，C形檩条跨中发生竖向弯曲变形的同时还发生了扭转变形，破坏形式与试验系列1中Z形檩条类似，但三分点各设置1道拉条的试件1，2号应变片压应变峰值较大且临近破坏时仍为压应变。

试验系列3，作为对比试验，总体上檩条的变形特征与试验系列1，2的结果对应。

试验结果表明，试件中拉条设置状况、檩条截面形式以及所采用屋面系统类型不同时，荷载-应变曲线均存在一定差异，结合前述对试验现象和荷载-位移曲线及荷载-应变曲线的综合分析可知，位移、应变数据均与檩条总体变形特征吻合较好。

2.2 屋面对檩条的实际约束刚度数值模拟

为全面准确地分析直立锁缝屋面系统中檩条的受力性能和工作机理，建立了与足尺试验对应的精细有限元模型，通过与试验结果对比，验证了计算模型的准确性。基于验证的精细有限元模型，分析屋面系统为檩条提供的扭转约束及侧移约束刚度。

2.2.1扭转约束刚度分析

图10为用于分析直立锁缝屋面系统扭转约束刚度的有限元模型，由3张直立锁缝屋面板、3排可滑动连接支架和2根支座檩条构成，各构件特性与经试验验证的屋面系统精细有限元模型相同。按图11施加集中力形成扭矩，分别用于分析屋面板和连接支架提供扭转约束刚度和屋面板提供的扭转约束刚度，结果如图12.

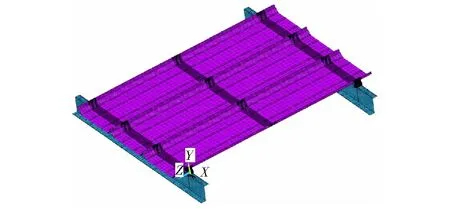
图10 扭转约束刚度分析有限元模型Fig.10 FE model for torsion restraint stiffness analysis

图11 施加集中力形成扭矩Fig.11 Torsion by adding a couple concentrated force

图12 屋面系统和屋面板的扭转约束刚度Fig.12 Torsion restraint stiffness from roof system and roof panel

结果表明，两类直立锁缝屋面系统扭转约束刚度随扭矩变化趋势总体上相似，SS360型屋面系统较早出现下降趋势；给定范围内两类屋面板的扭转刚度基本保持不变，且远大于相应屋面系统提供的扭转约束刚度，LSⅢ型屋面板的扭转刚度略大。综合以上分析，可滑动连接支架时直立锁缝屋面系统中相对薄弱环节，受力过程中产生一定变形，屋面系统对檩条提供的扭转约束刚度不是定值，可用图13所示两折线模型表示，相关参数拟合如表3.该精确模型将用于之后分析屋面系统提供的侧移约束中，以减少误差。考虑到屋面系统中檩条以受弯为主，扭矩较小，为简化分析保守地取与较大扭矩对应的扭转约束刚度值为屋面系统提供的扭转约束刚度，针对研究的两类屋面系统，保守地取60 N·m·m-1对应的刚度3 125 N·m·rad-1·m-1(LSⅢ型屋面系统)和2 947 N·m·rad-1·m-1(SS360型屋面系统)。

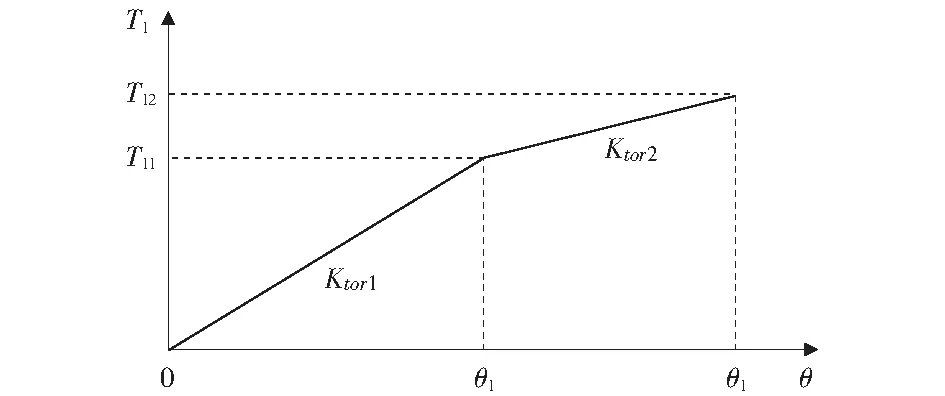
图13 屋面系统扭转约束刚度的精确模型Fig.13 Precise model of torsion restraint stiffness from roof system

对屋面板挠曲变形、支座滑动片与底座相对滑动、屋面板厚度、支架滑动片厚度和支架滑动片宽度5个可能影响屋面系统扭转约束刚度的因素展开参数分析，结果表明屋面板厚度、支架滑动片厚度和支架滑动片宽度对扭转约束刚度产生显著影响，计算时应重点考虑。滑动片厚度变化属于支架类型变化，应另外分析；屋面板厚度影响其自身抗弯刚度和抗扭刚度的同时，对屋面板侧边与支架连接锁缝的刚度有显著影响，进而影响屋面板刚度的传递效率；支架滑动片厚度对连接锁缝处刚度的传递能力也有影响。

表3 两类直立锁缝屋面扭转约束刚度模型相关参数Table 3 Parameters in torsion restraint stiffness model for two types of standing seam roof system

针对屋面板厚度和支架滑动片厚度，对两类直立锁缝屋面系统开展参数分析，归纳得到LSⅢ型屋面系统ktor1和SS360型屋面系统Ktor2为檩条提供的扭转约束刚度的实用简化计算公式：

(1)

(2)

式中：trf为屋面板厚度，mm；ttp为支架滑动片厚度，mm；E为钢材弹性模量，2.06×105MPa.

将上述公式计算结果与有限元计算结果进行对比，对于两类典型屋面系统及连接支架，二者平均误差在5%以内，吻合较好，适用于分析屋面板厚度和支架滑动片厚度在常用范围内时两类屋面系统的扭转约束刚度。

2.2.2侧移约束刚度分析

通过对足尺试验的试验现象和精细有限元模型模拟结果的分析，滑动支架的滑动状况主要分为三个阶段：1) 初始静止阶段；2) 中间滑动阶段；3) 最终静止阶段。因此用三折线模型表示代表屋面系统侧移约束的侧向弹簧刚度进行分析较为准确，将屋面系统对檩条的刚度等效为侧向弹簧和扭转弹簧进行分析，扭转弹簧采用2.2.1中所述两折线模型。

拟合结果表明该简化有限元模型分析得到的檩条破坏模式、荷载-位移曲线和檩条抗弯承载力均与试验结果较相符，但不同试件中两类屋面系统侧向弹簧刚度有一定的离散性，且因开展的足尺试验数量有限，不足以涵盖所有工况，三折线模型在实际应用中过于复杂，因此将侧向弹簧进一步简化为线弹簧，提出两类典型直立锁缝屋面系统侧移约束刚度的实用取值。

Z，C形截面檩条的抗弯承载力随屋面系统侧移约束刚度变化趋势相似，以Z形檩条为例，由图14中典型曲线可以看出，在给定扭转约束作用下檩条的承载力随侧移约束刚度增大而增大，直至侧移约束刚度达到某一门槛值时承载力不再继续增大；侧移约束刚度达到门槛值时檩条的承载力均提升60%左右；屋面系统提供的侧移约束刚度远小于门槛值时，通常可使檩条承载力提高约30%左右。

图14 Z203×64×22×2.2檩条抗弯承载力-屋面侧移约束刚度Fig.14 Bending capacity of Z203×64×22×2.2 purlin to lateral stiffness of roof system

考虑到由试验结果得到的屋面系统侧移约束刚度离散性较大，给定屋面系统扭转约束刚度时，保守地取使承载力提高25%对应的侧移约束刚度作为屋面系统提供的侧移约束刚度。当Z，C形檩条截面高度在160～300 mm，厚度为2～3 mm时，LSⅢ型屋面系统的侧移约束刚度为10 N·mm-1·m-1(Z形截面)和4 N·mm-1·m-1(C形截面)；SS360型屋面系统侧移约束刚度为10.5 N·mm-1·m-1(Z形截面)和4.2 N·mm-1·m-1(C形截面)。对于未设置拉条的檩条，考虑屋面系统扭转约束作用基础上，用该保守值计算得到的檩条承载力普遍低于试验结果，但二者的平均误差仍在10%以内。

2.3 典型屋面系统对檩条约束刚度研究

在对屋面系统整体进行分析之后，针对表4所列四种不同支架连接的屋面系统开展试验，研究屋面系统在风吸力作用下的破坏模式及扭转约束刚度值，并分析屋面系统组件(屋面板、支架、檩条)对扭转约束刚度的影响。试验基于美国钢铁协会AISI标准《梁板组件的侧面转动硬挺度试验方法》(AISI S901-2013)[21]设计，如图15所示(以LS003支架-LSⅢ型屋面板为例)。

表4 试验采用的支架型号Table 4 Types of clips used in tests

图15 试验装置及测点布置(单位：mm)Fig.15 Setup and measuring points in tests(units:mm)

短支架与超级支架的试验现象相似，但破坏模式不同。短支架连接的试件，弹性加载阶段变形主要发生在檩条腹板处，檩条约束翼缘出现局部弯曲变形；之后支架底座开始出现变形，并逐渐与檩条约束翼缘分开，同时檩条腹板与翼缘的变形继续增长；随着荷载增大，屋面板与支架咬合处锁缝变大，支架发生平面外扭转；随着变形的增长，檩条腹板与约束翼缘连接处接触到屋面板；最终由于锁缝持续增大，无法约束支架滑片的平面外变形，支架滑片发生平面外扭转失稳破坏。 超级支架连接的试件，由于支架与屋面板的咬合长度较长，锁缝咬合长度上受到的力相对较小，屋面板锁缝未发生破坏，因此支架没有平面外的扭转失稳，而是支架底座的平面内变形发展较大，且檩条腹板与约束翼缘变形过大，无法继续加载，试件发生破坏。

为研究屋面系统的扭转约束刚度，选取试件破坏的前一级荷载所对应的刚度值作为屋面系统的扭转约束刚度值，此时屋面系统各组件均已经充分变形。图16所示为檩条尺寸相同，不同厚度屋面板及不同型号的支架下屋面系统扭转约束刚度值。

图16 不同屋面板厚度及支架型号下的扭转约束刚度对比Fig.16 Torsion restraint stiffness under different thickness of roof panels and clip types

由图16可以看出，超级支架试件的扭转约束刚度明显比短支架试件大，因为超级支架与屋面板的锁缝咬合长度更大，连接更有效。对于短支架(LS003与LS004)，屋面板的厚度增加，能够有效增加屋面系统的扭转约束刚度；而对于超级支架(LS088与LS089)，屋面板并不是屋面系统中的薄弱环节，因此屋面板厚度的增加对屋面系统的扭转约束刚度并没有明显的影响。超级支架中，低支架(LS088)明显比高支架(LS089)的扭转约束刚度大，因为在加载后期，低支架试件的檩条变形后与屋面板接触，受到屋面板的支撑作用，后期变形减小，刚度退化变小；而短支架在檩条没有发生过大变形时试件已经发生破坏，支架高低对扭转约束刚度没有明显影响。

檩条的变形是屋面系统变形的主要来源，因此檩条是屋面系统扭转约束刚度最重要的组成部分，图17和图18为不同檩条腹板高度与厚度下屋面系统扭转约束刚度对比。可以看出，随着檩条腹板高度增加，扭转约束刚度迅速降低；檩条厚度增加，扭转约束刚度显著增大；对比LS003-2.0与LS088-1.5的曲线及LS003-200与LS088-250的曲线可知，檩条对扭转约束刚度的影响远大于支架的影响。

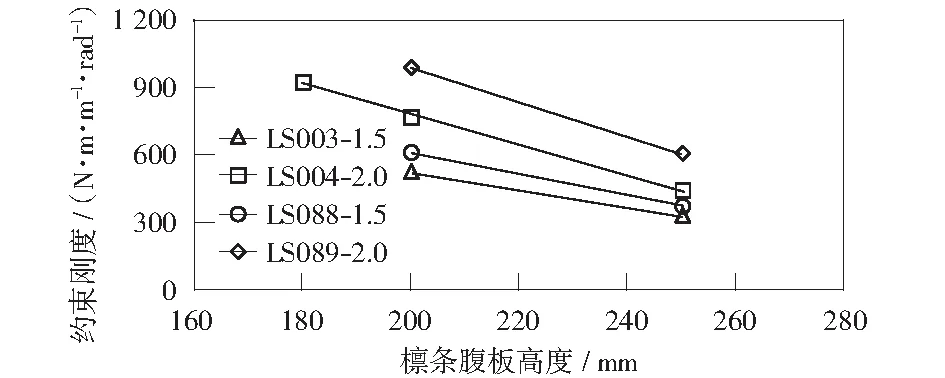
图17 不同檩条腹板高度下的扭转约束刚度对比Fig.17 Torsion restraint stiffness under different web height of purlins

图18 不同檩条厚度下的扭转约束刚度对比Fig.18 Torsion restraint stiffness under different thickness of purlins

针对以上试验，建立有限元模型，从破坏模式、荷载-位移曲线和扭转约束刚度三个方面验证有限元模型的合理性后，结合试验结果对可能影响约束刚度的因素展开参数分析，并归纳得到短支架(LS003与LS004)屋面系统和超级支架(LS088与LS089)屋面系统对檩条约束刚度的计算公式：

(3)

(4)

式中：tlg为檩条腹板高度，mm；tlh为檩条厚度，mm；twm为屋面板厚度，mm；E为钢材弹性模量，2.06×105MPa；λ为支架影响系数，对LS003支架取292，对LS004支架取273，对LS088支架取1033，对LS089支架取988.

将上述公式与有限元分析结果进行对比，发现当屋面系统对檩条的约束刚度过小(Ktor<300 N·m·rad-1·m-1)时出现较大差别，而实际工程中不会使用扭转刚度过小的屋面系统，故其在工程中常用的屋面系统中能够很好地适用。将公式与试验结果进行对比，大部分结果相差10%以内，最大相差17%，较为吻合。

现将屋面系统对檩条约束刚度同2.2.1中给出的实用简化计算公式进行对比。考虑到式(1)给出的是直立锁缝屋面系统屋面板-支架组合对檩条的扭转约束刚度计算公式，而本节还考虑了檩条自身抵抗扭转的作用，为将两者合理对比，在现有有限元模型基础上建立无檩条的屋面系统模型，荷载由支架底座自攻螺钉连接处施加的一对大小相等、方向相反的力模拟，如图19所示。

图19 无檩条屋面系统有限元模型Fig.19 FE model of roof system without purlins

模型采用2.2.1中所用LS系列屋面和对应支架，支架滑片厚度固定，屋面板厚度变化范围为0.50～1.20 mm.将结果与式(1)计算得到的扭转刚度进行对比，结果表明，对不同屋面板厚度，有限元分析所得结果与式(1)计算结果偏差均在10%以内，吻合较好。由此，该分析方法所得的屋面系统对檩条扭转约束刚度能够较好应用到檩条精细化设计中。

2.4 檩条的内力分析

基于试验验证，通过有限元分析和数值积分分析檩条跨度、拉条布置、屋面系统、支座形式等对直立锁缝屋面系统中檩条在弹性阶段内力的影响。

将有限元模型与试验结果进行对比，验证其有效性后，提取各节点应力，通过数值计算得出檩条截面内力沿构件长度方向分布如图20-23.

从有限元分析结果可以看出，拉条的约束对平面内弯矩的分布基本没有影响；平面外弯矩整体与双向受弯构件一致，支架间出现与整体分布趋势相反的局部分布，拉条的约束对平面外弯矩有较大影响；双力矩增长变化呈非线性，受连接支架翘曲约束的影响较大，拉条布置影响其幅值；檩条的约束扭矩呈反对称分布，无拉条檩条整体平均值较小但局部峰值较大，拉条的布置较大程度减小了局部分布，但在布置拉条的区域出现较大的约束扭矩峰值。

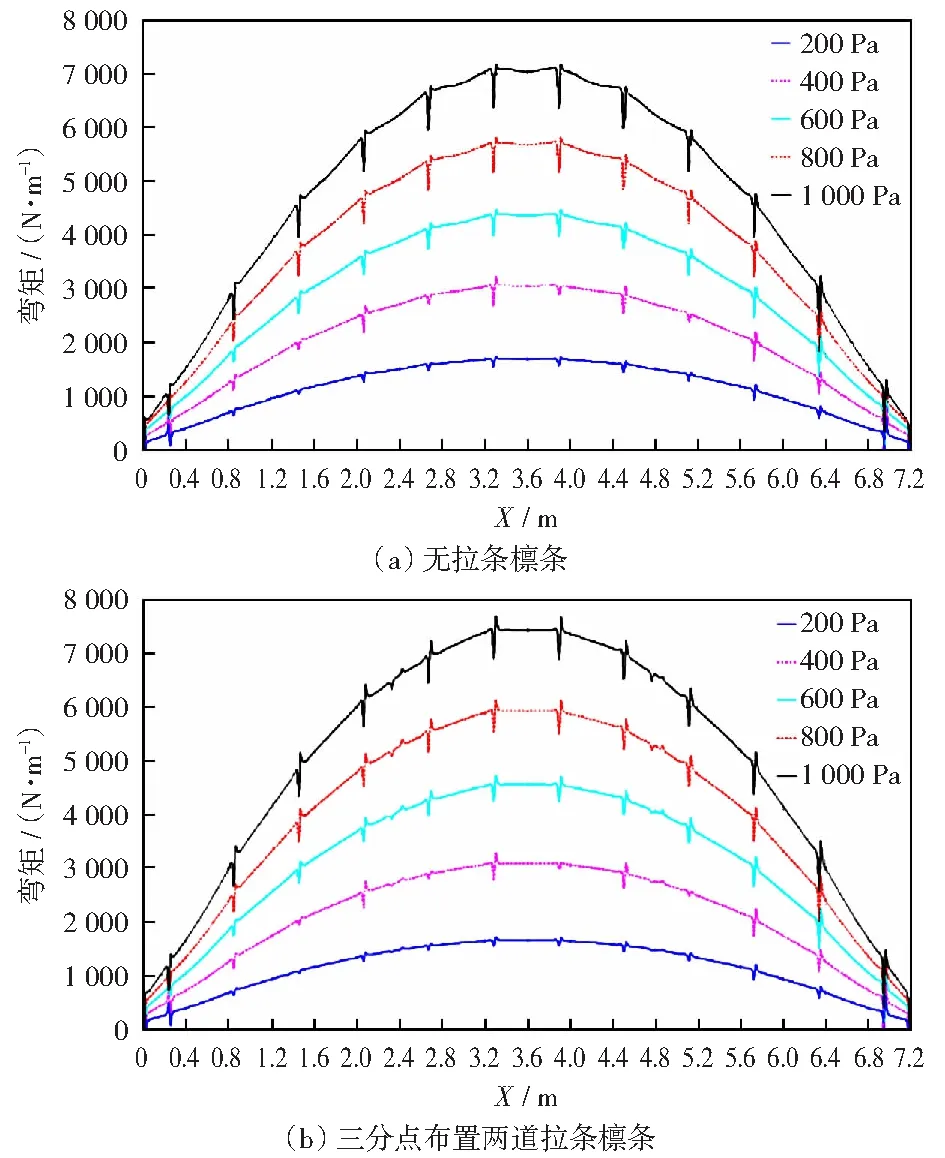
图20 平面内弯矩MxFig.20 In-plane moment Mx

图21 平面外弯矩MyFig.21 Out-plane moment My

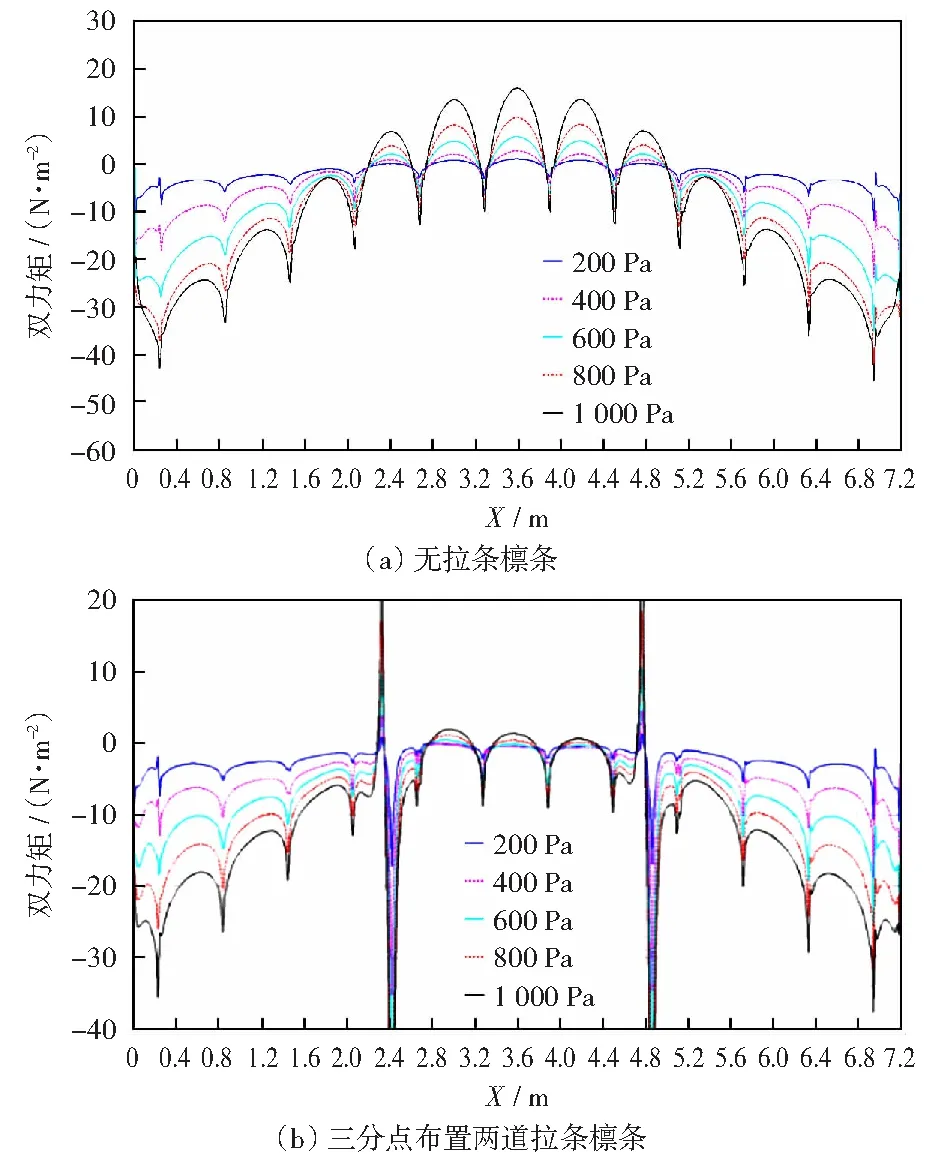
图22 双力矩BFig.22 Bimoment B

图23 约束扭矩MωFig.23 Restraint torque Mω

对屋面系统精细有限元模型，分别改变檩条跨度、拉条布置方式、屋面系统形式、支座形式得到檩条内力，分析各因素对檩条平面内弯矩、平面外弯矩、双力矩以及约束扭矩的影响。结果表明各参数对檩条内力产生了不同程度的影响，但总体趋势相似。檩条跨度影响内力整体分布但不影响局部分布；拉条布置方式对檩条内力分布的影响不大，但与未设置拉条存在区别；屋面板形式对檩条内力的分布和幅值几乎没有影响；半刚性连接和刚性连接下檩条内力比较接近，应当充分考虑半刚性连接平面内和平面外约束作用。

3 轻钢屋面系统精细化设计方法

3.1 屋面支座连接件设计

支座连接件是直立锁缝屋面系统中重要的传力构件，其受到的风力可以表示为

Fu=PwAe.

(5)

式中：Pw为风压标准值，按《门规》[19]取值，该处考虑上海地区取0.55 kN/m2，Ae为有效受风承载面积，同传统风荷载从属面积Ac对应起来，引入一个调整系数η=Ae/Ac，即计算固定支座风荷载的放大系数。因此，对屋面支座连接件进行受力分析，可以看作是风荷载的放大系数的合理取值问题。

根据风洞试验中已有测点的风压时程，通过本征正交分解法获得有限元模型表面各节点的风压时程，输入到模型中，迭代之后得到收敛解，计算系数η.结果表明，角部和边区随着迭代次数的增加，得到的系数η的值增大，这是因为该区域脉动风压较大且风涡明显，迭代过程中实际的风压取代了本征正交分解得到的风压时程；中间区迭代过程中η值逐渐减小，因为该处脉动风压和平均风压都较小，一些较小的数据被本征正交分解得到的值取代。

表5 各工况放大系数η最大值Table 5 Maximum value of η in different cases

表5给出了在三个工况(长宽比分别为1∶1，2∶1，3∶1)下各区域选取的典型支座中η的最大值，黑体为各区域最大值。可以看出，支座的有效受风承载面积Ae比从属面积Ac大，长宽比对角部和边区的取值影响较小；但对于中间区域，当长宽比达到3∶1时，风压分布更为均匀，放大系数η取值较小。

为保证实际工程中的安全性，三个分区的放大系数η取分析结果的最大值。研究表明[22]斜风向下，背风屋面和墙面的负压随着长跨比的增大而显著增大，迎风墙面的平均风压受几何尺寸的影响较小，因此当长宽比大于3时，取等于3的情形。基于理论分析和动力时程分析，得到支座有效受风承载面积同从属面积比值η=Ae/Ac，即放大系数，取值如下：角部η=1.7，边区η=1.4，中间区η=2.0，分区方式采用《门规》[19]关于固定支座风荷载体型系数分区的规定。

3.2 檩条的精细化设计

前述分析表明檩条的承载性能与屋面系统约束情况、檩条跨度、拉条布置方式等因素有关，截面类型和钢材屈服强度也是檩条的设计中需要考虑的问题。现对檩条承载性能开展进一步的参数分析，将各部分影响量化，参照我国规范[17]中檩条稳定承载力的计算公式，提出考虑屋面系统实际约束作用的檩条承载力简化计算公式：

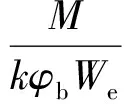
(6)

式中：M为檩条腹板平面内的弯矩；φb为稳定系数，按GB 50018[17]计算；We为关于垂直腹板轴的有效截面模量；k为考虑屋面系统约束作用的稳定系数修正系数，按下式计算：

(7)

式中：L为檩条跨度，m；h为檩条截面高度，mm；t为檩条厚度，mm；a，b，c为系数，取值由参数分析结果归纳得到，如表6和7，括号内的取值为仅考虑屋

表6 Z形檩条稳定系数修正系数k计算参数取值Table 6 Calculation parameters for k of Z purlins

面系统扭转约束作用而不考虑侧向约束作用的保守取值。kφb即为相对于有效截面屈服弯矩Mye=We·fy的折减系数Rf，将计算出的结果与根据有限元模型计算得到的结果RA进行对比，二者平均误差小于5%，结果较准确。考虑到基本试验法的使用条件，该建议公式仅适用于檩条与本文研究的两类直立锁缝屋面系统连接的情况，且屋面板和支架滑动片厚度不应小于开展足尺试验中的厚度，若不满足厚度要求可忽略屋面系统的侧移约束作用，仅考虑扭转约束作用，其刚度采用公式(3)计算。

表7 C形檩条稳定系数修正系数k计算参数取值Table 7 TCalculation parameters for k of C purlins

与我国现行规范公式计算结果相比，对于不设拉条的檩条，由于规范公式未考虑屋面系统的约束作用，计算结果过于保守；对于设有1道拉条的檩条，建议公式计算结果普遍略高于规范公式计算结果，但二者差别不大；对于设有2道拉条的檩条，C形檩条的计算结果非常接近，Z形檩条采用建议公式与规范公式计算结果的平均比值为0.9左右，规范公式计算结果偏不安全。

4 结语

本文结合试验研究、理论分析、数值分析等方法，对轻钢屋面系统的风荷载进行了深入研究，提出直立锁缝屋面系统固定支座和主体结构有效静力风荷载的估计方法，并对直立锁缝屋面系统中轻钢檩条的承载性能进行了全面系统的研究，分析屋面系统对檩条的约束机理并提出风吸力作用下檩条承载力实用简化计算公式，得出以下主要结论：

1) 对双坡屋面刚性模型进行风洞试验研究，两次试验研究表明，风洞试验结果是合理的，可以为后续的理论分析和动力时程分析提供数据。

2) 基于理论分析和动力时程分析，通过相对传统风荷载从属面积的放大系数η将有效受风承载面积的概念引入到固定支座的有效静力风荷载的估计中。

3) 风吸力下直立锁缝屋面系统中檩条的破坏模式主要与拉条设置状况有关。檩条跨度、屋面系统和支座形式也在一定程度上对檩条的内力有影响。

4) 两类典型直立锁缝屋面系统的扭转约束刚度主要与支架滑动片厚度和屋面板厚度有关，基于参数分析结果提出的实用简化计算公式适用于分析屋面板厚度和支架滑动片厚度在常用范围内时两类屋面系统的扭转约束刚度。给定扭转约束作用下檩条的承载力随侧移约束刚度增加而增大，直至侧移约束刚度达到某一门槛值时承载力不再继续增大。

5) 对其他直立锁缝屋面系统对檩条的约束刚度进行研究，提出了更为普遍的分析方法，并与给出的扭转刚度计算公式进行对比验证其合理性。

6) 针对风吸力作用下直立锁缝屋面系统中轻钢檩条的承载性能，提出了考虑屋面系统约束作用的檩条承载力简化计算公式，式中屋面系统为檩条提供的约束作用通过对受弯构件整体稳定系数φb乘以修正系数k体现。