冷弯型钢檩条屋面增设光伏板的下撑式檩条结构加固受力性能分析及改造方案

佘远善,陈颢元,郭耀杰

(武汉大学土木建筑工程学院,武汉 430072)

当前能源紧缺和环境污染是人类广泛关注的两大世界性问题,为了缓和与解决这两大问题,必须加以开发和利用新型清洁能源。而太阳能就是一种最普遍的可再生清洁能源,为有效利用太阳能资源,政府对屋顶分布式光伏板发电项目进行了大力推广[1]。

轻钢厂房屋面面积大,阳光辐射量充足,极适合铺设光伏板进行发电。然而铺设光伏板势必引起屋面恒载增大,导致原屋面檩条常出现承载能力不足问题[2]。此时必须对屋面檩条进行改造加固,加固后方可在厂房屋面上铺设分布式光伏板发电系统。为减少拆除屋面板等施工程序,避免材料浪费和减小工程量,文献[3]提出为檩条设置缀板的加固方法。该方法能够使檩条的破坏形式由弯扭屈曲破坏改变为弯曲破坏,从而提高构件的承载力。但对于弯曲破坏控制的檩条,增设缀板所引起的截面变化对抗弯刚度影响并不大。文献[4]指出,通过薄壁钢板将简支檩条连接加固为连续檩条,能使檩条极限承载力有一定程度提高。文献[5]指出,下撑式檩条在相同条件下用钢量相比一般钢结构可节省1/3～1/2。

目前,针对下撑式檩条结构的受力性能研究鲜见报道。现提出一种下撑式檩条结构对原屋面檩条进行改造加固,对加固后影响下撑式檩条受力性能的主要因素进行分析,并总结出其变化规律。以期提出更为经济的改造方案,以便于实际工程应用。

1 下撑式檩条

轻钢厂房屋面檩条常采用冷弯薄壁C型钢,当屋面板刚度较大且与檩条连接牢固时,不必计算其整体稳定[6]。实际工程中屋面板常选用压型钢板,钢板与檩条之间利用自攻螺钉连接,可不计算檩条的整体稳定性,此时可认为檩条的破坏形式为弯曲破坏。

针对檩条的弯曲破坏,提出一种下撑式檩条结构加固方法,即为檩条设置两根撑杆,撑杆下端由拉条支撑,拉条固结于檩条两端或端部钢梁,如图1所示,正视图为结构的左半部分,整体图形可通过对称得到。撑杆与檩条采用焊接连接,撑杆下端钻孔使拉条穿过,拉条两端采用焊接方式固结。

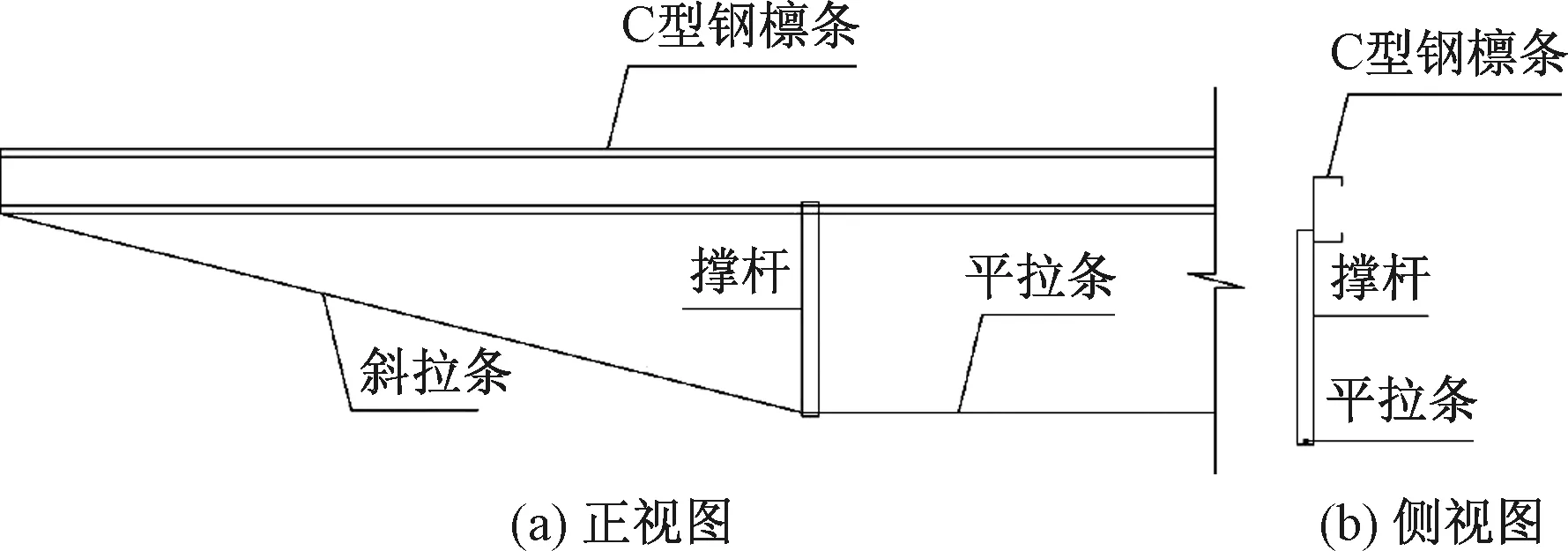
图1 下撑式檩条加固方法示意Fig.1 Outline of reinforcement method of down-stayed purlin

2 下撑式檩条有限元模型的建立与调试

2.1 檩条相关参数及设计荷载

根据某轻钢工业厂房实例,屋面冷弯型钢檩条相关参数如表1所示。铺设光伏板后,檩条恒荷载增加,由原来的0.5 kN/m2增大到1 kN/m2[7],檩条活荷载仍为0.5 kN/m2,不考虑风荷载作用。除考虑重力荷载作用外,施加在檩条上的荷载设计值为2.85 kN/m。

表1 檩条相关参数Table 1 Purlin related parameters

2.2 有限元模型

对于下撑式檩条结构,当撑杆间距变化时,撑杆始终关于檩条跨中截面对称布置,而撑杆均采用方钢管,仅截面尺寸发生变化。拉条均采用热轧带肋钢筋,仅截面直径发生变化。撑杆与拉条的弹性模量和密度均与檩条相同。考虑到工程实际,初步选定撑杆长度为500 mm,撑杆间距选取为檩条跨度的1/3,即2 000 mm,其他相关参数如表2所示。利用ANSYS软件建立下撑式檩条有限元模型时,根据各构件参数建立几何模型,檩条和撑杆构件采用beam189单元,拉条构件采用link180单元。对于边界条件的设置,考虑屋面能阻止檩条侧向位移和扭转[8]的情况,建模时约束了檩条所有节点的横向位移和绕纵轴的转动,其他约束条件与一般简支梁结构类似。建立的下撑式檩条结构有限元模型如图2所示。

表2 撑杆及拉条参数Table 2 Parameters of strut and brace

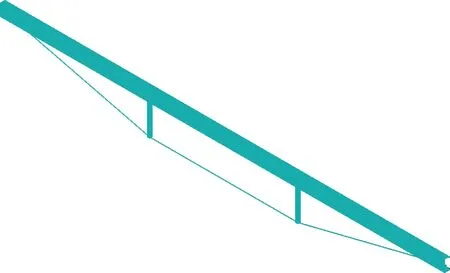
图2 有限元模型Fig.2 Finite element model

2.3 有限元模型的调试

为验证下撑式檩条结构能有效降低原简支檩条的应力水平,对本例中简支檩条在恒荷载增大前后及下撑式檩条在恒荷载增大后3种情况分别建立有限元模型并进行求解,得到的应力云图如图3、图4所示。

从图3可以看出,在恒荷载增大前后,原简支檩条最大应力由184.87 MPa增加到266.39 MPa,而檩条应力限值[9]为215 MPa,显然在恒荷载增加后,原有檩条确实出现了承载能力不足的问题。在铺设光伏板之前,必须采取措施对原有檩条进行改造加固。

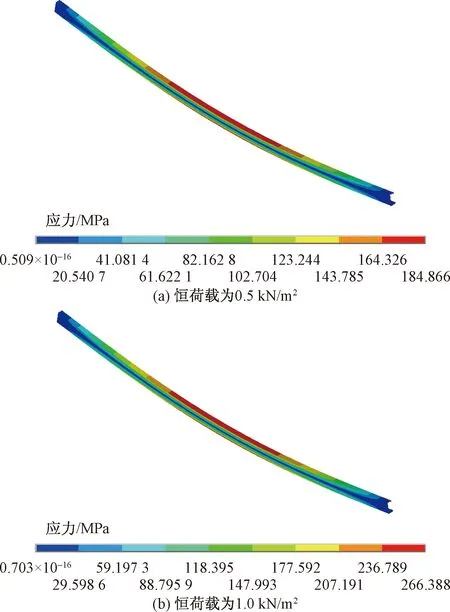
图3 恒荷载增大前后简支檩条的应力分布Fig.3 Stress distribution of simply supported purlins before and after constant load increases

从图4可以看出,采用下撑式檩条结构后,檩条构件最大应力仅为121.32 MPa,而相同荷载作用下的简支檩条最大应力为266.39 MPa,应力水平得到大幅降低,小于檩条应力限值。撑杆及拉条应力限值[9]分别为215、360 MPa,而应力云图中撑杆最大应力仅为73.13 MPa,拉条最大应力为320.80 MPa,均处于安全范围内。这表明下撑式檩条提高了原有檩条的承载能力,在加铺光伏板后,整体结构能够保证安全性,并且檩条构件应力得到了大幅降低,说明下撑式檩条改善原有檩条承载性能的效率是比较高的。

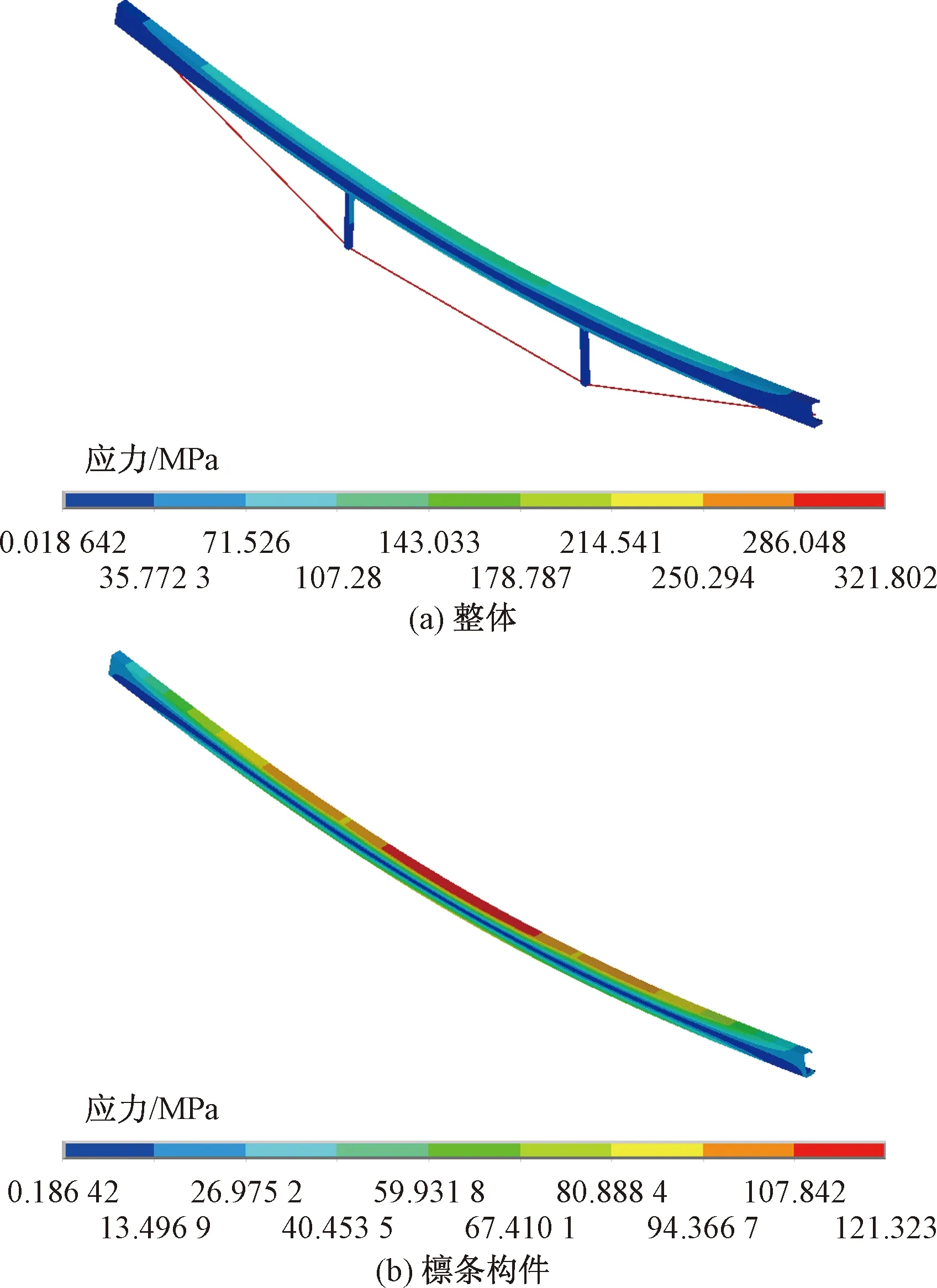
图4 恒荷载为1 kN/m2的下撑式檩条应力分布Fig.4 Stress distribution of down-stayed purlin with constant load of 1 kN/m2

3 下撑式檩条受力性能

下撑式檩条由檩条、撑杆和拉条组成,针对影响结构受力的主要因素,即撑杆长度、撑杆截面、拉条截面和撑杆间距,采用控制变量法来研究这4个因素对整体结构受力性能的影响。

3.1 撑杆长度的影响

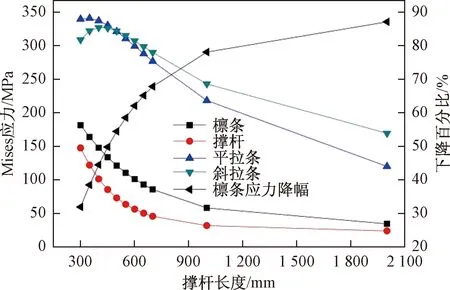
图5 撑杆长度与各构件最大应力的关系曲线Fig.5 The relation curve between the length of strut and the maximum stress of each member

从图5中关系曲线可以看到:随着撑杆长度的增大,檩条与撑杆构件的最大应力呈非线性减小,在撑杆长度小于1 000 mm前,曲线下降斜率较大,在撑杆长度大于1 000 mm后,曲线趋于平缓；而拉条最大应力随撑杆长度增大经历了一个上升段,之后同样逐渐减小,在撑杆长度较大时,相比于檩条及撑杆,其曲线下降斜率依然相当可观；下降百分比曲线变化趋势基本与檩条最大应力曲线相反,可以看到在撑杆长度大于500 mm时,檩条最大应力下降百分比均大于50%,应力水平改善效果明显。

下撑式檩条结构由于撑杆和拉条的存在,在檩条中会产生与外荷载作用引起的弯矩方向相反的弯矩,从而抵消了一部分外荷载弯矩,其原理类似于张弦梁结构,使得檩条应力相比于原简支檩条有所减小。而随着撑杆长度的增加,檩条及撑杆最大应力均呈减小趋势的原因在于:撑杆长度增加时撑杆中最大弯矩保持减小,而轴力持续增大,如图6所示。对于撑杆应力而言,弯矩的影响效应要比轴力更大,由于弯矩在减小,撑杆应力也就随之减小；对于檩条则是由于撑杆轴力增加引起了更大的反向弯矩,檩条应力减小幅度也就更大。拉条最大应力的变化情况要更复杂,因为斜拉条的轴力不仅受到撑杆轴力制约,同时也受到斜拉条与撑杆的夹角约束,撑杆轴力越大,斜拉条轴力越大,夹角越小,斜拉条轴力越小。撑杆长度增大时,撑杆轴力随之增加,而夹角随之减小。对于斜拉条轴力的变化趋势,在撑杆长度较小时,撑杆轴力是主要影响因素,于是斜拉条应力曲线在小撑杆长度区段存在一上升段,在撑杆长度较大时,主要影响因素变化为夹角,于是斜拉条应力曲线开始持续下降。平拉条应力曲线变化趋势与斜拉条是一致的。

图6 撑杆长度与撑杆弯矩及轴力的关系曲线Fig.6 The relation curve of strut length with strut bending moment and axial force

总而言之,撑杆长度增加时,各构件最大应力总体保持减小趋势,檩条最大应力下降比例则不断增大,下撑式檩条的结构优势也就越明显。然而,撑杆长度也不宜过大,否则会影响厂房室内净空以及产生撑杆稳定性问题,同时也不宜过小以免导致安装困难。撑杆长度建议设置在700 mm以下60 mm以上,具体关于最经济撑杆长度将在第4章中展开讨论。

3.2 撑杆截面的影响

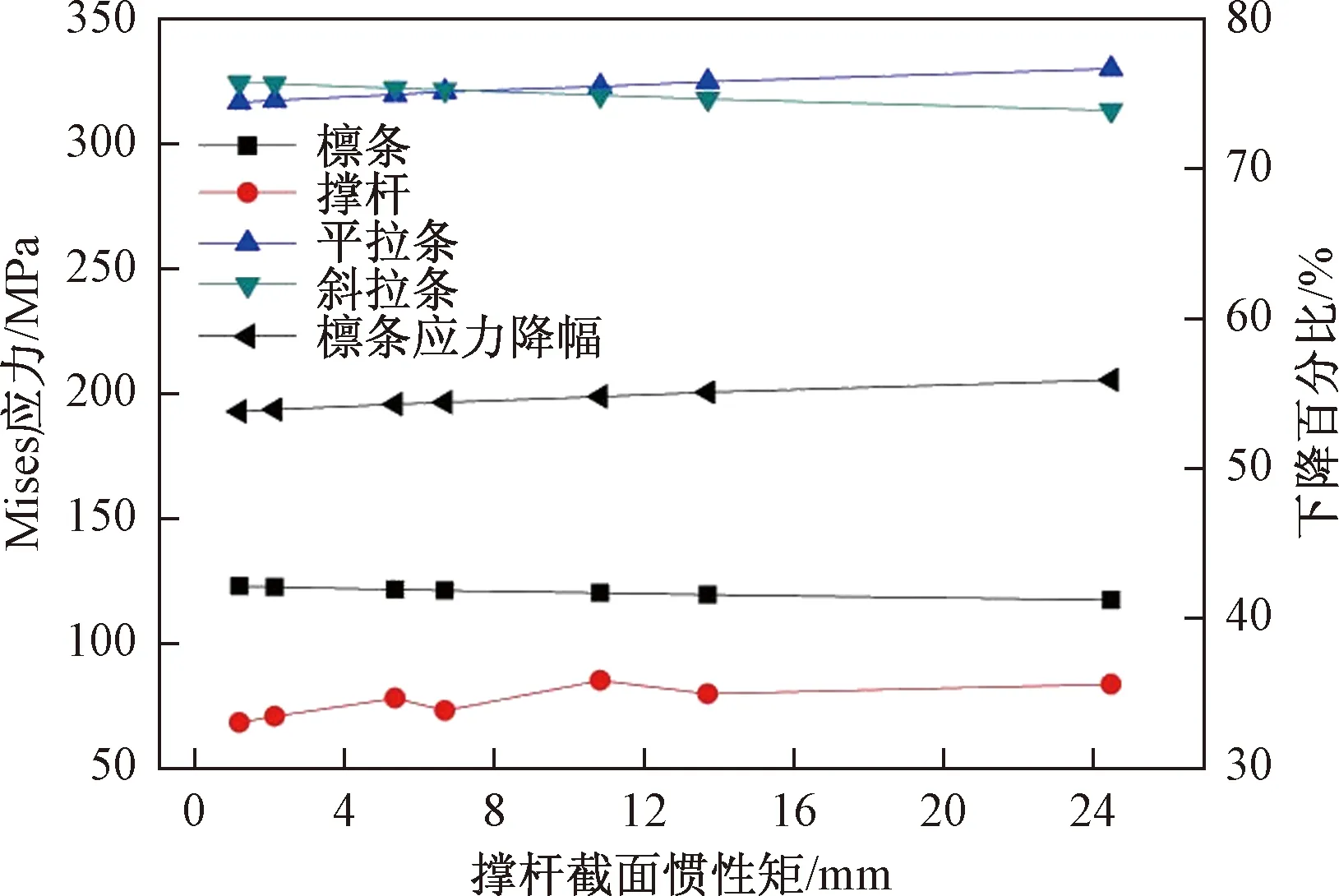
图7 撑杆截面惯性矩与各构件最大应力的关系曲线Fig.7 The relation curve between the moment of inertia of the strut section and the maximum stress of each member

从图7的关系曲线可以看出:在撑杆截面改变时,下撑式檩条各个构件的最大应力变化很小,关系曲线基本保持平缓。原因在于,随着撑杆截面变化使得截面惯性矩增加时,撑杆中最大弯矩也保持增大,撑杆中轴力则缓慢减小。由于撑杆轴力变化较小,檩条和拉条最大应力基本保持稳定；对于撑杆应力,尽管截面惯性矩在增大,但同时撑杆弯矩也在增大,最终导致撑杆应力变化也较小。总而言之,撑杆截面对于下撑式檩条整体结构受力影响程度很低,为减少结构自重,采用下撑式檩条结构进行加固时,撑杆截面可直接选用常见最小截面。

3.3 拉条截面的影响

为得到拉条截面对整体结构受力性能的影响规律,撑杆长度选取为500 mm,撑杆截面选取为40 mm×2.0 mm,撑杆间距选取为2 000 mm,通过不断改变拉条截面,得到不同拉条截面下各构件的最大应力,其关系曲线如图8所示。

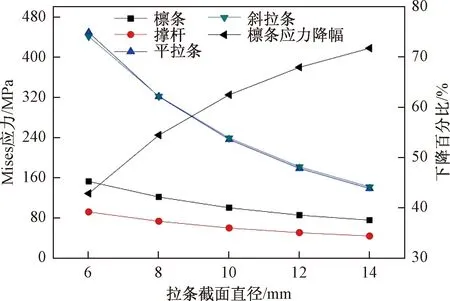
图8 拉条截面与各构件最大应力的关系曲线Fig.8 The relation curve between the brace cross section and the maximum stress of each member

从图8可以看到,随着拉条截面直径的增大,各构件的最大应力都呈非线性减小,其中斜、平拉条应力的曲线下降斜率较大,相比而言檩条及撑杆应力曲线变化趋势则更加平缓。尽管如此,檩条最大应力下降比例仍相当可观,拉条截面直径取为14 mm时,应力下降比例可达到70%。图8说明了拉条截面的变化对整体结构受力的影响一般,但对拉条构件本身的应力水平影响较大。拉条截面增大会导致结构自重及结构用钢量变大,在满足结构安全性的前提下,拉条应尽量采用较小截面。

3.4 撑杆间距的影响

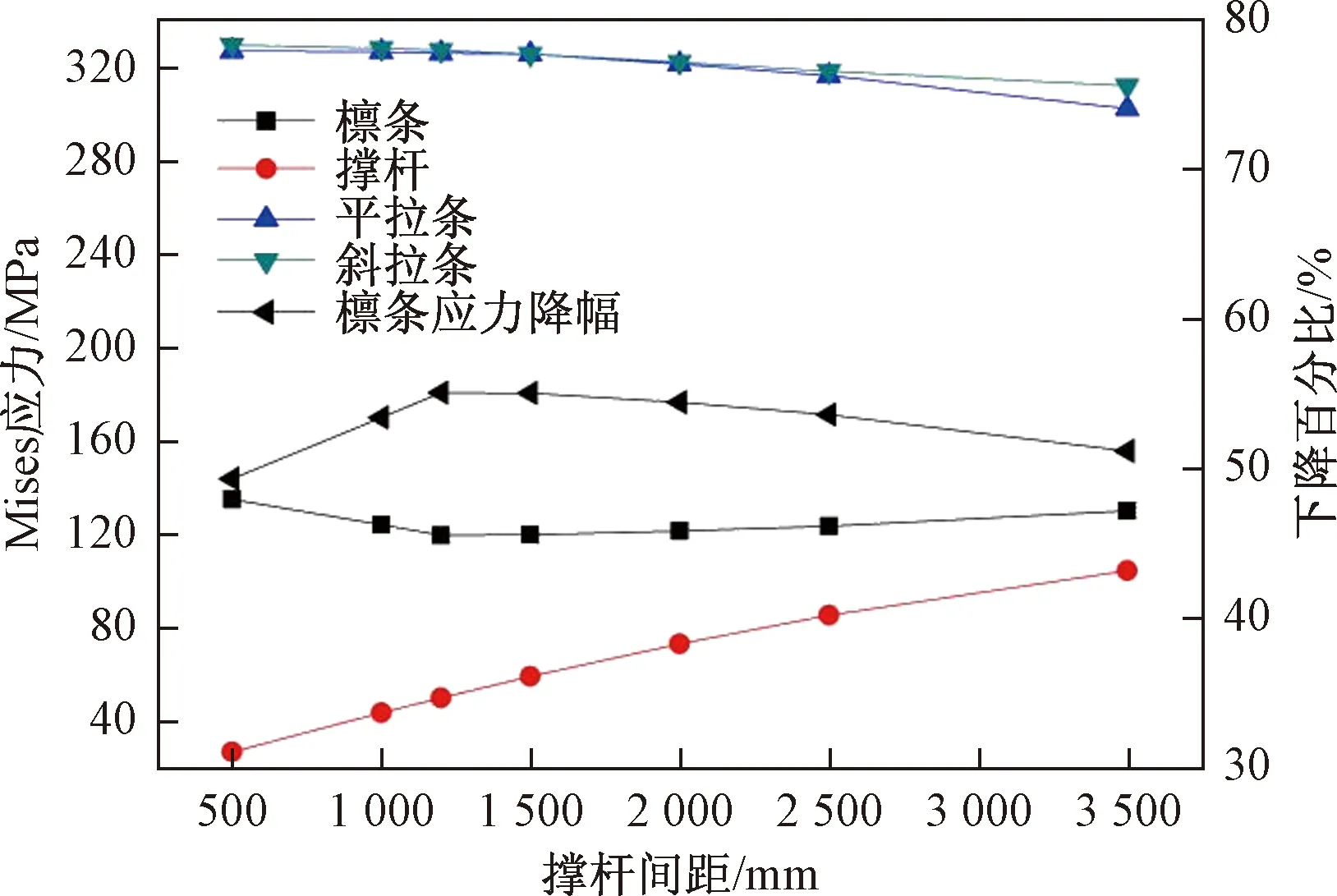
图9 撑杆间距与各构件最大应力的关系曲线Fig.9 The relation curve of the distance between struts with the maximum stress of each member

由图9可以看出:撑杆间距增大时,斜、平拉条最大应力呈非线性减小,但减小幅度不大；撑杆应力则随撑杆间距增大几乎呈线性增长；檩条应力随撑杆间距增加呈先减小再增大的变化趋势。采用下撑式檩条结构加固原简支檩条主要是为充分降低檩条应力水平,从这个目标出发,也考虑到其他构件应力水平宜较低,该算例檩条的最佳撑杆间距应选取为1 200 mm,若采用比例形式表达,檩条被撑杆划分出的三段长度比例为2∶1∶2,即最佳撑杆间距应取为檩条跨度的1/5。针对檩条跨度不同的情况,最佳撑杆间距采用比例形式表达更便于推广。

4 下撑式檩条改造方案

采用下撑式檩条结构加固原简支檩条,需要制定具体的改造加固方案,具体而言,就是确定出合适的撑杆长度、撑杆截面、拉条截面和撑杆间距。研究遵循经济性原则,即寻求使得改造用钢量达到最小的改造方案。根据各因素对整体结构受力的影响规律,结合某轻钢工业厂房实例,首先可确定出撑杆间距为1 200 mm。对于撑杆截面,由于其变化对各构件的最大应力影响很小,故可直接选用常见的方钢管最小截面,截面尺寸即为25 mm×1.5 mm。由于撑杆长度对整体结构受力影响程度较大,同时拉条截面对拉条应力影响大,对其他构件应力也有一定影响,在保证下撑式檩条结构安全性的前提下,这两个因素成为约束改造用钢量的主要变量。此时存在两种方案,一种是以撑杆长度最小为目标,不改变默认的拉条截面,通过不断减小撑杆长度,最终找到使得各构件最大应力均小于限值的最小撑杆长度,另一种则以寻求最小的拉条截面为目标,先将拉条截面替换为最小直径,然后通过不断调整撑杆长度使得各构件最大应力均能恰好小于限值。4个因素对整体结构受力性能的影响程度及各因素确定原则如表3所示。

表3 改造方案4个因素的影响程度及原则Table 3 The influence degree and principle of the four factors in the reconstruction scheme

4.1 撑杆长度最小方案

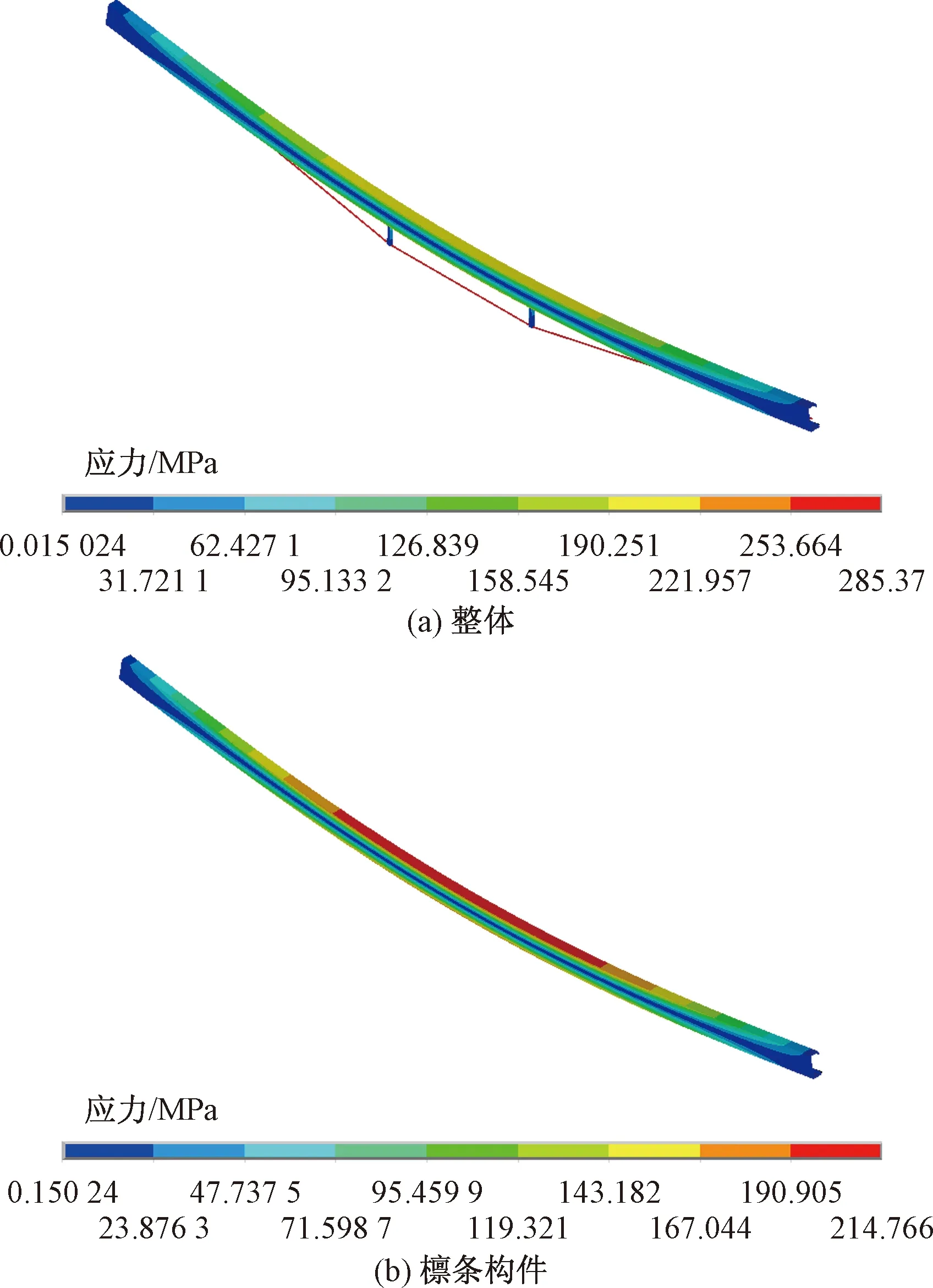
图10 撑杆长度为230 mm的下撑式檩条应力分布Fig.10 The stress distribution of the down-stayed purlin with the strut length of 230 mm

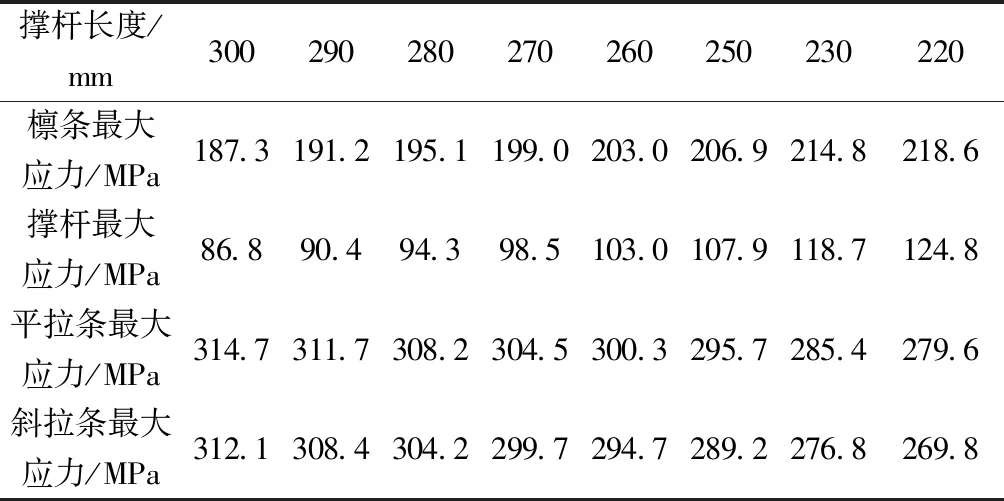
表4 撑杆长度最小方案的应力结果Table 4 The stress result of minimum strut length scheme

根据各构件材料标号,通过查阅钢结构设计标准[9]可知檩条及撑杆应力限值为215 MPa,拉条应力限值为360 MPa。根据表4的应力结果及各构件应力限值,易知撑杆长度最小可取得230 mm。

4.2 拉条截面最小方案

图11 拉条截面为6撑杆长度为1 220 mm的下撑式檩条应力分布Fig.11 The stress distribution of the down-stayed purlin with the strut length of 1 220 mm and the brace section of 6

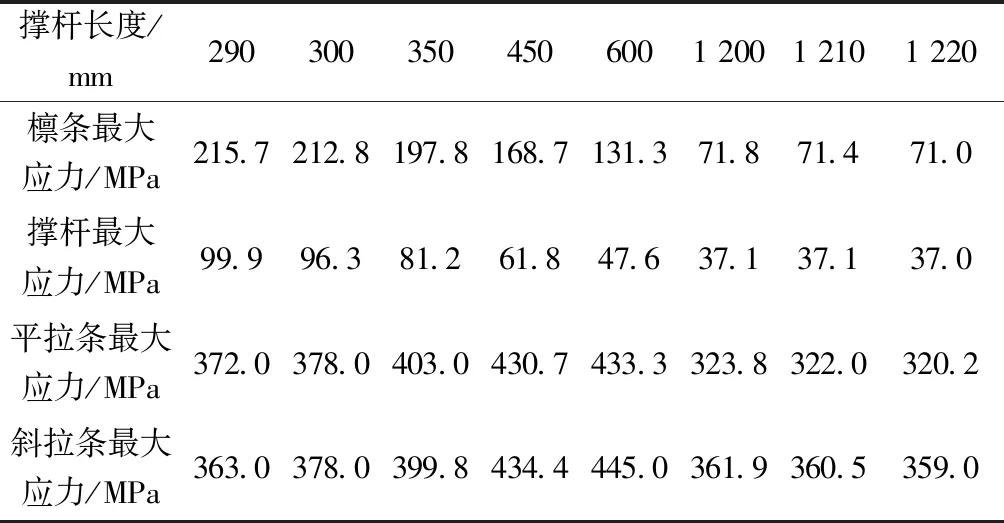
表5 拉条截面最小方案的应力结果Table 5 The stress result of minimum brace section scheme

4.3 两种方案对比及最终改造加固方案确定

为了得到最小改造用钢量加固方案,分别通过最小撑杆长度和最小拉条截面方案寻求到了4个因素的取值。两种方案的改造用钢量如表6所示。

由表6可以看出,相比于保证撑杆长度最小,替换更小拉条截面确实会使得拉条用量得到大幅度降低,然而由此也造成撑杆长度增加,最终导致整体改造用钢量变大,并且撑杆长度过大,会影响厂房室内净空及产生稳定性问题。显然在本例中,采取撑杆长度最小方案才能使改造用钢量取得最小值。

表6 改造用钢量计算表Table 6 Steel quantity calculation table for transformation

结合上述两种方案,最终改造加固方案可按照这样的方式确定:首先以撑杆长度最小为导向,对于某一初选撑杆长度,通过不断调整该长度,最终得到使下撑式檩条各构件应力恰好均小于限值的目标撑杆长度。若此时拉条应力水平相比于强度设计值具有相当的富足空间,例如拉条最大应力仅为300 MPa左右,可尝试替换更小拉条截面并对结构模型进行求解验证,经过微调撑杆长度后结构能够满足应力限值条件则说明缩小拉条截面是可行的。

5 下撑式檩条改造方案

针对不同檩条截面,不同檩条跨度及不同设计荷载的轻钢厂房屋面檩条的具体改造方案,可利用ANSYS进行扩展计算,通过应用最终改造加固方案而得到解决。由于撑杆间距和撑杆截面是相对确定的,其中撑杆间距始终选取为檩条跨度的1/5。而撑杆长度则根据跨度不同,结合前例按比例进行长度初选,拉条截面可先按默认设置不做调整,然后对初选模型进行求解,视拉条及檩条应力水平再调整模型参数直至其应力水平下降至限值以内,之后按照最终改造加固方案寻求最经济解即可。为方便设计人员快速选用及造价人员的初步估价,根据有限元仿真分析结果,针对部分典型檩条截面、檩条跨度和设计荷载,提出了可供快速选用的下撑式檩条改造方案推荐表供工程应用参考。改造方案推荐表如表7所示。

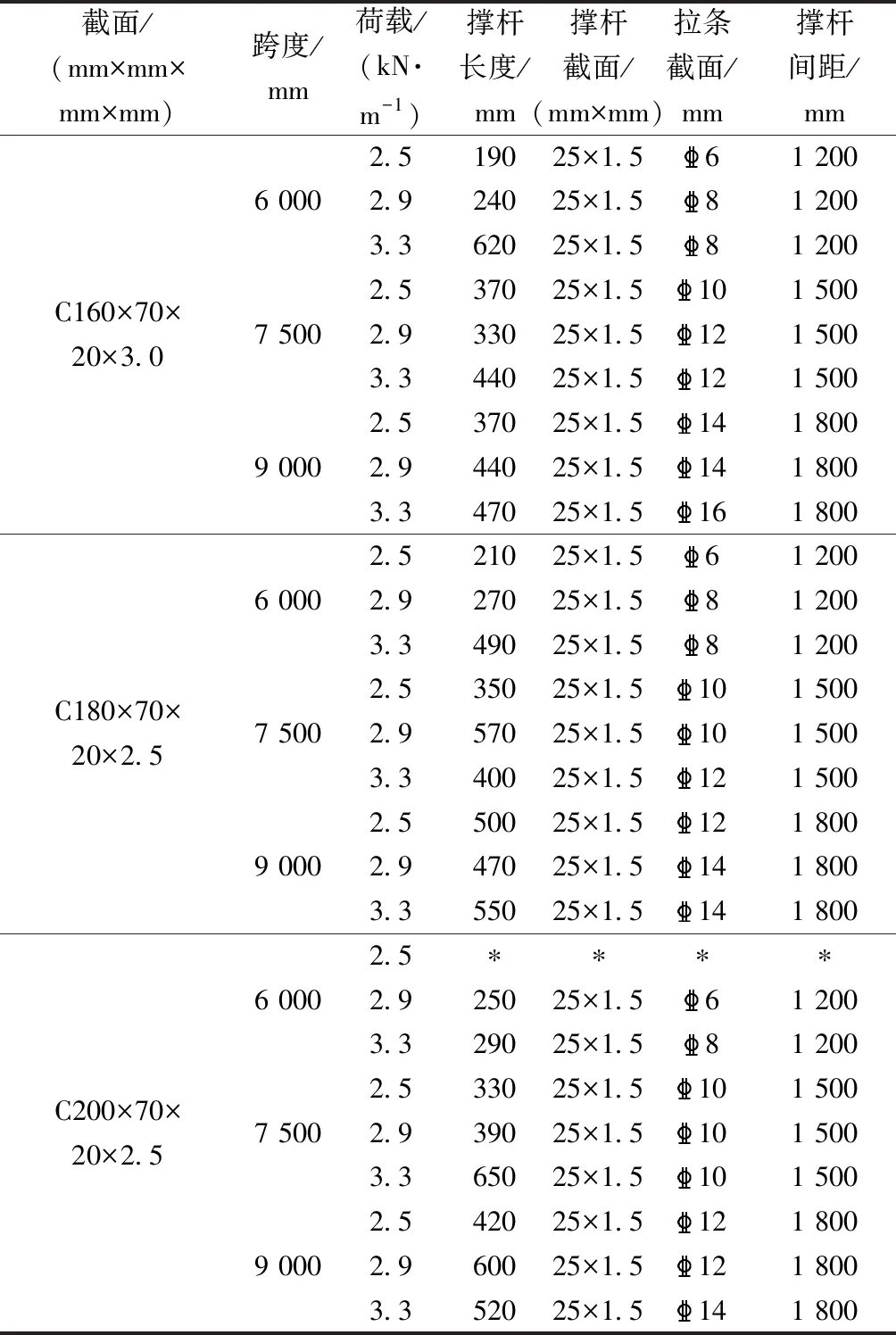
表7 下撑式檩条改造方案推荐表Table 7 Recommendation table of down-stayed purlin reconstruction scheme

需要指出的是,考虑到室内净空及撑杆稳定性等因素的影响,撑杆长度必须始终保持在700 mm以下。

对檩条设置拉条对于其侧向稳定具有重要作用[10-12],为保证改造后下撑式檩条结构的侧向稳定性,也可尝试在撑杆底端处设置拉条。

6 结论

针对轻钢厂房屋面檩条在加铺光伏板后将产生的承载能力不足问题,建议采用下撑式檩条结构对原檩条进行改造加固,利用ANSYS建立下撑式檩条结构的有限元模型,根据有限元计算结果,利用控制变量法,分析及总结了撑杆长度、撑杆截面、拉条截面和撑杆间距对整体结构受力性能的影响规律,并在此基础上进一步研究及提出了最终改造加固方案。得出以下结论。

(1)撑杆长度是下撑式檩条整体结构受力性能的主要影响因素,随着撑杆长度增加,檩条及撑杆应力均会大幅减小,拉条应力则呈现先增大再减小的趋势；拉条截面是下撑式檩条整体结构受力性能的次要影响因素,拉条截面直径越大,拉条应力越小,其他构件应力也减小,但应力曲线下降斜率较小；撑杆间距对各构件应力影响均较小,撑杆应力随撑杆间距增加几乎呈线性平缓增大,最佳撑杆间距为檩条跨度的1/5；撑杆截面对各构件应力水平影响均很小,为减少结构自重和改造用钢量,改造方案中撑杆截面应直接选取为常见最小截面。

(2)最终改造加固方案是按比例确定撑杆间距和按最小截面确定撑杆截面后,以撑杆长度最小为导向,对于某一初选撑杆长度,通过不断调整该长度,最终得到使下撑式檩条各构件应力恰好均小于限值的目标撑杆长度。若此时拉条应力水平相比于强度设计值具有相当的富足空间,例如拉条最大应力仅为300 MPa左右,可尝试替换更小拉条截面并对结构模型进行求解验证,经过调整撑杆长度(但始终应小于限值700 mm)后满足应力限值条件则说明缩小拉条截面是可行的。采用最终改造加固方案可使改造用钢量取得最小值。

(3)针对部分常见截面、跨度及设计荷载的轻钢厂房屋面檩条改造,利用ANSYS进行扩展计算,应用最终改造加固方案,根据有限元仿真分析结果提出了可供快速选用的下撑式檩条改造方案推荐表供工程应用参考。