LBSN中基于社区联合聚类的协同推荐方法

龚卫华 金 蓉 裴小兵 梅建萍

1(浙江工业大学计算机科学与技术学院 杭州 310023) 2(浙江理工大学信息学院 杭州 310018) 3(华中科技大学软件学院 武汉 430074)

近年来，随着各种移动社交应用与位置服务的紧密融合，催生了一种新的异质信息网络——基于位置的社交网络(location based social network, LBSN).LBSN通过用户在位置上的签到功能把线上虚拟社会与线下物理世界关联在一起.举例说明，FourSquare，FacebookPlaces，Yelp等不仅具备传统社交网络的社交功能，还能衍生多种与位置相关的服务，比如位置共享、兴趣点(point of interests，POIs)推荐、朋友或近邻推荐等，从目前趋势来看，面向LBSN的推荐技术已成为推荐系统领域最活跃的研究分支之一.

众所周知，数据稀疏性一直是影响传统推荐质量的关键难题之一，LBSN中的兴趣点推荐和朋友推荐在此面临着更大的挑战.一方面是由于LBSN中的用户-位置签到矩阵是极端稀疏的，在LBSN中通常包含有数百万的兴趣点，用户日常活动具有空间局部性，一些热点位置如景点、餐馆等地方容易受到大量用户的关注，而对于每个用户所能访问的兴趣点数量又十分有限.另一方面，LBSN中的用户社交关系也是高度稀疏的，由用户社交关系形成的社交网络一般都具有小世界现象和无标度特性，这些规律表明极少量的用户拥有较多的关系连接，而大量的用户仅具有少量的关系连接.大量研究发现,深入理解并掌握LBSN中的社区结构是有效缓解数据稀疏性的新途径，由于现实世界的许多网络都普遍存在着社区结构特征，该结构所潜在的信息传播能力、影响力等特性对于改善推荐性能具有重要意义，比如同一社区内有社交关联的用户往往会表现出相似的兴趣爱好和签到行为特征，又比如地理位置相近、关注兴趣点相同的用户比较容易聚集成社区群体，并且同一社区内的用户会对其他用户的选择产生一定的影响等.

目前，在传统社交网络领域虽然已有许多社区发现成果，但对其拓展的异质网络结构如LBSN中的复杂社区研究却非常匮乏.总的来说，现有研究大多将社交网络从图聚类或分割角度提出一些以节点为中心或边为中心的社区发现方法，由此得到的社区结构大致有2类：非重叠的社区与重叠的社区.非重叠的社区认为每个节点或用户只能属于一个社区，社区之间没有重叠.而在重叠社区中，用户可以隶属于多个社区，并且可以与多个社区内的用户关系都十分紧密.相比之下，重叠社区能够更真实地反映用户在现实网络中用户群体兴趣特征与行为规律，从而使得这种结构具有更广、更准确的推荐范围和能力.现阶段主流的重叠社区发现方法有基于团渗透的方法[1-2]、基于链接划分的方法[3-4]、基于标签传播的方法[5-7]、基于局部扩展与优化的算法[8-11]等.然而，这些研究都存在一些局限性：一是无法准确表达社区重叠部分的模糊性；二是这些方法都是针对同构的网络结构而言，而无法适用于LBSN这种包含多模实体及多维关系的异质网络.为此，本文的研究动机主要表现在：一方面是针对社区重叠边界的不确定性问题，我们采用基于非负矩阵分解的模糊聚类方法更加准确地刻画重叠社区结构特征；另一方面，由于LBSN比传统社交网络不仅仅是增加了位置维度，还包含了多种异质关系，因而亟待提出一种新的融合用户与位置实体及其多维关系的社区发现方法.

本文的主要贡献包括3点：

1) 提出了基于非负矩阵分解的联合聚类方法获得LBSN中紧密关联的用户模糊社区与兴趣点聚簇结构，有效缓解了朋友推荐和POI推荐中的数据稀疏问题.

2) 融合了LBSN中用户与位置这2类实体及其多维异质关系，主要包括用户间的社交关系、用户-位置签到关系、地理位置相似关系(即考虑了距离和标签因素的兴趣点特征).

3) 在Gowalla和Foursquare(NYC)数据集上的实验结果表明，本文提出的MRNMF(multi-relational nonnegative matrix factorization)方法同时在朋友与兴趣点这双重推荐上比其他传统方法具有更优越的推荐性能.

1 相关工作

重叠社区已被发现广泛存在于各种社交网络中，现有针对重叠社区结构的研究从采用的模型或方法上主要分为模糊的与非模糊的社区发现算法，其中非模糊的重叠社区发现研究一直是大多数国内外学者关注的热点方向.如引言中基于团渗透方法的主要思想是将社区视为由一些团(全连通子图)构成的集合，这些团之间通过共享节点而紧密连接，代表性算法如CPM[2].基于链接划分方法是将链接而不是节点作为考虑对象，通过设计适当的划分策略来获取链接社区结构，典型的算法有DBLC[3]和DBLINK[4].基于标签传播方法是一种半监督学习方法，主要是利用已标记节点的标签信息，通过已标记节点和未标记节点的相似度连边权重预测未被标记节点的标签信息，最常见的算法如LPA[5]，SPLA[6]，LPPB[7]等.基于局部扩展与优化的算法是利用网络的局部特性不断挖掘网络中的社区结构，例如LFM[10]，OSLOM[11]等都是该方法的典型代表.不难发现，这些方法的共同缺陷是无法恰当表达重叠节点在多个社区中的隶属强度，同时也没有考虑多维关系的融合而得到比较单一的社区结构.

另一种以模糊聚类理论为代表的重叠社区发现研究成果已表明，模糊重叠更符合真实社交网络的实际情况，该类方法的经典算法如FCM(fuzzy c-means)[12]最早应用于社交网络的模糊重叠划分，通过将重叠社区检测建模成目标函数的最小化问题：

(1)

(2)

易知，模糊划分的要点是允许节点以不同的隶属度值归属于多个社区，然而，由于FCM在聚类中仅考虑了节点距离特征因而丢失了网络图结构信息.此后，有一些文献[13-14]提出了一种结合模块度函数的FCM聚类方法发现网络中的重叠社区，但其缺点是社区结果依赖于随机游走值和模糊因子.

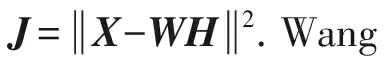
此外，NMF方法也特别适合发现重叠的社区结构，Zhang等人[22]提出基于对称矩阵分解的SBMF模型发现重叠社区结构，并通过划分密度方法自动确定合适的社区个数，该模型不仅能够明确划分网络的社区结构，还能提供节点与社区的隶属强度.文献[23-24]都提出了基于贝叶斯的NMF方法发现网络中的重叠社区，采用软划分方式有效刻画节点对多个社区的隶属程度.还有文献[25]提出了基于偏好的非负矩阵分解模型PNMF，在重叠社区发现中融入了链接偏好信息.

综上可知，现有大多数传统的NMF方法基本上都使得被分解的2个低维矩阵具有共同的维度空间，这种矩阵分解方式仅适于发现同构网络中的单一社区结构，也缺乏有效融合已知先验知识与多维关系或特征的方法.因此，另一些研究提出了改进的非负矩阵分解方法实现联合聚类，最早由Ding等人[26]提出了正交非负矩阵三分解的联合聚类方法，其表示形式如X≈FBZT，其中F表示行聚类的指示矩阵，而Z表示列聚类的指示矩阵.还有文献[27]也提出有限的非负矩阵三分解方法BNMTF发现重叠社区，其表示形式如X≈UBUT，其中U表示节点对社区的隶属度矩阵，而B表示社区间的交互矩阵.这些基于NMF的联合聚类方法虽具有比较理想的异质关系数据处理能力，但遗憾的是，迄今针对多模异质网络的社区发现研究仍十分缺乏，特别是对LBSN中的复杂社区结构没有深入的认识与理解.

受上述工作启发，本文将针对LBSN这种新型的异质网络提出一种基于NMF的融合多维异质关系的联合聚类模型，不仅能获得准确的用户模糊社区，同时还能得到关联的兴趣点聚簇，该紧密结构有助于提高朋友推荐与兴趣点推荐的质量.

2 LBSN的定义与模型表示

LBSN是一种由用户与地理位置这2种实体及其多维关系复合而成的异质网络，如图1所示.在图1中LBSN分别由用户层和地理位置层组成，上层为传统的用户社交关系网络，下层为地理位置标签网络，上下层之间通过用户-位置签到行为建立起异质实体间的联系.

Fig. 1 Structure of composite relational networks in LBSN图1 LBSN中的复合关系网络结构

为了描述LBSN的形式化模型，首先给出相关的定义：

定义1.用户社交关系网络.在同一用户层的用户间社交关系形成的网络可表示成一个无向图结构，记为S=(Y,E)，其中，Y表示用户集，E表示用户社交关系的边集，即E={(yi,yj)|yi,yj∈Y}.

定义2.用户-位置签到网络.用户在地理位置上的签到行为形成的关系网络可表示成二部图结构，记为P=(Y,D,T)，其中，Y表示用户集，D表示地理位置集，T表示用户与位置间的签到关系集，即T={(yi,dj)|yi∈Y,dj∈D,Y∩D=∅}.

定义3.地理位置标签网络.地理位置标签网络可抽象成一个无向图，记为G=(D,C)，其中，D为地理位置集合，C表示地理位置间的关系边集，即C={(di,dj)|di,dj∈D}.

在此基础上，本文进一步给出融合定义1～3的3种关系的异质复合网络模型即基于位置的社交网络的形式化定义.

定义4.基于位置的社交网络.是一种由用户与地理位置实体及其多维关系构成的异质网络图，记为WLBSN=S×P×G=(Y,E)×(Y,D,T)×(D,C)=(Y,D,E,T,C)，其中包含了2种实体：用户集Y与地理位置集D，与对应的3种维度关系：用户间的社交关系E、用户与位置的签到关系T、位置间的相似关系C.

在LBSN的用户层中，对于给定的用户集合Y={y1,y2,…,yn}，用户之间的相似性可通过检测社交关系网络S中是否具有共同朋友进行评估，于是我们采用Sorgenfrei系数来度量用户社交相似性：

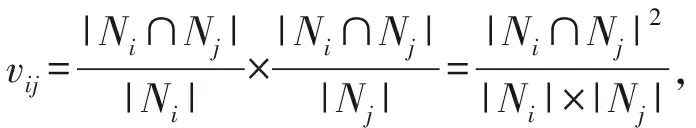
(3)

其中，Ni与Nj分别表示用户yi与用户yj的邻居集合.由此可见，用户社交关系形成的相似性矩阵可表示为V=(vij)n×n.

对于LBSN的地理位置层，地理空间上分布的位置集合有D={d1,d2,…,dm}，各位置间的相似性不仅直接与其空间距离特性相关，还与位置上的语义标签属性密切关联，我们综合考虑这2种因素给出地理位置相似性的定义：

(4)

其中，f(di,dj)表示位置di与dj间的欧氏距离，s(di,dj)∈[0,1]表示位置di与dj的标签相似性.因此，由地理位置相似关系构成的位置特征矩阵可记为O=(oij)m×m.

3 融合多维异质关系的联合聚类模型

在第2节所述的LBSN模型基础上，本文提出一种基于非负矩阵分解的用户模糊社区发现与兴趣点聚簇方法，采用三因子矩阵分解的表示形式如R≈UHL，将用户-位置关系矩阵R的行和列同时聚类分解为3个矩阵U，H，L.其中，U与L分别为用户端和位置端的聚类指示矩阵，H为关联矩阵.该方法的目标是在把原始矩阵映射到低维特征空间过程中既考虑了用户-位置签到关系，又融合了传统的用户社交关系与地理位置的兴趣点特征.

为了使矩阵分解的误差最小化，我们构造的目标函数为

(5)

在式(5)表示的非负矩阵分解模型中，用户对位置的兴趣偏好特征由用户-位置签到关系矩阵R表示，该矩阵从行聚类和列聚类角度被同时分解成关于用户端的隶属矩阵U与地理位置端的隶属矩阵L，从而以更直观的形式表明了用户兴趣模型不仅会受到用户重叠社区结构的影响，还与位置聚簇特征密切相关.本质上看，用户社区结构源于用户间内在的社交关系，而位置聚簇结构则依赖于兴趣点特征的相似性.

为了进一步考虑多维关系特征的影响，我们在式(5)的基础上提出一种新的融合社交关系与兴趣点特征的矩阵分解模型，整体目标函数为

(6)

为了求解目标函数的局部最优值，采用随机梯度下降法(SGD)分别对U，H，L求导可得：

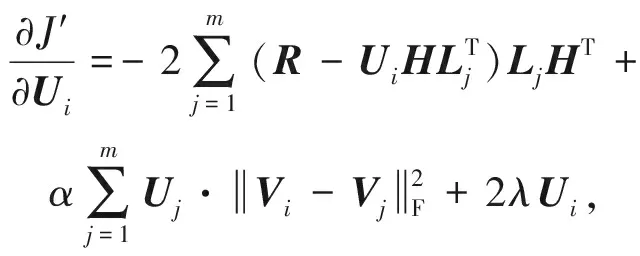
(7)

(8)

(9)

其中，式(7)与式(9)中的特征矩阵V与O分别由式(3)与式(4)计算而得，然后再根据式(10)～(12)迭代更新矩阵U，H，L的值，符号τ表示梯度下降迭代次数，μ>0表示学习速率.最终目标是使得所求矩阵U，H，L沿梯度下降方向不断迭代更新直至收敛或设定的阈值为止.

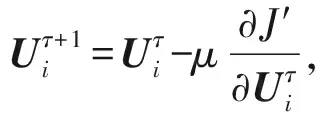
(10)

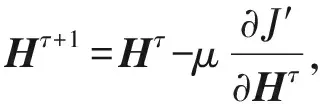
(11)

(12)

4 实验与结果分析

本实验的运行环境为Intel Core i7-4500U处理器、16 GB内存、Windows 7操作系统，算法采用Python2.7编程实现.下面分别给出了实验数据集描述、评价指标与实验结果分析.

4.1 实验数据集与对比方法

我们选取2种真实的数据集Foursquare (NYC)和Gowalla，验证本文所提方法的联合聚类效果与推荐性能.实验前先过滤数据集以移除一些异常数据，对于Foursquare(NYC)数据集，我们筛选出超过2人签到的地理位置，以及评论数多于5条的用户及其所拥有的社交关系.在Gowalla数据集中，我们筛选出签到数超过50的地理位置，以及社交关系超过50条且签到次数也超过50的用户.预处理完成后，各数据集中用户数、位置数以及社交关系和签到关系等基本信息如表1所示:

Table 1 Basic Information of Two LBSN Datasets表1 2种LBSN数据集的基本信息

从表1中可以看出，数据集Foursquare (NYC)与Gowalla上的用户签到密度都非常低，反映了LBSN中的兴趣点有较大的稀疏性，而在用户社交关系上，这2个数据集的社交用户平均度分别约为9.2和14.1，表明社交用户间的交互关系比较密切.

为了评价各方法在推荐性能上的差别，我们选取4种代表性的方法进行实验对比：

1) FCM方法.FCM是一种经典的基于模糊聚类的方法，文献[12]使用该方法发现复杂网络中重叠的社区结构.本实验中FCM方法仅从用户社交关系维度检测社交网络中的重叠社区结构，式(1)中的系数m=2.

2) NMF方法.NMF是由Lee等人[15]提出的一种非负矩阵分解方法，其形如X≈WH，该方法可用来发现社交网络中的重叠社区结构.本文将用户社交关系矩阵分解为2个对称的用户社区隶属矩阵，即为X≈HHT.

3) NMTF方法.Ding等人[26]提出了非负矩阵三因子分解的联合聚类方法NMTF，其表示形式如X≈FBZT，该方法在LBSN的用户重叠社区发现过程中仅考虑结合了用户社交关系与签到关系这2种信息.

4) MRNMF方法.MRNMF是本文提出的社区联合聚类方法，该方法融合了LBSN异质网中的用户社交关系、用户-位置签到关系以及兴趣点特征等多维度因素，MRNMF方法既能发现用户模糊社区，又能获得兴趣点聚簇.

上述4种对比方法中，FCM方法代表了典型的模糊聚类社区发现方法；NMF方法是传统的基于对称非负矩阵分解方法发现重叠社区结构；而NMTF和MRNMF方法虽都属于另一种代表性的基于非负矩阵三因子分解的联合聚类方法，但本文的MRNMF方法还通过加入特征项深度融合了多种维度的关系与特征.

4.2 评价指标

实验将采用50次10-折交叉验证法，把表1中2种LBSN数据集上的用户和地理位置随机分为10份，每次选择其中的80%作为训练集，剩下的20%作为测试集，将50次评价结果取平均值得到最终的评估数据.

本文提出的MRNMF模型既能得到用户重叠社区，又能获得兴趣点聚簇.为了评价该结果在朋友与兴趣点上的双重推荐性能，我们采用准确率Precision@K(P@K)和召回率Recall@K(R@K)这2种广泛使用的Top-K指标进行实验比较.另外，为了度量算法的社区划分质量，本文还将模块度作为是一种重要的评价指标，针对重叠社区结构的模块度Q可定义为

(13)

其中，m表示边数，Gij是网络邻接矩阵元素，ki表示节点i的度，Pic表示节点i在社区c中隶属度系数.式(13)表明，模块度Q值越大则表示重叠社区的模块化程度越高.

4.3 实验结果比较

1) POI推荐效果对比

在POI推荐性能方面，本文比较了4种方法在2种数据集上推荐Top-K个兴趣点时的准确率与召回率，结果如图2与图3所示，横轴上的K值表示推荐的Top-K兴趣点数量.由图2与图3可知，在Foursquare(NYC)和Gowalla数据集上，FCM与NMF方法由于仅对单一社交关系聚类而没有用户兴趣点信息，使其基本不具备POI推荐能力，随机推荐实验中的性能指标都低于0.01，因此这2种方法的POI推荐能力可以忽略不计.对于NMTF与MRNMF方法，当设置相同的位置簇数为30时，两者都随着K的增加POI推荐的准确率有所下降，召回率有一定程度的上升.综合来看，本文的MRNMF方法的POI推荐能力显著地强于NMTF方法，其原因是MRNMF方法既考虑用户社交关系和签到关系，又融入了地理位置上的兴趣点特征，在2种数据集上的实验结果都表明MRNMF方法聚类的位置簇结构能有效地促进POI推荐性能的提高.

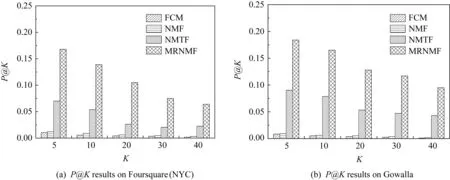
Fig. 2 Precision comparison of POI recommendation图2 POI推荐的准确率对比

Fig. 3 Recall comparison of POI recommendation图3 POI推荐的召回率对比

2) 朋友推荐效果对比

在朋友推荐性能上，本文比较了4种方法在用户层上推荐Top-K个相似用户或朋友的准确率与召回率，结果如图4与图5所示，各方法所设置的用户社区簇参数在Foursquare(NYC)与Gowalla数据集上分别为18与30.从图4与图5可以看出，本文的MRNMF方法在Foursquare(NYC)和Gowalla上对朋友推荐的准确率、召回率指标都普遍优于其他3种方法;FCM与NMF方法有比较相近的朋友推荐性能，原因是这2种方法仅能得到比较简单的用户重叠社区而无法顾及多维关系的影响.在结合了多维关系与特征之后，MRNMF方法比NMTF方法的推荐准确率提升至少25%以上，同时在召回率上高出11%～20%.

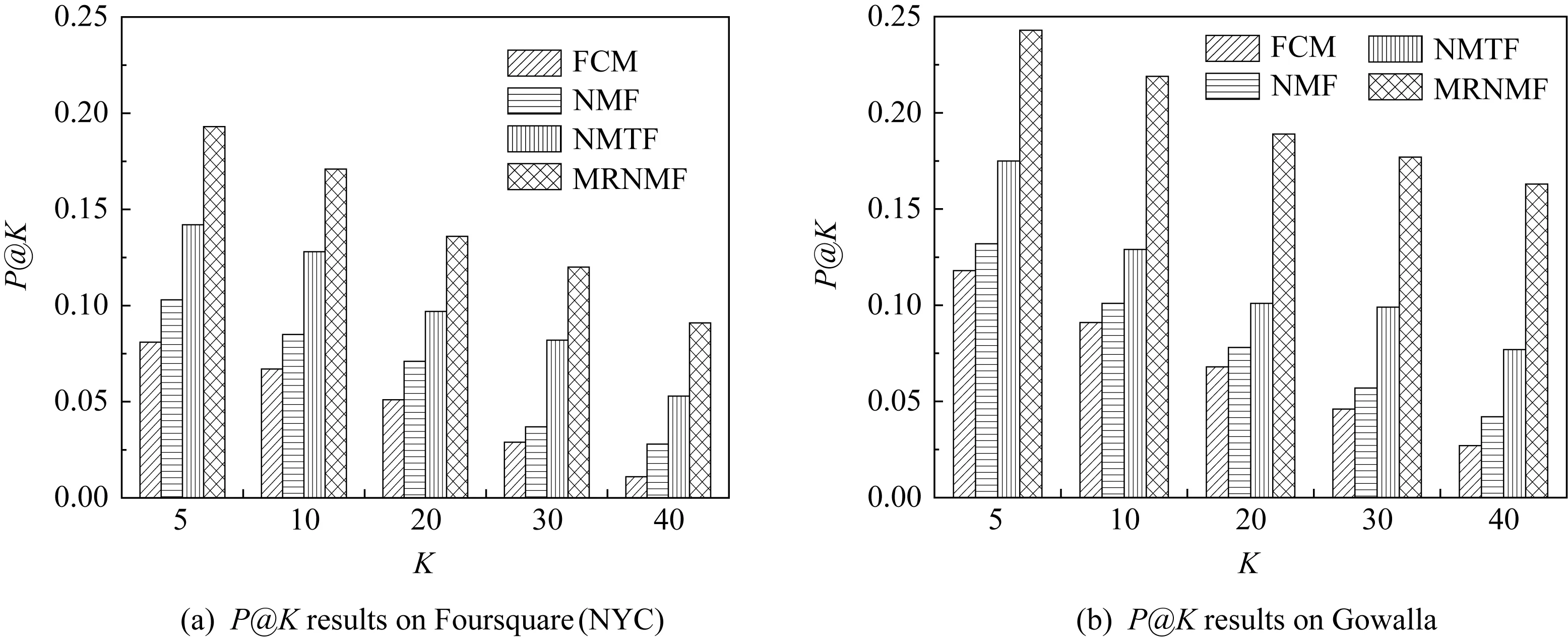
Fig. 4 Precision comparison of friend recommendation图4 朋友推荐的准确率对比

Fig. 5 Recall comparison of friend recommendation图5 朋友推荐的召回率对比

综合图2～5可得出，考虑到地理位置签到密度比用户社交关系存在更大的数据稀疏性，上述 4种方法都在朋友推荐性能上表现出比POI推荐更好的质量；从数据集角度看，4种方法在Gowalla上的朋友推荐性能普遍都比Foursquare(NYC)上的效果更好，这与Gowalla数据集上的用户社交关系较密集有关，用户社区结构特征也更明显.总的来看，本文提出的MRNMF方法既能发现用户重叠社区，又能获得兴趣点聚簇，这两者同时还具有一定的关联性，从而使得该方法在朋友推荐与POI推荐的性能上都整体上优于其他方法.

3) 用户重叠社区的模块度比较

为了评价用户重叠社区结构，本文比较了4种方法分别在Foursquare(NYC)与Gowalla数据集上的重叠社区模块度Q值，设定划分的用户社区簇参数c分别为12，18，24，30，实验结果如表2所示:

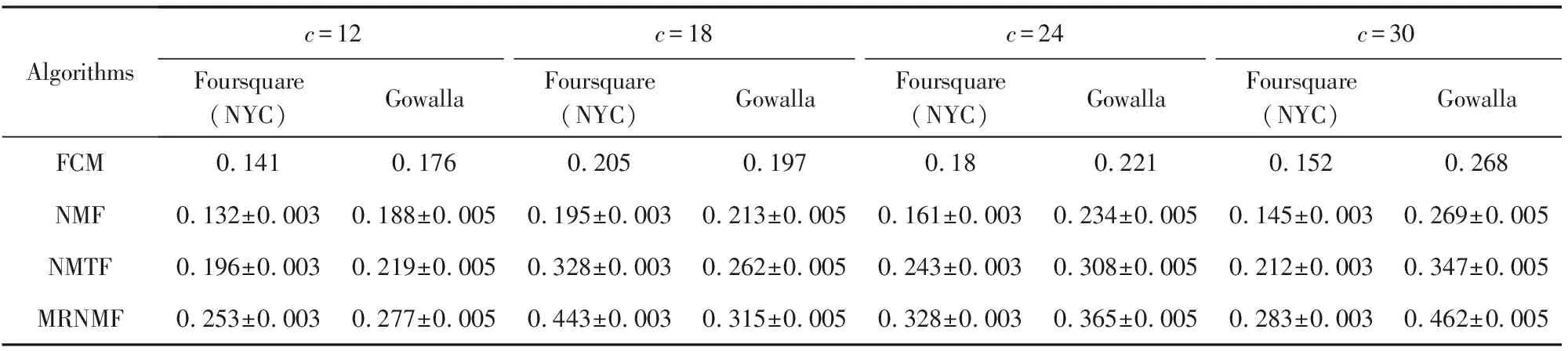
Table 2 Comparisons of Modularity Q Values of Four Methods Under Different Clusters表2 4种方法在不同社区簇c下的模块度Q值对比

从表2中可以看到，FCM与NMF方法在2种数据集上的社区模块度值基本相近，表明这2种方法获得了几乎相同的社区特性，由于两者都仅考虑了单一维度的社交关系，与NMTF与MRNMF方法相比，重叠社区结构仍不够明显.总体而言，本文的MRNMF方法在不同社区簇参数c下都表现出最好的模块度性能，当社区簇大小分别在Foursquare(NYC)与Gowalla上取18与30时有最大的模块度值，其原因是MRNMF方法在矩阵三因子分解中不仅结合了用户社交关系与签到关系信息，还加入了兴趣点特征，因而能够获得最优的用户重叠社区效果，由此表现出最佳的朋友推荐能力.

4) 社区簇c与位置簇g参数的影响分析

下面将考察MRNMF模型中的社区簇与位置簇大小分别对朋友推荐与POI推荐的性能影响.对式(6)进行非负矩阵三因子分解时涉及到2个重要参数是社区簇c与位置簇g，图6显示了社区簇参数分别在Foursquare(NYC)和Gowalla数据集上对朋友推荐的准确率变化情况，而图7则给出了不同位置簇参数在这2种数据集上对POI推荐的准确率结果.

由图6可知，朋友推荐准确率在2种数据集上的变化趋势基本相同，在不同Top-K值下的朋友推荐准确率都随着社区簇的增大而逐渐升高，当用户社区簇c在Foursquare(NYC)与Gowalla上分别为18和30时，推荐准确率达到最大值，这说明划分合适的社区簇有助于发现真实的用户群体.由于数据集Foursquare(NYC)上的用户数量少于Gowalla，且社交用户关系度要比Gowalla的更稀疏，因此在Foursquare(NYC)数据集上的朋友推荐准确率略低于Gowalla.

从图7可以看出，POI推荐在不同Top-K值下的准确率都随着位置簇参数g的增大而平缓升高，当位置簇数在Foursquare(NYC)与Gowalla数据集上分别取35与30时有最好的推荐性能，考虑到地理位置具有较大的稀疏性，并且位置相似性度量受到距离与标签属性因素不平衡的影响，地理位置聚簇的结构特征虽不如用户社区簇那样明显，但比传统POI推荐方法的准确性还是有较大的提高.综上，MRNMF方法能同时获得关联的用户重叠社区与位置簇,有助于提高朋友推荐与POI推荐的精度.

Fig. 6 Effect of community cluster parameter c on friend recommendation图6 社区簇参数c对朋友推荐的影响

Fig. 7 Effect of location cluster parameter g on POI recommendation图7 位置簇参数g对POI推荐的影响

5) 权重因子α与β的影响分析

在如式(6)的MRNMF方法中，α与β分别代表了考虑用户社交关系与兴趣点特征的权重因子，它们在一定程度上调节着用户社区与位置簇的聚类结果.图8与图9分别检验了不同的α与β对Top-K值取10时朋友推荐与POI推荐的准确率变化情况.在2种数据集上的实验结果显示，参数α与β分别对朋友推荐与POI推荐的准确率表现出基本相同的变化趋势，即都是先升后降的过程，并各自在0.5与0.1时取得最大值.实验验证了α与β所控制的社交关系与兴趣点特征比重能够直接影响到朋友推荐与POI推荐的效果.

Fig. 8 Precision results of friend recommendation influenced by parameter α图8 参数α对朋友推荐的准确率影响

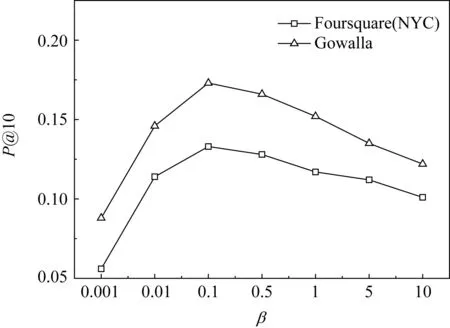
Fig. 9 Precision results of POI recommendation influenced by parameter β图9 参数β对POI推荐的准确率影响

5 总 结

异质网络中的社区结构是当前非常值得关注的研究方向，现有研究一直都面临着如何融合多模实体及其多维关系的挑战性难题.本文针对LBSN这种新型异质网络中的社区发现问题，提出了一种融合用户与位置实体及其多维关系的社区发现方法MRNMF.该方法采用基于非负矩阵分解的联合聚类模型，通过构建基于距离度量的损失函数来评估矩阵近似分解误差，并在此基础上考虑结合用户社交关系、用户-位置签到关系以及兴趣点特征等多维度的影响因素，使之融合到统一的表示模型中，然后运用随机梯度下降法来求解目标函数的局部最优值.其最大的优势和创新点是通过基于NMF的联合聚类方法能同时获得LBSN中紧密关联的用户模糊社区与兴趣点聚簇，以有效缓解推荐中的数据稀疏问题.最后，在Foursquare(NYC)和Gowalla数据集上的实验结果表明，本文所提的MRNMF方法在准确率和召回率2个评价指标都优于其他传统的社区发现方法，在朋友与兴趣点这双重推荐上都具有最优的推荐性能.在未来工作中，我们将进一步考虑时间因素挖掘出反映用户及兴趣点迁移的社区演化结构.