分布式深度学习框架下基于性能感知的DBS-SGD算法
纪泽宇 张兴军 付 哲 高柏松 李靖波
(西安交通大学计算机科学与技术学院 西安 710049)
在过去10年间,深度学习[1-2](deep learning, DL)算法在图像分类、语音识别、自然语言处理以及无人驾驶等领域得到了广泛应用并产生了巨大的影响[3-5],这在很大程度上归功于更深层次的神经网络模型以及相对海量的训练数据.然而,复杂的网络模型和海量的训练数据大大提高了神经网络的训练开销.
由于大规模深度神经网络训练受制于有限计算资源,研究人员进行了诸多利用分布式计算框架加速神经网络训练的工作.例如:Dean等人[6]以及Chilimbi等人[7]分别建立了1个集成多个商用CPU的集群,并在此之上对数据进行并行训练;Seide等人[8]以及Strom[9]均使用由集成多个GPU的节点构成的异构计算平台进行并行加速;Gupta等人[10]使用高性能计算集群进行训练等.
为了使神经网络算法能够在分布式计算框架下运行,研究人员通常会采用相应的并行模型.目前流行的深度神经网络并行模型主要分为2种:模型并行(model parallelism)[11]和数据并行(data parallelism)[12].

Fig. 2 Data parallelism图2 数据并行
在大多数情况下,模型并行所带来的通信和同步开销远远超过数据并行,加速比较低,因此目前大多数的研究工作都集中在数据并行领域.随机梯度下降(stochastic gradient descent, SGD)算法[14]具有实现简单、收敛速度快、运行效率高等诸多优点,因此在深度神经网络算法中得到了广泛的应用.深度学习分布式策略可以分为基于参数分布形式的研究以及基于模型一致性的研究.参数分布形式研究包括去中心化[15-16]和中心化[6,17-18]2类.在去中心化的方法中,每个工作节点都维护1个本地的参数并根据指定的通信图进行参数传递和更新.在中心化的方法中,由被称为参数服务器[17]的中央节点维护全局参数,而其余的工作节点进行计算工作.而基于模型一致性的研究则包含了同步更新模型[11,19-20]、异步更新模型[6,21]和过时同步更新模型[10,22].在同步更新模型中SSGD(synchronization-SGD, SSGD)算法是基于SGD算法最简单直接的分布式实现,最早是由Langford等人[19]提出.在该算法中,主机简单地将数据划分并映射到相应的工作节点上,通过使用显示栅栏进行强制同步,能够确保主机各工作节点都使用相同的模型参数来进行梯度计算,然而各节点在每次迭代中会被强制要求等待其中工作最慢的节点.这种同步策略所付出的代价是降低了SSGD算法的可扩展性以及运行时性能.为了解决这个问题,Zheng等人[21]提出了基于异步更新模型的ASGD(asynchronization-SGD, ASGD)算法,该算法通过消除各节点间的同步栅栏来克服上述缺点.然而这种异步行为又不可避免地给整个系统引入了“梯度过时”:由于计算梯度是需要时间的,因此当某个节点计算完梯度值并提交给服务器更新参数时,全局参数可能已经被更新了数次,那么此次更新的参数就会存在一定的过时量,因而不是最新的收敛方向,这种现象被称为“梯度过时”.因此在确定迭代次数的前提下,ASGD训练的模型往往比SSGD训练的模型效果差很多,严重的梯度值过时会明显减慢网络模型的收敛速度,甚至完全停止收敛.而过时同步更新模型[22]则是在同步更新模型与异步更新模型之间做权衡,当运行快的工作节点在达到一定梯度过时量时将被强制进行全局同步操作,从而缓解梯度过时问题带来的影响.
目前有很多针对异步梯度下降算法中出现的梯度过时问题的研究[6,22-24],其中大多数异步随机梯度下降算法的基本思路大致相同,主要差异是采用了不同的优化策略来减少过时梯度所造成的影响.Dean等人[6,22]在参数服务器端使用了延时同步技术,每隔一定迭代轮数,服务器将进行1次强制同步,从而消除梯度过时的影响.Zhang等人[23]提出了一种ASGD算法的变体,该算法根据不同时刻的梯度过时值动态调整学习速率,同时具有很强的收敛性.Chen等人[24]提出在每次训练时多使用5%~10%的节点,以随时替换那些性能较慢的节点,从而尽可能保证系统中所有节点性能的一致性.虽然这些研究通过不同的方式消除了梯度过时带来的影响,但是相关算法均运行在各节点性能较为平均的同构平台上,没有充分考虑到商业级云计算环境.Jiang等人[25]提到了商业级云计算平台中3种典型的应用场景:
1) 网络和计算异质性.在1个由不同数据中心提供的数千台商用机器组成的集群中,各机器很难保证拥有同代处理器,这样就使节点间的性能存在差异.
2) 资源竞争.在1个面向多用户的集群中,通常需要同时处理多个应用请求,那么这些请求将不可避免地在同一个节点上竞争稀缺的硬件资源.因此1个应用的不同实例通常具有不同的运行时间.
3) Spot Instance.Amazon EC2通过使用Spot Instance来为用户提供服务.为了大量节省成本,不同资源需求的实例能够运行在同一个集群上(例如m4.large具有2个核,a1.4xlarge具有16个核).那么当1个用户在这样的集群上提交任务时,与被分配了高性能硬件的工作节点相比,被分配了低性能硬件的工作节点需要花费更多的时间计算等量的数据.
这3种应用场景导致不同节点提供的算力各不相同,此时节点间计算性能的差异导致了梯度过时问题的产生.基于异质性环境中的计算性能差异问题,Jiang等人[25]通过测试发现SSP模型策略在异质性集群上的运行时间比正常慢了约80%,同时在SSP模型的基础上动态优化学习率以解决异质性带来的问题,而Luo等人[16]则基于去中心化的研究并结合Chen等人[24]提出的backup works方法来解决异质问题.本文针对异质性的分布式运行环境提出了一种基于性能感知技术的动态批大小(batch size)随机梯度下降算法(dynamic batch size SGD, DBS-SGD),该算法可以有效地根据各节点间不同的性能,合理地分配与之相适应的数据量,最终使得各节点在异步更新的情况下达到基本相同的迭代次数,从而消除由性能差异引起的梯度过时问题带来的影响.
本文主要工作有2个方面:
1) 提出了一种可以快速量化各节点性能的模型.此模型通过对节点最近N次运行时间进行统计和计算,对节点当前性能进行量化,以方便对各节点性能进行直接评估.
2) 基于上述的节点性能量化模型,提出了一种基于性能感知技术的动态batch size随机梯度下降算法DBS-SGD.在得到各节点性能的量化值后,该算法能够实时地调配各节点的工作量,使得各节点每次迭代的运行时间基本一致,从而解决了由性能差异引起的梯度过时问题,消除了梯度过时对系统的影响.
1 神经网络及分布式框架
本节我们将对分布式深度学习的相关理论、参数服务器整体框架及分布式系统中的同步策略进行分析.
1.1 深度学习算法
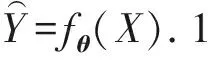
(1)
其中,εn表示数据集中第n个数据,w为整个神经网络的参数,f(w,εn)表示使用了参数w和εn的复合损失函数.
神经网络模型采用反向传播算法对网络中的各参数进行求导并依次更新,每次迭代对参数进行更新的表达式为

(2)

(3)

由于梯度下降算法需要在整个数据集上进行计算,其计算时间较长,同时比较容易陷入局部最优解.因此出现了很多关于梯度下降的变种算法,如随机梯度下降算法、批量梯度下降算法等.随机梯度下降算法和小批量梯度下降算法的表达式为

(4)

(5)
1) 随机梯度下降算法.每1次只选取1个数据进行梯度的计算,然后进行迭代.
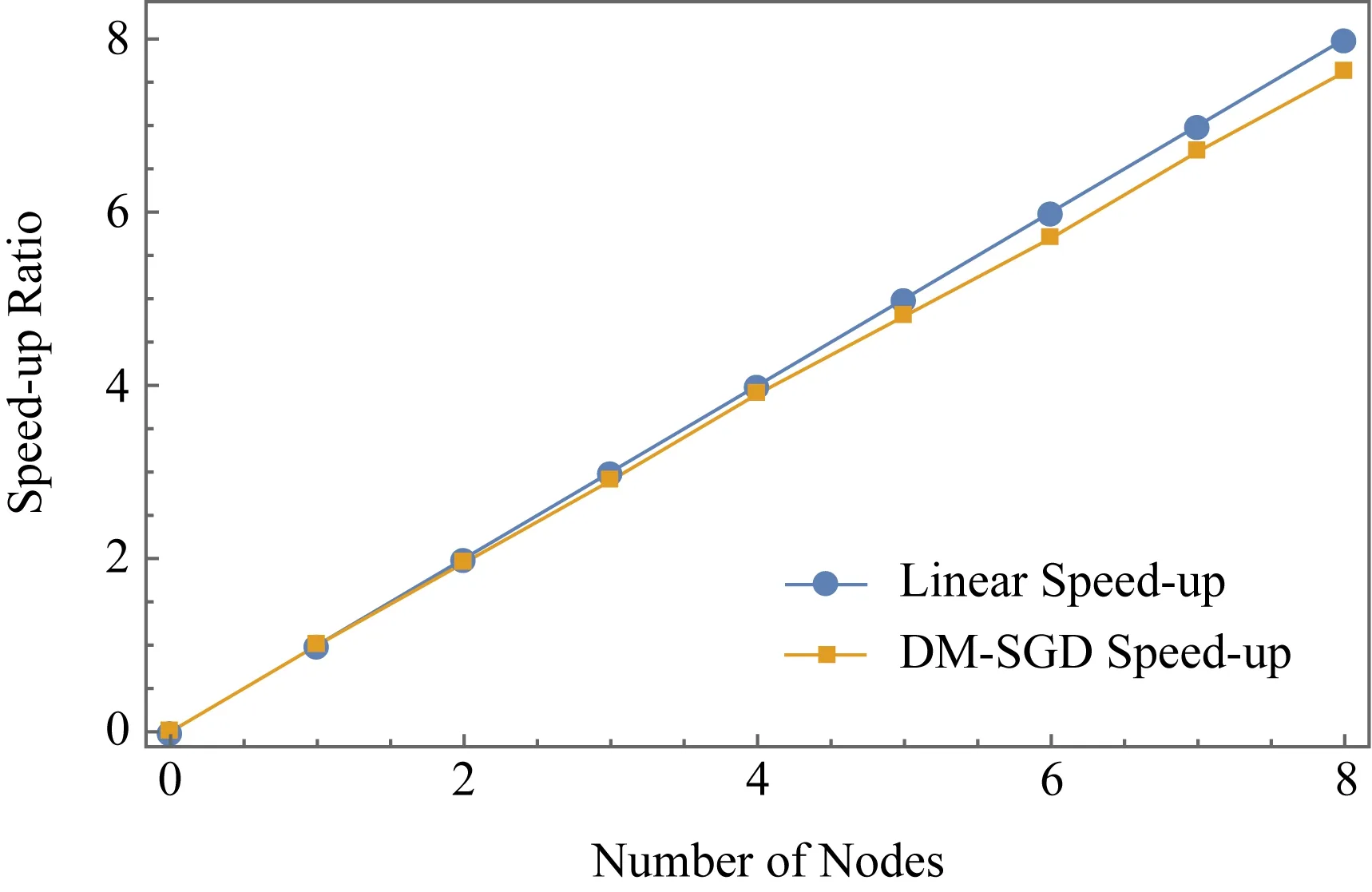
2) 小批量梯度下降算法(mini batch gradient descent, MBGD).它是对梯度下降算法和随机梯度下降算法的折中,取k个数据进行梯度的计算,1 在集群环境中,参数服务器架构[17](如图3所示)是目前主流的支持分布式并行深度学习的架构,其最早原型为谷歌团队开发的Distbelief[6],是大规模深度学习在不断使用过程中抽象出来的架构. Fig. 3 Parameter server framework图3 参数服务器架构 在此架构中,工作节点相关参数及操作定义如下. 1)λ.工作节点个数. 2)μ.每个工作节点在计算梯度时所用minibatch的大小. 3)η.学习率,也称为步长. 4) 时间戳.使用标量时钟的计数值来表示梯度权重时间戳i,从i=0开始.每次权重更新将会使相应时间戳的值增加1,梯度的时间戳与权重的时间戳相同. 5)τi,l.工作节点l的梯度过时值.1个工作节点将带有时间戳j的梯度值发送到带有时间戳i的参数服务器上,i≥j.以i-j的形式来计算梯度的过时量τi,l,对于任意的i和l,τi,l≥0. 每个工作节点顺序的执行操作有4个: 1) getMiniatch.从训练集中随机选择1份小批量的样本. 2) pullWeights.向参数服务器发出请求,申请当前的参数集. 3) calcGradient.根据选择的小批量样本产生的训练误差来计算梯度值. 4) pushGradient.将计算好的梯度发送给参数服务器. 参数服务器对模型的全体参数进行统一维护并执行2个操作: 1) sumGradients.接收各工作节点计算好的梯度值并进行累加操作. 2) applyUpdate.用计算好的梯度值乘以学习率并更新全局的参数. 在服务器端,可以使用不同的更新策略,包括同步更新策略和异步更新策略.同步更新策略也可被称为硬同步策略(synchronous-SGD),异步更新策略称也可被称为软同步策略(asynchronous-SGD).第2节将会讨论不同更新策略对梯度产生的不同影响. SSGD是梯度下降算法在分布式系统上最直观的实现,该算法在服务端采用参数平均法[26]来处理权重的更新值,同时可证明分布式环境下的SSGD算法能够在数学上完全等同于单机环境中的该算法,证明过程见附录A.由附录A中式(A1)(A2)可知:参数服务器端通过聚合各节点在第i步计算完成后提交的各梯度变化值来更新第i+1步的权重,从而保证第i步产生的梯度过时量为0,即没有梯度过时问题,因此这种算法会生成具有最佳准确度的模型. 通过每次迭代进行强制同步来保证参数更新的一致性,在工作节点较少时,该算法扩展性表现较好,但是在大规模集群中,强制同步的机制会造成木桶效应从而使整个系统的效率变得很低,如图4所示: Fig. 4 Synchronous method图4 同步更新策略 为了解决上述问题,软同步策略提出将参数计算的过程从参数服务器端转移到节点端,参数的更新就会变成: (6) (7) 当服务器端依旧采用同步方式更新参数时,该方法完全等价于参数平均法.然而服务器放松同步约束后,当服务器接收到任意1个节点计算得到的新参数时就立刻进行更新全局参数的操作,而非等待所有节点的计算结果.该策略就变成了ASGD算法,如图5所示.ASGD算法有2个主要的优势: 1) 增加了整个分布式系统的数据吞吐量,各工作节点可以把更多的时间投入到计算中,而非等待其他节点; 2) 相比于同步更新方式,各节点可以更快得到其他节点的信息(参数更新值). Fig. 5 Asynchronous method图5 异步更新策略 Fig. 6 The process of updating global parameter图6 全局参数更新过程 异步更新策略在获得以上优势的同时也带来了新的开销.当全局参数采用异步更新策略时,梯度过时问题也随之而来.因为计算梯度本身是需要消耗时间的,所以当某个节点计算完梯度值向参数服务器提交时,参数服务器端维护的全局参数可能已经被更新了多次,具体流程如图6所示. 从图6中展示的参数更新流程可以看到,w101的值是基于w97计算得到的,而非最近的w100的值.2个权重的下标之差大于1,这意味着梯度的更新不是基于最新的参数,于是产生了梯度过时.Gupta等人[10]论述了此模型下梯度的最小平均过时值为工作节点的数量n,事实上由于各节点的迭代时钟周期数不同,梯度过时的值一般大于n,同时由于系统中节点数量的增加以及节点间性能差异的增大,梯度过时问题更加严重. (8) (9) (10) Fig. 7 The top-k method图7 top-k更新策略 这种更新策略能较好地解决异步更新策略所引发的梯度过时问题,但仅适用于各工作节点性能较为平均的情况下.第2节将会对不同策略的梯度过时问题进行量化分析. 在第1节中提到的SSGD算法采用了显式的同步栅栏,在每一步向前迭代的过程中,参数服务器会做一个强制的聚合运算,因此每个工作节点从服务器端得到的参数都是最新的,即梯度过时值为0.但是当更新策略变为异步更新时,不可避免地引入了梯度过时问题.为了解决这个问题,首先要对梯度过时产生的原因进行分析. 假设参数服务器系统中有30个工作节点即λ=30,那么对于1-soft更新策略,参数服务器需要收集30次来自工作节点的梯度值,然后再进行参数的归约和更新操作.同样地,对于2-soft更新策略,参数服务器需要收集302=15次来自工作节点的梯度值后再进行参数更新.根据Zhang等人[23]和Gupta等人[10]的工作,对于系统中的每个工作节点,无论其batch_size的大小和训练模型的大小如何变化,均可得到图8相似的经验性实验结果.从图8(a)看到,对1-soft更新策略来说,梯度过时值为0,1,2,对于图8(b)中的15-soft更新策略,平均的梯度过时值变为0~30.如果是30-soft同步策略,那么参数服务器从任意工作节点收到计算结果后即对参数进行更新操作,这时等价于ASGD算法,该算法下梯度的过时值为0~60,并呈高斯分布.可以看出在ASGD算法中,工作节点数量的增加导致了梯度过时值的增加.从图8(a)(b)中可以看到,对于n-soft策略来说,平均的梯度过时值接近于n.这是基于各工作节点性能完全一致的情况下得到的结果.如果各工作节点的性能差异性较大,那么该算法下产生的平均梯度过时值就会变大,而且梯度过时值变化会从较为稳定的高斯分布变成1个随机性更大的分布.如图9(a)(b)所示,梯度值在n附近的概率下降,同时原本2侧发生概率较低的地方,它们发生的概率反而得到了上升.这会导致损失函数在收敛的过程中出现剧烈的抖动,从而影响最终的收敛效率和结果.DBM-SGD算法的思想就是根据各节点的实时性能动态地分配给各节点不同的工作量,即batch_size的值,通过这样的操作,使得各节点每个迭代的时间基本一致,那么在这种情况下,整个系统梯度过时值的分布情况将再次回归到正常的高斯模型上,平均的梯度过时量减少到n,趋向稳定,最终收敛恢复正常. Fig. 8 Gradient distribution with 2-soft synchronous and 15-soft synchronous图8 采用2-soft和15-soft策略的梯度分布 Fig. 9 Gradient distribution with 2-soft and 15-soft(different performance)图9 采用2-soft和15-soft策略的梯度分布(节点性能不一致) 在之前的研究[14,16,22-23]中,batch_size的值m通常设置为固定值,因此各节点训练的数据量是一样的,m一般是临时选择或通过经验测试选择.Balles等人[27]提出在神经网络训练的过程中动态地调整batch_size的值可以加速算法的收敛,这就说明batch_size的值实际上是1个关键变量,它的变化会对神经网络性能产生错综复杂的影响.一方面,随机梯度的方差(即收敛程度)随m的取值线性减小,那么较大的批量值能够得到较具体的梯度信息,从而减少了整体的收敛步骤数;另一方面,每次迭代的计算成本随m的取值线性增加,因此可以线性地权衡方差和时间成本.从随机梯度下降算法每次更新参数的公式中可以看出,随机梯度下降算法每次迭代只使用从1个样本数据计算出的值进行参数更新,而梯度下降算法使用全部数据计算的值进行更新.Nemirovski等人[28]从数学上证明了两者的最终收敛趋势是一致的.不同的是使用了全部样本进行更新的梯度下降算法每次收敛的方向是最优的(梯度最陡),而使用1个样本数据的随机梯度下降算法每次收敛的方向有较大的波动.因为不是走的最优路径,所以这种抖动的结果一方面会导致函数总体迭代次数的增加,另一方面使函数有很大的概率跳出局部最优的区域,从而找到更好的解. 而mini batch SGD算法则对各节点batch_size的值进行了折中(1 根据分析,可以得出的结论为: 在每次神经网络训练的迭代中,训练数据的大小,即batch_size的值决定了这次迭代收敛方向的准确率.batch_size的值越小,收敛的波动性越大,如果batch_size=1,等价于SGD算法.batch_size的值越大,其收敛的方向越准确,如果batch_size的值为n,等价于GD算法.因此在每次迭代的过程中动态地去调整batch_size的值(无论是分布式还是单机)并不会影响整体的收敛趋势. 结合2.2节对batch_size取值的分析,在采用处理器作为计算资源的集群中,性能感知模型可通过分析节点的工作状态预测并得到节点当前的性能数据.在单个节点中影响程序运行的因素有很多,包括硬件架构、操作系统、编译环境、编程框架、算法等.模型中涉及的参数越多,其预测的结果越准确,但同时采集数据带来的开销也将增大.首先本模型的目标是实时地预测工作节点运行效率,因此应优先考虑数据的时效性;其次在异质性的应用场景中,其底层的硬件架构往往不同,因此数据采集的开销也随之增大.可见,性能感知模型中选取的参数应兼具时效性和易取性.对于单个节点的性能评估主要有较为直观的参数进行表示:迭代次数、运行时间.而梯度过时出现的主要原因是节点数量过多以及节点间的计算性能不一致,使得节点进行参数更新的时间出现间隔,本文主要的应用场景为后一种情况.为了尽可能减少梯度过时带来的影响,应该保证各节点每次迭代的时间一致,而非最终的迭代次数一致,同时运行时间易获取且能够较为直观地反映该节点当前的运行效率,所以选择以节点迭代1次所运行的时间为量化标准更为合理.从第N轮次的迭代开始(即最初运行时不计算其平均运行时间),之后每轮迭代取该节点最近N次的平均运行时间(经多次试验结果分析,N的值设置为5~10时统计效果较好.)作为各节点当前的性能指标,以此来对所有的节点进行计算性能的量化评估. 结合上述的性能感知模型,DBS-SGD算法进行的操作为:各节点使用1组长度为N的向量来保存本地节点的工作状态,向量保存本地节点最近N次迭代的运行时间序列,每轮迭代完成后将最新1轮的运行时间加入向量以替换最旧1轮的运行时间.如果本地节点为基准节点,那么在统计自身最近N次迭代运行时间的同时还需要将此值发送至服务器端,通过服务器将基准的运行时间广播给其他工作节点.在深度学习算法中,节点每次计算1个实例过程的计算量是一样的,因此每轮迭代所使用的时间与训练的数据量成正比关系.算法中以0号节点作为基准,本地节点每次迭代都与0号节点的最近N轮平均运行时间进行对比,若该比例落在一定范围内,则说明该节点的性能与基准节点相似,它的batch_size不需要进行调整,否则需要对该节点的batch_size进行等比例的放大或缩小.通过算法的调度,整个系统中所有节点的运行时间都和0号节点的运行时间大致保持在同一个层次,最终避免了由于节点间性能差异过大而引发的梯度过时问题.该算法还需要在参数服务器端新增加1个1维向量来保存0号节点的运行时间.因为每轮迭代的运行时间这个参数较为直观,对其获取和统计很方便,很容易保证其时效性,同时对节点进行量化的计算操作也并不复杂,所以即便在每次迭代中都需要进行性能量化,所增加的计算开销相对于深度学习本身的计算过程来说也可以忽略不计.基于这些理论和模型,可以得到算法1. 算法1.DMB-SGD工作节点端算法. 输入:当前节点的最近m次的CPU时钟计数; 输出:下一轮当前节点要使用的batch_size值. ① 从服务器端接收最新的全局参数以及0号节点最近m次的计算时间; ② FOR 迭代次数i=1,2,…,N ③S=sum(0号节点最近m次的计算时间)sum(当前节点最近m次的计算时间); ④ IF当前节点不为0号节点 ⑤ IF |1-S|≥A ⑥batch_size=X×S; ⑦ ELSE ⑧batch_size不变; ⑨ END IF ⑩ ELSE 算法2.DMB-SGD服务器端算法. ① WHILE TRUE DO ② IF收到0号工作节点之外的请求 ③ 发送0号节点最近m次迭代时间,并发送最近一次更新的全局参数; ④ END IF ⑤ IF收到0号节点的信息 ⑥ 将0号节点最新一次迭代的时间入栈,将最近的第m+1次数据出栈,并发送最近一次更新的全局参数; ⑦ END IF ⑧ END WHILE 注:X和m的值需要经过实验给定比较优的值,并不是越小或者越大越好.A为1个常量. 在理想情况下,该算法可以使各节点产生1个隐式的栅栏,在显式同步栅栏的约束下接近或达到同步更新的效果. 为了测试该算法的效率,本文分别评估了单机运行并使用ASGD模型以及经过算法优化后的方法在Mnist和cifar10 benchmark上的效率. 实验的测试环境为:Intel®CoreTMi7-6700 CPU核心频率3.40 GHz,内存8 GB.实验用的软件为tenserflow1.6-CPU版.为了模拟性能差异较大的分布式运行环境,本实验采用了容器的机制,通过-c--cpu-share或者--cpus来限制容器能使用的CPU资源或者CPU核数.在实验测试中,分别模拟了4节点和8节点的分布式训练场景,为了模拟异质性环境,一半的节点CPU配置为1个CPU负载(docker配置参数为--cpus=1),另一半的节点CPU配置为1.5倍CPU负载(docker配置参数为--cpus=1.5),表示前一半节点的CPU负载为后一半节点的约70%.内存配置为各容器平均分配5 GB内存.容器系统默认为每个容器创建1个唯一的IPC命名空间,在默认情况下容器之间无共享内存,实验中为了更真实模拟分布式环境,也没有使用共享内存机制. Mnist(mixed National Institute of Standards and Technology)数据集来自美国国家标准与技术研究所,它是手写体数据集,是1个非常通用的进行分类测试的通用数据集,其包括1个训练图片集、1个训练标签集、1个测试图片集和1个测试标签集,其中训练数据由5万张28×28像素的手写体数字图片组成,测试数据包含10 000张图片. cifar10数据集共有60 000张彩色图像,这些图像是32×32的像素,分为10个类,每类6 000张图片.每类中的50 000张用于训练,构成了5个训练批,每一批10 000张图片;另外10 000张用于测试,单独构成1批.测试批的数据里,取自10类中的每一类,每一类随机取1 000张.抽取后剩下的随机排列组成了训练批.1个训练批中的各类图像并不一定数量相同,总的来看训练批,每一类都有5 000张图.需要说明的是,这10类都是各自独立的,不会出现重叠. 对于Mnist数据集,构建了全相接的神经网络,其中包括2个隐藏层和1个输出层,隐藏层包含了200个神经元,输出层是1个10路的输出函数softmax(),该函数在10个输出类上生成了相应的概率分布,学习率设置为0.001,并对损失函数进行优化,优化函数为adamoptimizer().对于batch_size的设置,设置为256.每个工作节点按访问顺序从数据集中顺序地读取batch_size个数据作为子数据集. 对于cifar10数据集,首先对原始数据进行了预处理,将32×32的图片重新从中心取24×24的尺寸,再进行反转、调整亮度、对比度等操作,增加数据集的容量,以保证更好的学习效果.随后同样采用LeNet卷积神经网络,有2个卷积层,每个卷积层接1个池化层,其中每个卷积层卷积核的大小为5,核数为32,池化层的核尺寸为2,步长为2,采用的方式是取区域最大值,随后全相连的2层神经网络,包含128个神经元,输出层1个10路的输出函数softmax(),该函数在10个输出类上生成了概率分布,学习率设置为0.000 1,并对损失函数进行优化,优化函数为adamoptimizer().对于batch_size的设置,类似于Mnist数据集,只是每个工作节点按照顺序从数据集中随机地读取batch_size个数据作为子数据集. Mnist数据集大小约为55 MB(压缩后约为11 MB),cifar10数据集约为180 MB(压缩后约为140 MB),同时LeNet模型包含约6万个参数,数据大小约为240 KB.分配给docker的内存空间远大于数据集和网络模型所需的存储空间,训练的全过程都可以在内存中进行,因此不存在内存与硬盘之间数据访问的延迟. 节点间的模拟网络是1个2层交换网络,其网络延迟在0.04~0.08 μs之间.同时神经网络1次迭代的计算时间至少需要0.15 s(实验时对2个数据集均采用LeNet模型),因此容器间由于网络通信而造成的开销相对于计算来说是可以忽略不计的. 首先对性能预测模型进行测试,在节点上对于Mnist数据集使用了全相联神经网络和LeNet网络进行测试,对于cifar10数据集采取LeNet网络进行测试,测试结果如表1所示.在cifar数据集上,设置迭代次数为1 000,可以看到程序的运行时间与batch_size的取值呈线性关系,且batch_size的值翻倍,程序运行时间也随之翻倍,同样的现象Mnist数据集上也可以观测到.Mnist数据集上,当使用全相联网络测试,迭代次数设置为1 000时的测试结果不是很准确.造成这个现象的原因是由于Mnist数据集为黑白图片,同时使用了结构较为简单的2层全相联神经网络,与卷积神经网络(convolutional neural network, CNN)网络相比,其计算量相对较小,最后设置的迭代次数量级也较低,所以程序的运行时间很短,结果不稳定.当其迭代次数设置为2 000之后,可以看到结果已经恢复正常.此测试结果与之前性能预测模型的理论分析相符. Table 1 Test on Performance Predict Model表1 性能分析模型测试结果 Fig. 10 Value of loss function on Mnist图10 Mnist数据集loss函数值整体下降趋势 图10~13中使用的数据集为Mnist,是在4个节点的情况下使用ASGD算法、SSGD算法和n-soft与本算法进行对比,其中n-soft算法中参数设置为2,即服务器每收到2个节点的更新值更新1次全局参数,而基于同步更新策略的SSGD算法,其梯度过时量为0,作为基准参考以测试其余算法最终的收敛精度.4个算法中batch_size的值设置为400,均使用LeNet模型进行训练.在图10,11中,ASGD-0.78表示在4个节点中性能最低的节点和性能最高的节点进行性能量化后的百分比为78%.图10中可以看到经过本算法优化后,在相同迭代步数内,其收敛速度更快,快于ASGD算法和n-soft算法,略低于SSGD.图11中可以看到经过算法优化,loss函数值在相同迭代次数下降低了60%.图13中可以看出在异质性环境中,经算法优化后,神经网络模型的精度收敛曲线最陡并在更少的迭代步数内达到了最优,收敛趋势接近基于同步策略的SSGD算法.图12中则展示该算法在扩展到8个节点时所达到的加速比. Fig. 11 Value of loss function decreased by about 60% on Mnist图11 Mnist数据集loss函数值下降约60% Fig. 12 Speed-up on Mnist图12 Mnist数据集算法的扩展性 Fig. 13 Accuracy on Mnist图13 Mnist数据集上分类精度的收敛趋势 对于cifar数据集,同样做了与ASGD算法、SSGD算法以及n-soft算法的对比测试,其中n-soft算法中参数设置为2,即服务器每收到任意2个节点的更新值更新1次全局参数.同Mnist数据集的实验一样,也以基于同步策略的SSGD算法作为衡量基准以测试其余算法最终的收敛精度.4个算法中batch_size的值设置为400,均使用LeNet模型进行训练.从图14中可以看出,在4个工作节点的情况下,节点间性能差异越大,收敛过程中抖动的情况出现得就越频繁,抖动幅度就越大,这种情况出现的原因已经在第2节中进行了分析.严重的梯度过时问题导致了收敛过程中出现频繁的抖动,并影响最终的收敛精度.而经过算法优化后,神经网络的收敛过程就显得较为平稳,收敛精度也提高了10%,其效果优于ASGD算法和n-soft算法,略低于基于同步策略的SSGD算法.图15中同样可以看出在异质环境中,经算法优化后神经网络的loss函数值也有10%的下降,其收敛趋势同样快于ASGD算法和n-soft算法,接近基于同步策略SSGD算法的收敛曲线.在图16中,展示了算法扩展到8个节点时所达到的加速比,接近线性加速. Fig. 14 Accuracy on cifar10 after 10 000 iterations图14 cifar数据集10 000次迭代算法达到的准确率 Fig. 15 Value of loss function on cifar10 after 10 000 iterations图15 cifar数据集10 000次迭代算法达到的loss函数值 Fig. 16 Speed-up on cifar10图16 cifar数据集算法的扩展性 对于使用该算法所产生的的开销,在第2节进行了描述,仅在每次节点与参数服务器端进行通信的时候多传输了1组关于0号节点最近m次迭代时间的向量,其数据量的大小相对于全局参数来说不到1%.同时在工作节点上进行动态batch_size的计算量相对于深度神经网络算法的计算量同样不到1%.因此该算法所产生的开销非常小,可以忽略不计,在2个数据集上进行的测试结果也说明了这一点.Mnist数据集使用的图片尺寸很小,进行分类的神经网络结构也比较简单.在数据集和计算量都不大的情况下,该算法依然可以达到近似线性的加速,说明了算法产生的开销对整体的收敛影响很小.对于数据集较大的cifar10以及更复杂的卷积神经网络来,该算法产生的开销占比会更小,从而不会影响算法的收敛. 从实验中可看出:同异步梯度下降算法以及n-soft算法相比,算法都去掉了等待时间,充分利用了全部的计算资源,但是本算法通过合理的任务分配,减少了梯度过时的影响,因此可以看到在相同的时间内收敛得更快,性能更好. 为了解决深度学习数据并行过程中产生的梯度过时问题,本文设计的性能分析模型解决了分布式系统下各节点性能不易量化的问题.同时本文根据该模型提出了基于性能感知的DBS -SGD算法并从理论上证明了算法的收敛性.该算法通过性能感知模型实时检测各工作节点的计算性能,并为计算性能不同的工作节点动态分配相应工作量,从而解决了梯度过时问题,使神经网络收敛速度加快.实验结果表明,该算法使得分布式系统中各节点的单次迭代时间达到一致,解决了梯度过时问题.与传统的ASGD算法以及改进的n-soft算法相比,本文提出的DBS-SGD算法在相同的迭代次数下神经网络的收敛速度更快,同时该算法能够获得接近线性的加速比. 未来的工作包括2个方向:1)如何为各节点的不等量任务分配相应的权值,以更好地量化各节点在每次提交梯度更新时所做出的贡献;2)结合第1个研究方向将本算法应用在同步更新策略上,可以使神经网络收敛的次数达到理论上的最低.1.2 参数服务器

1.3 服务器参数更新策略


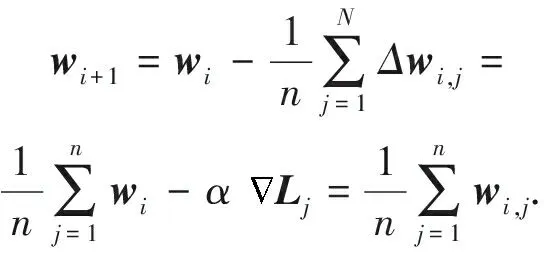







2 性能感知模型与DBS-SGD算法设计
2.1 节点性能不一致情况下的梯度过时分析


2.2 batch_size对梯度下降算法的影响
2.3 性能感知模型及DBS-SGD算法
3 实验结果与分析
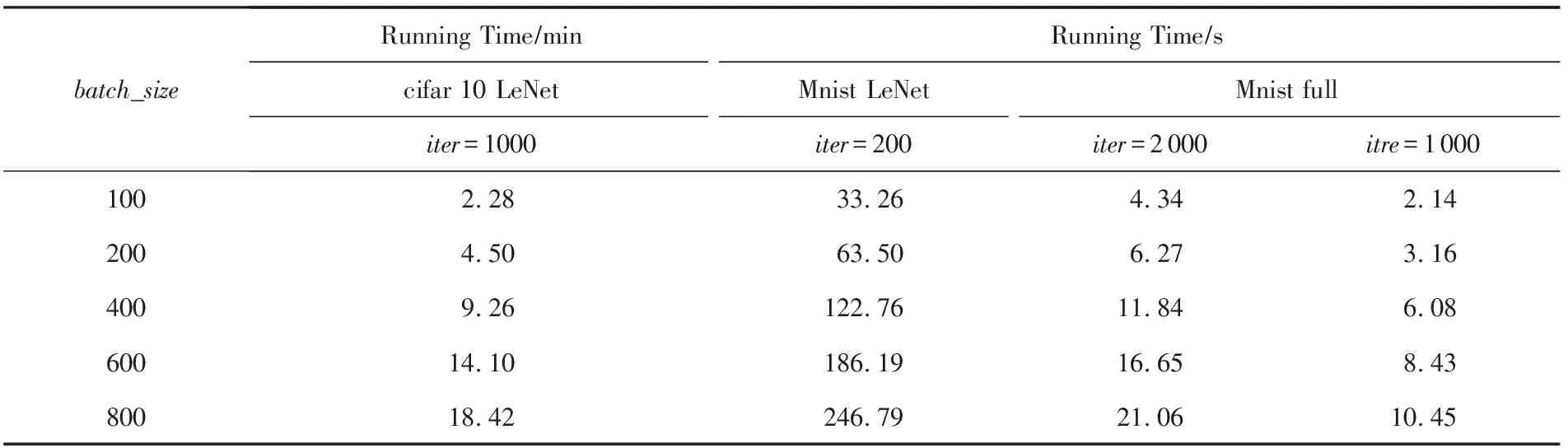




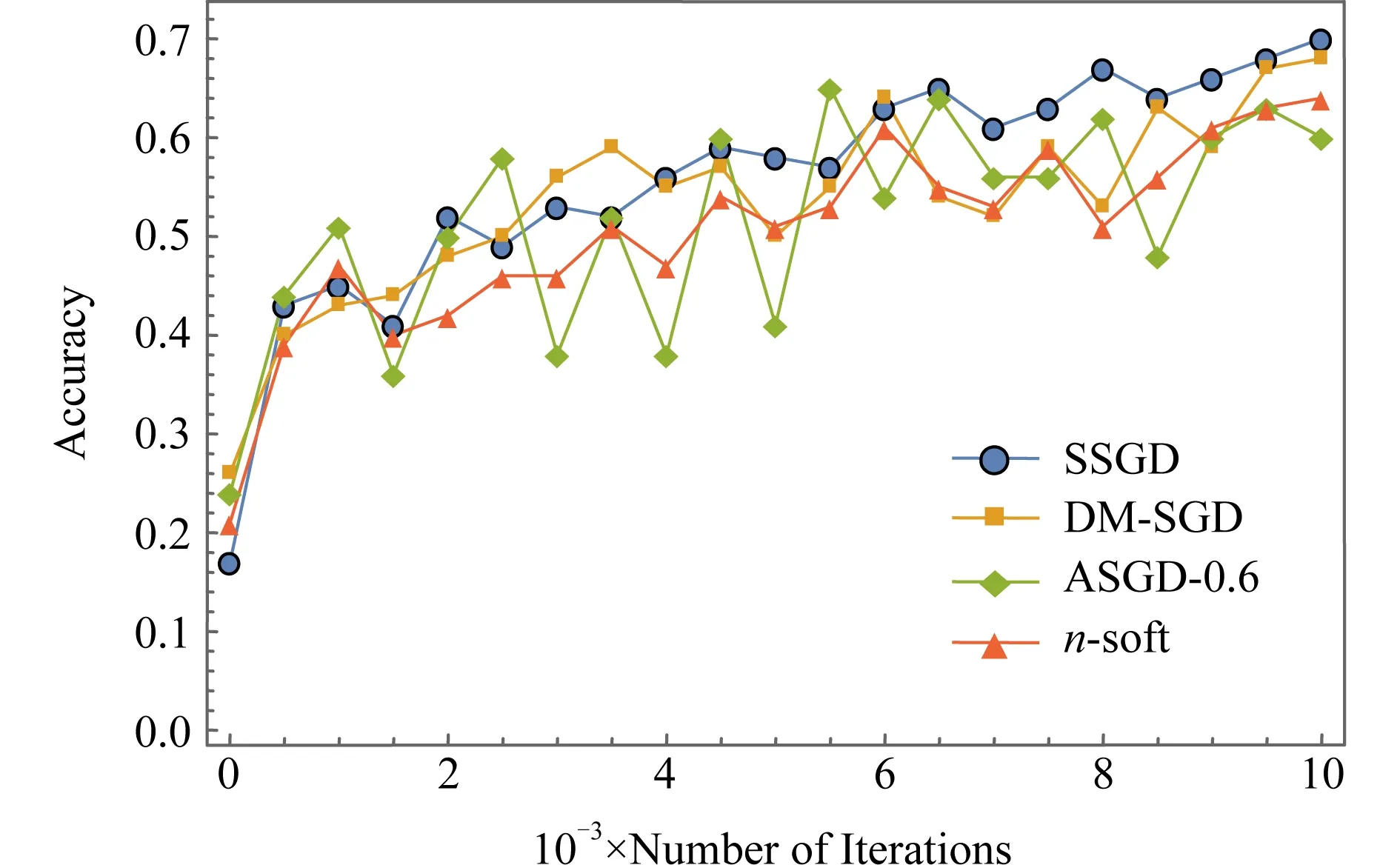

4 结 论

