小学数学建模方法的应用探讨

陈依

数学建模就是建立数学模型解决问题的方法。小学数学建模主要是指在小学数学学习中，用“模型思想”指导数学教学，不断让学生经历从具体事例或现实原型出发逐步抽象、概括地建立起某种模型并解释和运用，从而加深对数学的理解和感受，提升数学学习能力。在小学数学课堂中，如何帮助学生科学、合理、有效地建构数学模型，笔者从以下几方面进行了探讨。

一、借助数形结合，促进数学概念的有效建模

在数学概念的教学过程中，要让学生在充分直观感知的基础上，先将抽象的语言文字转化成图形，然后学会使用抽象的数学符号表达图形，降低学生的思维难度，从而有效地帮助学生理解知识，建构模型。

学生在建立数学模型的过程中，通常要经历三个阶段，即形象——表象——抽象。数学概念教学的核心就是使人明白概念的本质属性。例如，在“百分数的认识”一课中，可以通过出示的信息，开展教学。

1.用流水洗手30 秒以上，可清除80%的细菌。

2.我国最新的调查显示：25%的小学生患近视。

3.第六次人口普查结果，我国男性人口约占51.27%”。从以上例子可以引导学生个性化画图理解80%表示的意思，如：

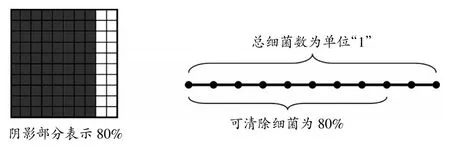
再通过“你是怎样想的？整个方格表示什么？阴影部分表示什么？”“说说你又是怎样表示的？80%是谁与谁比较的结果呢？”等问题的讨论交流，使学生经历并看到用不同的方法表示“清除的细菌是细菌总数80%”。百格图、线段图等表示方法外表有差别，但内在的本质却是相同的——表示两个数在比较，这就帮助学生建立对百分数本质属性的充分感知。然后，再通过对“未清除的占总数的20%”，“25%的小学生患近视”的感知，使学生对百分数的表象逐步清晰起来，最后，水到渠成的抽象出“百分数表示一个数是另一个数的百分之几”这一概念。在这一教学过程中，教师始终围绕“百分数是两个量相比较的结果”这一重点展开，把数与形紧密地结合起来，让学生充分感知，建立表象，抽象概括出概念，促进学生有效地建构起百分数这一模型及其本质的属性。

二、经历建模，优化学生的数据分析观念

小学数学统计与概率的教学，必须注重儿童的日常经验，必须从儿童的生活出发，在儿童充分活动的基础上，在一个具体情境中的活动中去体验、认识和建构。它不要求学生用高深的数学建模知识去解决一些统计和概率问题，而是要通过收集、整理、分析数据等基本统计活动和简单随机现象可能性的探究，逐步从实践的“操作”发展到理论的“建构”，虽然没能使学生系统地掌握建模的方法，但使学生经历了数学建模过程，潜移默化地渗透了数学建模思想。

例如：在“复式条形统计图”的教学中，可以按“点击简单模型——建构复杂模型——完善用活模型”的基本模式展开。单式统计图是复式统计图的原型基础，是学生建模的起点，在课堂一开始通过创设情境，唤起学生对单式统计图的回忆，为建构复式统计图奠定基础。在合并单式统计图的过程中，引导学生动手尝试绘制复式条形统计图，要求是想办法让人一眼就读懂你做的统计图的意思。再依次展示学生的作品并全班交流。

三、重视建模，体验数学应用的价值

“实践与综合应用”中的数学模型就是将问题解决中叙述的生活语言抽象成数学语言，进而转化成数学运算并构建数学模型(数量关系)的过程。一般包括：从现实生活或具体情境中抽象出数学问题，用数学符号和语言表示问题的数量关系和变化规律，求出结果并验证结果。如何重视“实践与综合应用”的建模，笔者结合“搭配规律”这一课例谈几点想法。

1.生活问题数学化，数学解决问题建模的起点

让学生经历将“问题情境”转化成“数学问题”的过程，这样不仅帮助学生理解题意，还是数学建模的起点，为后面的数学建模做好铺垫。

2.用数学语言表达数量关系，建构解决问题的模型

在“搭配规律”一课中，对于搭配问题中数量关系的分析十分重要，要根据学生思维的起点，确定思维的方向，培养学生用数学的语言有序地分析数量关系。教师通过引导学生在变化中寻找不变的思路，认识到用“几个几”的方法能够更好地解决问题，初步抽象出搭配的规律及其背后的数量关系。

3.比较反思，验证数学模型

学生通过对数学问题进行观察、思考、猜测、归纳等一系列的思维活动，初步建立起解决几种不同事物进行有序搭配问题的数学模型，学生虽然解决问题，但对解决问题的过程和方法缺乏数学层面的分析。因此，学生通过在回顾整理、反思比较中不断地建构和调整数学模型。

总之，小学数学建模过程是一个综合性的过程，是数学能力和其他各种能力协同发展的过程。通过建模教学，可以加深学生对数学知识和方法的理解和掌握，调整学生的知识结构，深化知识层次。同时，培养学生运用数学的意识和自主、合作、探索、创新的精神，为学生的终身学习、可持续发展奠定基础。