山区加宽路基挡土墙现场试验及数值模拟分析

冯忠居，王溪清，芦 佳，张晓轴，常应宏

(1. 长安大学 公路学院，陕西 西安 710064； 2. 陕西省榆林公路管理局，陕西 榆林 710009)

0 引 言

近年来，一些学者对重力式挡土墙土压力展开了研究，陈页开等[1]采用数值模拟分析了挡土墙土压力的变化规律；周应英等[2]通过模型试验对土压力分布规律有了新的认识；肖衡林等[3]结合现场试验详细分析了多级重力式挡土墙土压力的时空分布规律；范瑛等[4]对施工阶段多级挡土墙土压力展开研究，并在路基沉降方面也进行了相关研究；傅珍等[5]应用有限元程序开展路基差异沉降的影响性分析，提出了减小差异沉降的设计建议；唐朝生等[6]对路基加宽拼接中的差异沉降进行了数值分析；范红英等[7]针对某公路改扩建工程，建立单、双侧路基拓宽数值分析模型，得到新旧路基位移变化规律；翁效林等[8]通过离心模型试验得出了新、老路基的差异变形特征及处治技术与效果；刘金龙等[9]采用有限元方法，探讨了拓宽路基的基本特性；韩丁等[10]根据实测数据进行参数反演，计算路基顶面差异沉降。公路加宽工程中，在路基填方加宽位置设置挡土墙，既要考虑新、老路基之间的差异变形，还要关注由挡土墙外移而引起的病害，这方面的研究还较少。万智等[11]在考虑支挡结构影响的同时，研究了山区拓宽公路新老路基差异沉降；薛建荣等[12]分析了采用桩网复合地基处理高速公路加宽工程中新老路基差异沉降及路堤拼接质量的问题，证明了其效果良好；蒋鑫等[13]分析了山区公路衡重式挡土墙墙后填土加筋、压实情况下，路基沉降与墙身外倾的影响关系，但未涉及墙后土压力分布的研究。

笔者依托G307改扩建工程，通过现场试验，并借助有限元软件，建立数值分析模型，揭示土压力变化及路基变形规律。将现场试验结果与数值模拟结果对比分析，验证数值模拟的可靠性。并对相关设计及施工参数进行影响性分析，进而用于指导实际工程。

1 现场试验介绍

1.1 试验路段概况

G307吴堡至绥德段改扩建工程的路线穿越地区多为一侧河谷沟槽，另一侧靠山，常以单侧加宽外设挡土墙为主，挡土墙工程在全线所占比例较大，在工程中挡土墙的拼接加宽一般形式如图1。

图1 挡土墙拼接加宽形式Fig. 1 Splicing and widening form of retaining wall

图1(a)为该工程中最为常见的加宽形式，故笔者选取中心桩号K41+890～950拓宽路肩挡土墙工程为试验路段，如图2。试验断面K41+915路基及挡土墙设计参数如下：老路基宽8 m，改线加宽6.2 m，外侧仰斜式路肩挡土墙高5 m，墙背及墙面坡比均为1∶0.25，墙顶宽1.1 m。施工中未进行分层压实，新路基填土可近似分为3层，路基顶面以下：0～1 m为填土1；1～2 m为填土2；2～5 m为填土3，其中，填土3未采用机械碾压。

图2 试验路段Fig. 2 Test section

1.2 试验设计

本试验采用单点沉降计观测新路基土层的沉降变形，布设3处沉降观测点，分别位于设计路中线左2、0 m，右3.5 m；路基土分2层进行观测，自路基顶面以下0.5～2 m范围内为上层，2～5 m范围内为下层。采用压力盒观测挡土墙墙背水平土压力，在墙背布设4个压力盒，每个间距1 m，布设情况如图3。路基顶面以下0～0.5 m为仪器保护层，不考虑该范围内的沉降。

图3 K41+915断面仪器布设(单位：cm)Fig. 3 Instrument layout of K41+915 section

2 有限元模型建立

2.1 几何模型及网格划分

道路为条带形结构物，模型可简化为二维平面应变问题进行分析，以K41+915断面为原型建模，如图4。对网格单元尺寸，首先应细化挡土墙及填方路基的单元尺寸，以保证计算精度，其次控制模型整体单元尺寸上下限，保证不同尺寸之间过渡均匀。试算表明本模型边界效应影响可忽略不计。

2.2 边界条件

计算模型近似为半空间无限体，模型两侧设置水平位移约束，竖直位移自由；模型底部设置水平和竖向位移约束。模型建立完成后添加重力荷载。

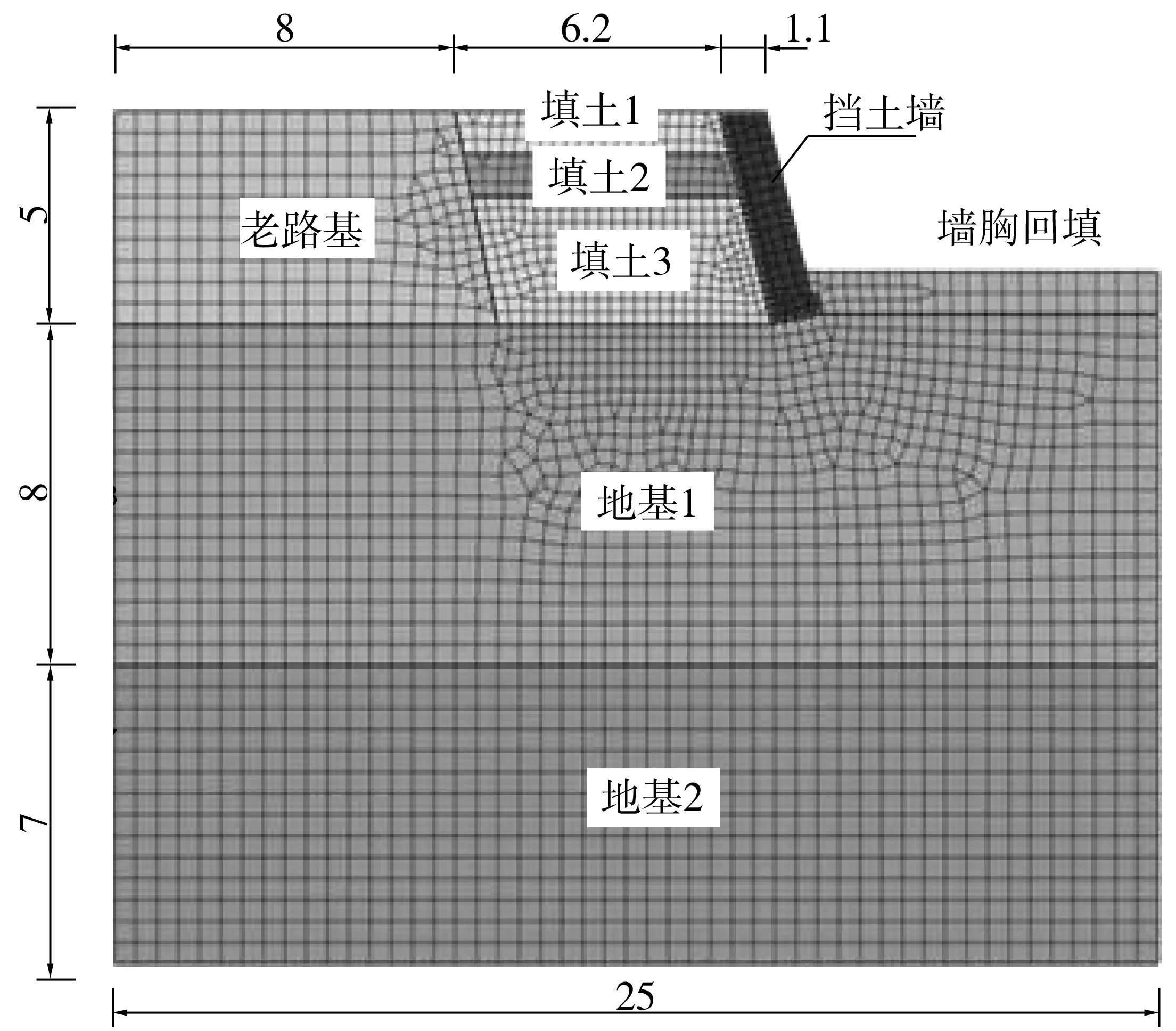
图4 有限元计算模型(单位：m)Fig. 4 Finite element model

2.3 本构模型及计算参数

试验路段挡土墙由浆砌片石砌筑，采用弹塑性本构模型；地基2为岩层，采用理想弹性本构模型；老路基、新路基、墙胸回填土以及地基1视为服从Mohr-Coulomb屈服准则的理想弹塑性材料。根据地勘及设计资料材料参数见表1。由于挡土墙与土体的材料性质差异较大，需在挡土墙与填土及地基之间设置摩擦界面单元，模拟可能出现的相对位移，通过试算[14]界面的法向刚度取4.2×108N·m-1切向刚度取3.8×107N·m-1。

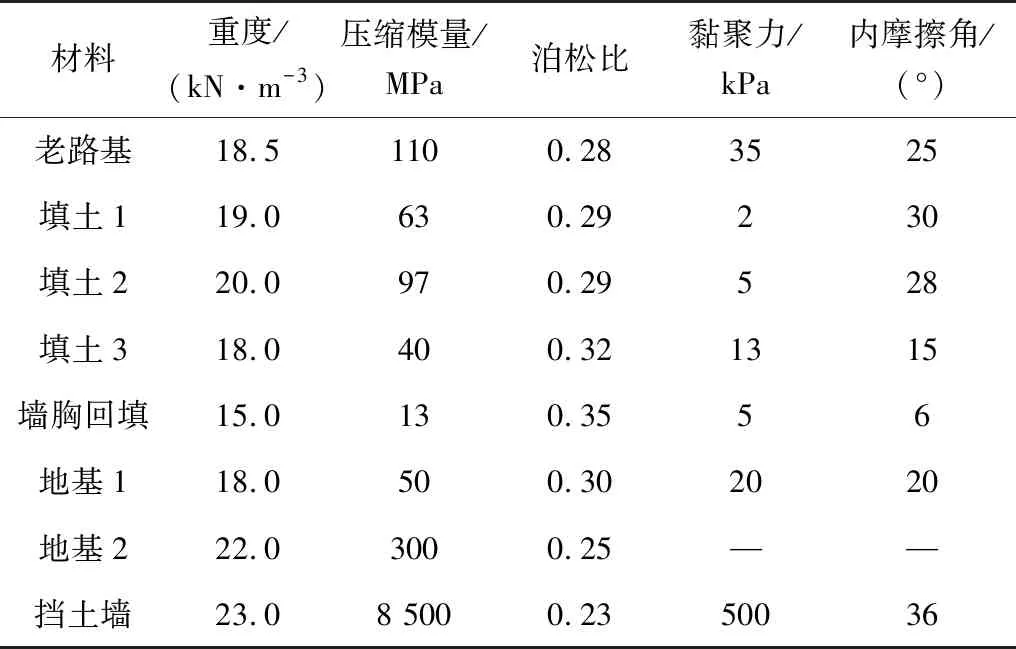
表1 有限元模型计算参数Table 1 Calculation parameters of finite element model

4 施工阶段模拟

分析初始应力状态时，在ANSYS中激活老路基及地基网格单元，并施加边界条件和重力荷载，对初始阶段位移清零，仅考虑工后变形；分析工后应力应变状态时，一次性激活填土、挡土墙等施工网格单元，不考虑分层填筑过程的影响，得到填方土体在自重压密下的位移及挡土墙的应力应变状态，如图5。

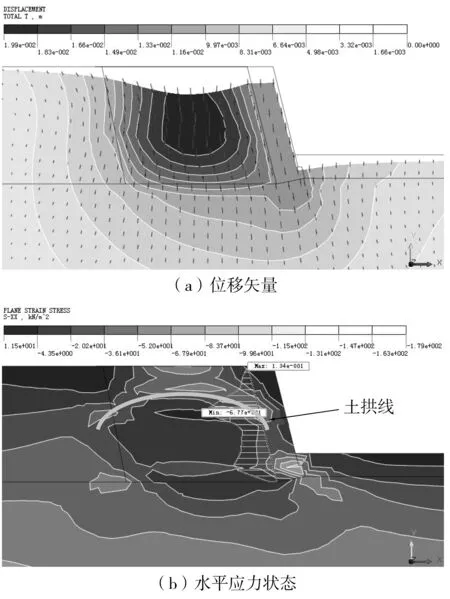
图5 工后路基及挡土墙的应力应变Fig. 5 Stress and strain of subgrade and retaining wall after construction

由图5(a)可知，最大竖向位移位于填方路基形心偏上位置，主要原因是上层填土施工压实度较高，可压缩量较小，而下层填土施工中并未进行分层压实，处于欠固结状态，在自重作用下的竖向变形更多体现在填土3的上表面，而填土与挡土墙之间的相对位移不明显。根据整体变形协调规律，上层填土顶面中部下沉导致两侧土体向中心移动，下层填土顶面受挤压作用，填土由中部向两侧移动，从而使挡土墙下部位移大于上部位移。

由图5(b)可知，填土内部水平应力分布较为复杂，各层填土之间有明显的区域划分，土层中存在土拱效应，即在新路基土层上部存在一条拱形应力集中区域，其产生原因可归结为上、下层土体的刚度差异。

3 试验结果与数值模拟对比分析

3.1 路基沉降

现场试验自挡土墙及新路基填筑碾压完工后进行数据观测，完工后及时测取的数据为初始值，并根据监测频率测得后续数据。在ANSYS中提取该土层顶面、底面竖向位移数据，将两者作差得到数值模拟的沉降数据结果。由此可得实测数据与数值模拟对比，如图6、7。

由图6可知，上层土的沉降在观测期内随时间逐渐增加，道路在中线位置的沉降量相对较大，在478 d的沉降量为2.25 mm；304 d上层土沉降量相对99 d有所减小，2～3 #沉降计的实测值小于初始值，即上层土产生回弹隆起，原因可能是夏季气温升高，路基土体受热膨胀所致。数值模拟结果显示，上层土体沉降量微小，在距老路基中线8 m以上位置，上层土发生回弹隆起，原因可能为上层土底面沉降量大于顶面沉降量。现场实测值大于数值模拟结果，其原因是由于数值模拟结果实为路基土在自重压密作用下的最终沉降，由弹性变形和塑性变形组成，而实际土层仍处于固结沉降阶段，其沉降量会随时间的推移而继续增大，逐渐接近数值模拟结果。

实测下层土道路中线处的沉降增加明显，远大于上层土的沉降量，原因可能为下层土在自重及上部荷载作用下，夹于老路基与挡土墙之间，处于不完全侧限压缩状态，由于土层压实度不足，在中部受力大于两侧的情况下，土体背离中线向两侧移动，中部产生沉陷区，沉降增大明显。数值模拟结果显示下层土最大沉降大致位于土层形心中线，与实测值不同，原因是下层土受挡土墙限制程度与实际情况有所差异，且未考虑车载影响。

图6 上、下层路基沉降对比Fig. 6 Comparison of subgrade settlement in upper and lower layers

图7为路基土层总沉降实测值和模拟值，实测路基在工后测量时差内的最大平均沉降速率分别为0.725、0.024、0.018、0.019 mm/d，99 d之内的沉降速率减小较快，99 d之后基本稳定。478 d实测最大沉降点较模拟值偏左，车载作用影响明显，由2.4分析可知，下层土沉降在路基土沉降中起主导作用。由数值模拟可知，顶面新、老路基交界处差异沉降明显，路基顶面最大沉降值19.22 mm，比路基土层最大沉降值高8.74 mm，地基顶面沉降占路基顶面沉降量的45.47%。

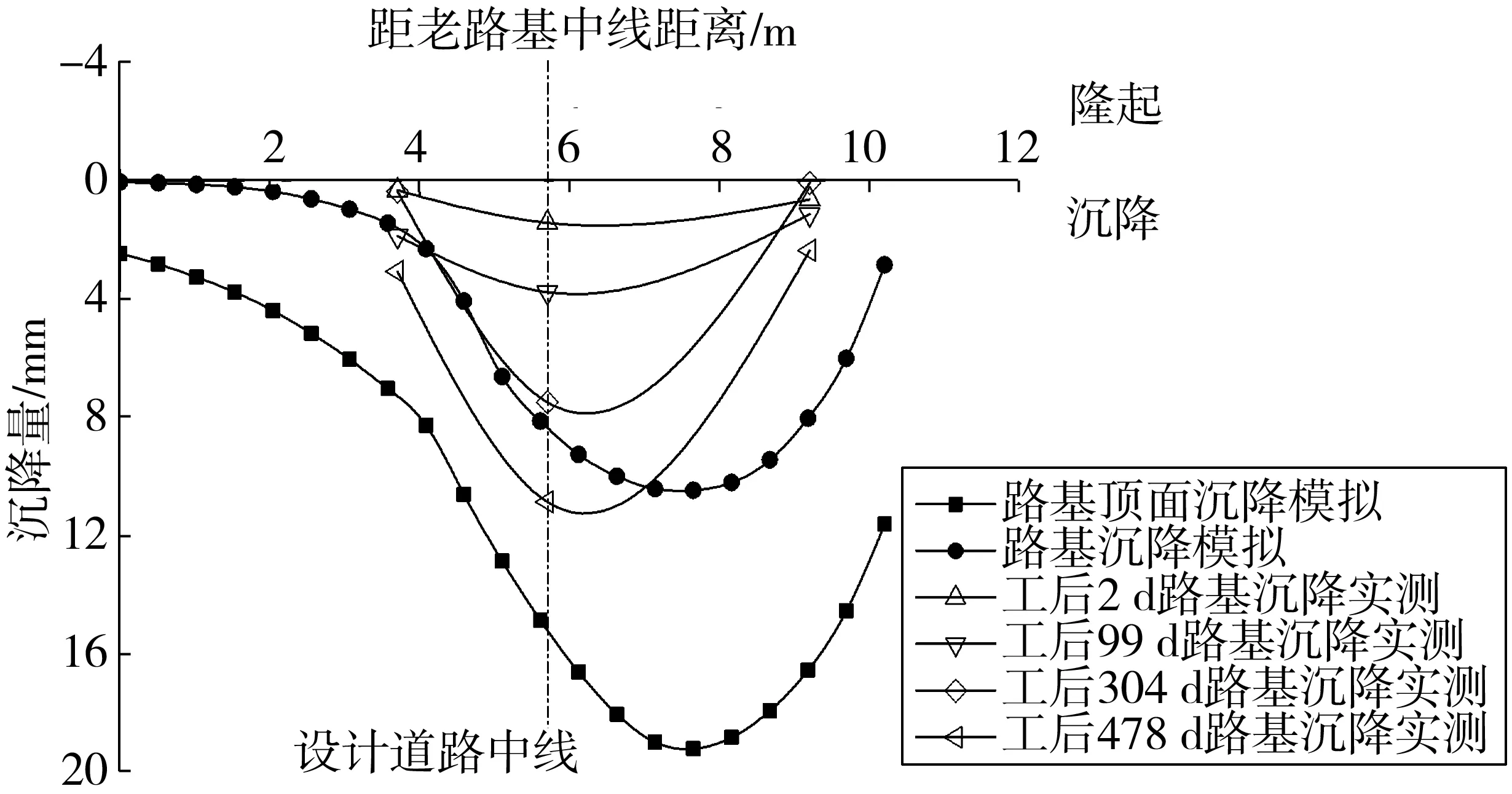
图7 路基土层总沉降Fig. 7 Total settlement of subgrade soil

3.2 挡土墙土压力

根据数值模拟应力计算结果，提取墙背水平应力，同时绘制现场实测土压力分布，如图8。数值模拟结果表明，自墙顶向下土压力有两处突变点，深度2 m处的由土拱效应土压力强度接近70 kPa，深度4.5 m处的土压力突变表现为墙底土压力减小，土拱作用不明显，可能与挡土墙和地基土的刚度差异有关，亦可由于挡土墙底部外移导致压力减小所致。

现场实测值显示，不同时期的土压力分布变化与路基沉降有对应关系。以99～304 d为例，304 d时路基中线两侧沉降点较99 d沉降量变化为负值，即两侧隆起，在上层土中表现明显。2 m深度的土压力强度增大，说明上、下土层交界处土体挤压导致水平应力增大，同时可以解释路基土层沉降负值变化现象。土拱效应对土压力分布变化的影响主要表现为2 m深度处的土压力强度高出正常值，其下部土压力强度小于正常值。

将现场实测值与数值模拟计算结果对比，可以看出，两者具有较高的契合度，数值模拟结果可以较为真实的反应实测断面的应力应变状态。

图8 墙背土压力分布规律Fig. 8 Distribution law of earth pressure on wall back

4 加宽路基挡土墙影响因素分析

为深入探明加宽路基挡土墙的受力与变形特性，采用数值模拟分析方法对填方路基加宽宽度、填方路基弹性模量、老路基边坡坡度以及地基处理深度等因素进行影响性分析，以图4为基本模型，在对某一影响因素分析时，其余参数保持不变。

4.1 不同加宽宽度的影响

山区旧路多环山而建，改扩建工程中旧路基宽度利用存在差异性使填方路基加宽宽度不同，有必要研究加宽宽度变化对路基及挡土墙受力与变形的影响。当加宽宽度分别为4.2、5.2、6.2、7.2 m时，图9给出了土压力分布、墙身水平位移、路基顶面沉降曲线。

由图9可见，在一定宽度范围内，随着新路基加宽宽度增加，路基及挡土墙的变化规律为：墙身上部土压力减小，下部土压力增大，分界点大致位于距墙顶1.5 m处，土压力变化幅度逐渐减弱。随着距墙顶距离的增大，土压力合力及合力矩逐渐增大，但合力作用点降低；由图9(b)可看出，墙底位移逐渐增大，增幅不断减小，加宽宽度大于等于5.2 m时，墙顶位移减小，幅度变化增大；老路基顶面沉降变化不明显，新路基总体沉降量增大，增幅近似，最大沉降点随加宽宽度的增加而逐渐右移，新老路基差异变形逐渐增加，墙身竖向位移所受影响较小。加宽宽度的增加不利于挡土墙及路基的稳定性。

4.2 新路基不同弹性模量的影响

加宽路基填筑材料需要又较高的抗变形能力，合理选择填筑材料可以提高施工质量、降低施工成本。为研究不同材料对路基带来的影响，选取不同的路基弹性模量模拟不同材料的情况。首先定义等效弹性模量Ei(初始值)代表新路基整体弹性模量，各层填土弹性模量按相同比例增大或减小，然后分析不同路基模量下挡土墙土压力、墙身位移及路基顶面沉降变化规律。

图10为新路基弹性模量分别取1/3Ei、2/3Ei、Ei、4/3Ei时的土压力分布、墙身水平位移、路基顶面沉降曲线，可以看出，当新路基填土弹性模量按比例增大时，路基及挡土墙的变化规律：由于弹性模量的取值范围较小，土压力分布变化不明显，土压力合力减小，合力矩降低；墙身整体位移量减小，幅度减弱，墙顶位移变化相对明显；老路基及挡土墙的竖向位移基本不变，填方路基竖向位移量减小，中心点处的位移变化幅度降低。增大一定幅度的弹性模量可以显著降低墙身及填方路基的变形量，故优化填筑材料的选择以及压实指标的控制，可以提高一定的经济效益。

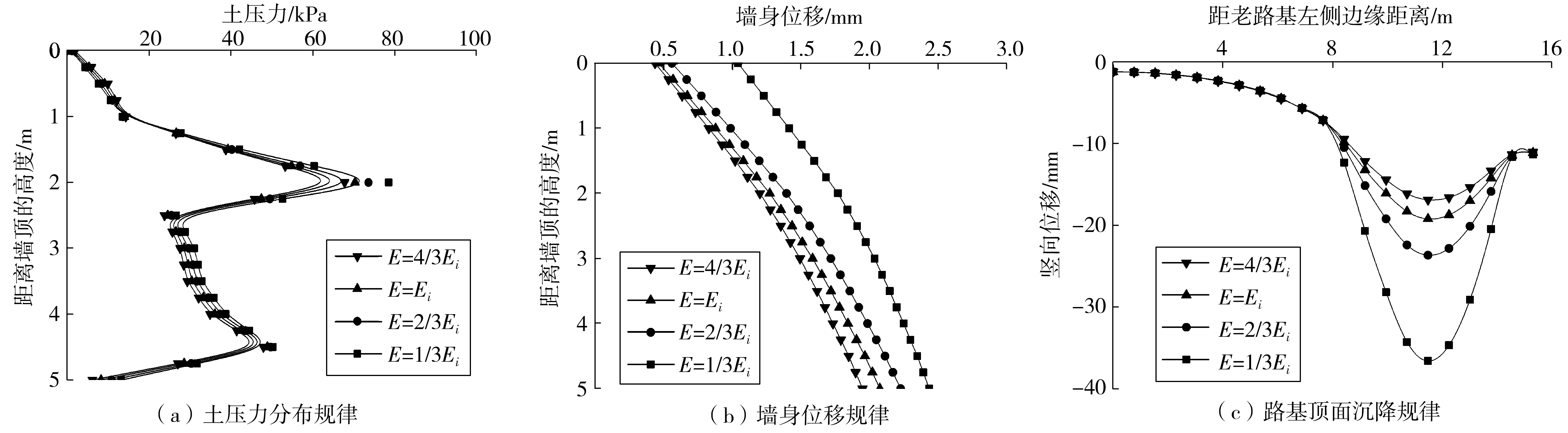
图10 不同弹性模量下的影响Fig. 10 Influence of different elasticity modulus

4.3 老路基不同坡角的影响

山区旧路多穿越陡坡沟壑区域，旧路堤旁沟壑随地形变化起伏，形状不一，因此，对于路基加宽工程，有必要对路基和挡土墙受路堤边坡坡度变化的影响进行研究。由图11可知，当老路基坡角增大时，路基及挡土墙的变化规律：土压力合力增大，合力作用点降低，合力矩增大；墙底位移随老路基坡角的增大而增加，增幅逐渐减小。墙顶位移的变化规律与墙底相反；填方路基沉降随着老路基坡角的增大而增大，老路基右侧沉降也随之增加，新老路基差异沉降减小。因此，减少老路基边坡土体的开挖，有利于提高挡土墙和路基的稳定性。

图11 不同老路坡角的影响Fig. 11 Influence of different slope angles of old road

4.4 不同地基处理深度的影响

山区填方加宽路基多置于旧路旁沟壑之中，沟壑土体含水量高，强度低，一般采用换填法进行处理，合理深度的地基处理可以改善路基及挡土墙的工作性能。数值分析中，通过调整新路基及挡土墙下部地基土体参数(压缩模量E=60 MPa；黏聚力c=5 kPa；内摩擦角φ为30°)模拟地基处理。由图12可见，随着地基换填处理深度的增加，墙身土压力分布基本不变；墙身位移随着地基换填处理深度的增加显著减小，处理深度的增加对墙底位移量的影响相对明显；随着地基换填处理深度增加，新路基和挡土墙的相对竖向位移基本不变，总体沉降变化较小。因此，对地基进行一定深度的换填处理，可以减小墙身水平位移量，但对改善土压力分布和路基差异沉降的效果并不明显。

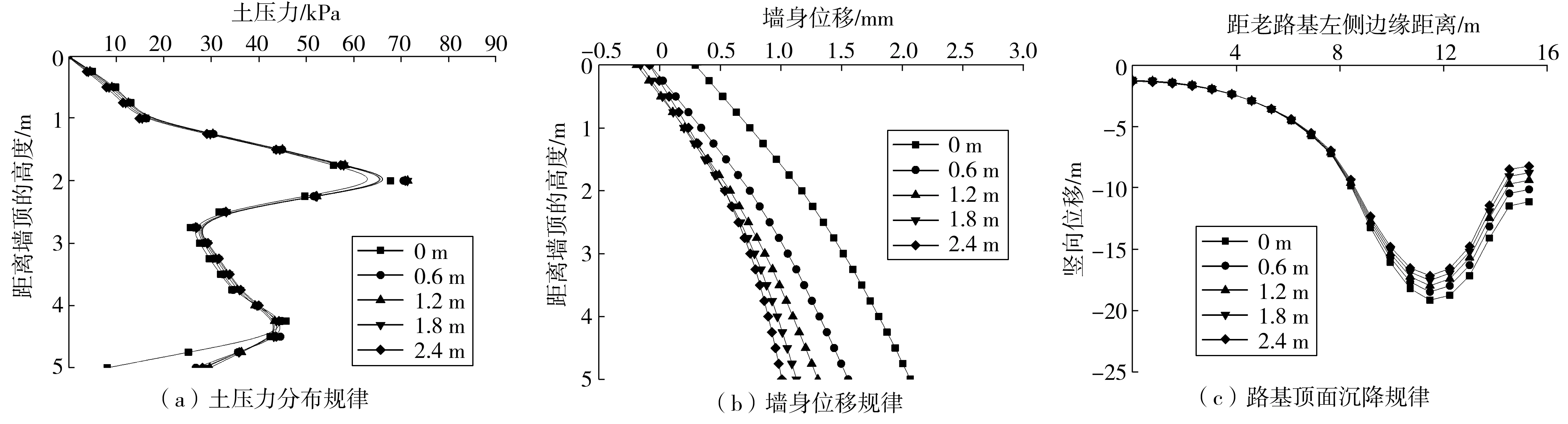
图12 不同地基处理深度的影响Fig. 12 Influence of different foundation treatment depth

5 结 论

1)由于土层刚度的差异，填方路基最大沉降点大致位于下层土上表面中心，上层土沉降量相对较小，土层中存在土拱效应。需注重控制各层填土的压实指标。

2)实测路基土层设计路中线处的总沉降量最大，路基土层最大沉降模拟值位于填方土体形心中线，可解释为在一定时间限度内，车载作用较土层固结的影响度高。下层土沉降在路基沉降中起主导作用。

3)土拱效应对土压力分布变化的影响主要表现为2 m深度处的土压力强度高出正常值，其下部土压力强度小于正常值。土压力的变化与路基变形的关系密切。

4)在一定宽度限制内，随着加宽宽度的增加，路基的稳定性降低；提高一定的填方土体整体压实度或改善填料性质，可以较大幅度的改善路基及挡土墙的变形特性，可通过试验确定最优方案；控制老路基边坡土体的开挖，有利于提高挡土墙和路基的稳定性；对地基进行一定深度的换填处理，可以减小墙身水平位移量。