试卷讲评教学中“滑过现象”的思考与浅析
☉江苏省太湖高级中学 浦丽敏
涵盖大量知识点且知识跨度较大的试卷讲评教学中极易产生“滑过现象”,教师在试卷讲评中要突出一些关键问题和环节,给予学生足够的探究空间以避免“滑过现象”的产生并引领学生在问题的探索与思考中获得思维与兴趣的不断提升.
一、何谓滑过现象
车速太快往往会导致路边的“美景”在驾驶者眼中“一滑而过”,驾驶者滋生惰性、麻痹心理的同时也更易发生事故,这种生活中的“滑过现象”在高中数学教学过程中也有类似的存在.过于简单或平铺直叙、就题论题的问题设计往往无法激发学生的深入思考,再加上教学进度过快等因素,学生亲身体验、感悟的机会急剧减少并造成具备探索价值的内容在教学过程中的无意“滑过”,这种“滑过现象”在高三试卷讲评教学中是最容易产生的,这种课型往往会涵盖大量的知识点,知识内容上的跨度和新授课相比也明显更大,部分学生因为自己的解题正确也会在课堂上更显懒惰而导致很多精彩的问题在我们面前“一滑而过”.因此,高中数学教师一定要遵循教学的基本原理并着眼于问题的本质进行教学的落实,引导学生对问题隐藏的价值进行探究并努力使问题能够更好地为学生所关注.学生这一学习的主体“做数学”应该是数学学习中最为重要的环节,教师在试卷讲评中一定要突出一些关键问题和环节,给予学生足够的探究空间,并引领学生在问题的探索与思考中获得思维与兴趣的不断提升.
二、典型案例
1.试题讲解
引例已知抛物线C,其顶点与原点重合,焦点为F(0,1).
(1)抛物线C 的方程如何?
(2)抛物线C 上是否存在一点P 使过点P 的直线与抛物线C 交于点Q,满足PF⊥QF,且PQ和抛物线C 在点P 处的切线垂直?若存在,点P 坐标如何?若不存在,理由何在?
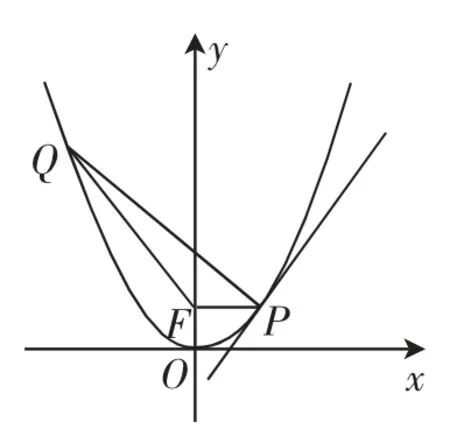
图1
解析:(1)抛物线C 的方程易求,方程为x2=4y.
(2)设P(x1,y1),Q(x2,y2),则抛物线C 在点P 处的切线方程为,直线PQ 的方程为将其代入抛物线C 的方程即可得出则.所以又因为·(y2-1)=x1x2+y1y2-(y1+y2)+1=0,
点评:这是一道能够全面考查学生运算与思维能力的好题,富含抛物线的切线、法线等知识的这一好题值得探究,问题的轻易“滑过”是不可取的.
三、例题本质的剖析
圆锥曲线的对称、统一、简明给人优美的感觉和无穷的想象空间,站在一定的高度对圆锥曲线问题进行审视,我们能够透过现象看到本质并弄清问题的来龙去脉.
一般化:已知抛物线C:x2=2py(p>0)上有一点P,过点P 的直线与C 的交点为Q,F 为其焦点,若PF⊥QF 且PQ 和C 在点P 处的切线l 垂直,则点P 为定点.

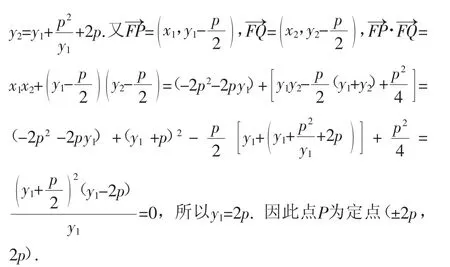
引申1:已知抛物线C:x2=2py(p>0)及其焦点F,点P(2p,2p)在抛物线上,过点P 的直线与抛物线C 相交,交点记作Q,如果PQ 和抛物线C 在点P 处的切线l 垂直,则PF⊥QF.
证明:抛物线C 在点P(2p,2p)处的切线l 的方程为y=2x-2p,因此直线PQ 的方程为,代入x2=2py 即可得出x2+px-6p2=0,根据根与系数的关系可得xPxQ=-6p2,因此.所以.故,问题得证.
引申2:已知抛物线C:x2=2py(p>0)及其焦点F,点P(2p,2p)为抛物线C 上一点,过点P 的直线与抛物线C相交,交点为Q,若PQ 和抛物线C 在点P 处的切线l 垂直,设切线l 和x 轴的交点为R,则∠RPF=∠PQF.
点评:引申2 其实是在引申1 的基础上作出的变式,由引申1 可知PF⊥QF.因此∠RPF=∠PQF.在结构特征上表现得与圆的弦切角定理特别相似,引申2 可以说是圆的弦切角定理在抛物线中的推广.
引申3:已知抛物线C:x2=2py(p>0)及其焦点F,点P(2p,2p)为抛物线C 上一点,过点P 的直线与抛物线C相交,交点为Q,抛物线C 在点P 处的切线记作l,若PF⊥QF,则PQ⊥l.
证明:抛物线C 在点P(2p,2p)处的切线l 的方程为y=2x-2p,直线PQ的方程为y-2p=k(x-2p),代入x2=2py,得x2-2pkx+4p2k-4p2=0.由根与系数的关系可得xP+xQ=2pk.因此xQ=2pk-2p.所以,即所以.因此PQ⊥l,命题得证.
对一道题进行剖析、引申并挖掘其深层次的知识点不仅能帮学生夯实基础,还能将知识点进行由点及面的拓展.知识与问题在学生面前都变得鲜活而有生命力,学生在多角度的思考中也使思维的辐射面更广,视野与思维均得到了拓展.
四、滑过现象的思考
教学过程中“滑过现象”的产生主要是因为教师对学生思维认识的偏差.很多教师因为高三学习时间紧,将试卷讲评变成了对答案而致使很多鲜活的探究素材流失.再加上教师在教学中不能将自己的教学所思与设计放在学生“悟”的过程中,“滑过现象”就此产生.另外,有的教师往往着眼于预防学生犯错而落实教学,这种教学思路与预设往往导致学生体验犯错与纠错的机会轻易滑过.事实上,学生在错误中的体验,对其深层理解问题的本质也是极其重要的经历.
教师在学生的学习生涯中扮演着学生生命发展激活者的角色,教师与学生在课堂对话过程中全身心地投入互动,能使教师和学生的生命在数学活动中涌动与成长,数学课堂也会因为师生生命的多方向发展而焕发生命的活力.因此,教师在新课标理念的引领下落实具体教学时一定要关注学生的体验,以及教学的形式、过程与效果.
教师在新课程理念的引领下由知识的传授者转变成了学生学习的组织者与引领者,这意味着课堂教学活动的中心也转移到了学生的“学”上.因此,教师应在课堂上创设出和谐民主的情境与学习氛围,使学生在轻松的氛围中对问题展开充分的思考和探索.教师在关键问题与环节的处理上应给予学生充分的空间并积极引导学生在自主参与中对问题形成感悟,使学生能够在获得知识的同时体验成功.因此,教师应引导学生克服思维惰性并积极主动探索以防止滑过现象的产生.精心设计能够凸显“数学本质”的探究活动并使学生在亲身经历中有所发现、展开探索,使学生在充分感受知识的形成过程中获得深刻的体会与灵动的思维.与此同时,教师还应注意问题设计的坡度,坡度太小的问题设计往往会使学生的思维产生惰性,很多具备一定探究价值的素材也会因此在教师与学生面前“一滑而过”;坡度太大的问题设计往往会超出学生的能力范围,学生的探究会因此流于形式而不达根本,这种事实上的滑过现象也是教学的缺憾.总之,教师应认真领会课改精神并对教学要求展开细致的研究,使学生在精心设计的问题情境中展开探索和猜想,使学生获得更为广阔的自主探索的空间,使学生的个性品质、学习能力均得到和谐发展.

